The Quantum String: Direct Solution of the Schrodinger Equation

A wave function in an infinite square well is similar in some respects to a classical string clamped at both ends. Both can be started off in a pluck or pulse configuration, both have their change in configuration driven by their curvature, and since both obey zero boundary conditions, their time evolution can generated using the FFSS. The Schrodinger equation differs from Newton's law in two important ways: it involves a first time derivative instead of a second, and the square root of -1 appears explicitly in it. As a consequence, we cannot solve it using the Feynman algorithm (although we will use a half-step look ahead), and we have to keep track of real and imaginary parts (the curvature in one drives the time dependence of the other). We can put the equation into suitable form for numerical solution by introducing the period of the lowest energy stationary state:

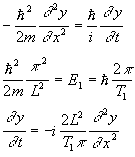
The only parameters in the final form of the equation are the width L of the well and the ground state period. We can predict the period of the quantum mechanical oscillation using our knowledge of the FFSS and the fact that the stationary states have periods that are inversely proportional to their quantum numbers. The pluck and pulse displacements involve only odd terms in their FFSS, so

Terms in the FFSS that are in phase initially will again be in phase one eighth of the ground state period later. We use this information here only to help in choosing a suitable time step and range. The program divides the oscillation period into 128 plotting frames with 100 time steps between each frame. The calculation uses a half-step look ahead similar to what we used in field plots: we want the curvature in the function at the mid-point of the time step we are about to take. The program plots the probability density (the sum of the squares of the real and imaginary parts of the wavefunction), and the final plot is compared with the initial one.

The agreement with the initial plot is not particularly good, but there is no point in attempting to refine the numerical procedure when the FFSS solution readily available. Our objective in the direct solution was mainly to "demystify" the time-dependent Schrodinger equation. Note that the half-step look ahead is absolutely necessary. We cannot demonstrate how effective the look ahead is because without it the solution blows up.