Rechnerarithmetik

Zahlensysteme
Die allgemeine Darstellung für den Wert $W$ einer Zahl in einem beliebigen Zahlensystem mit der Basis $B$, den Ziffern $a$ und den Stellenwerten $B^{k}$ kann durch folgende Gleichung ausgedrückt werden:

$$W = \sum_{k=-m}^{n} a_{k} B^{k}$$ (1)

mit $0 \leq a_{k} \leq B-1$. $m$ gibt hierbei die Anzahl der Nachkommastellen an, $n+1$ ist die Anzahl der Stellen vor dem Komma. Man unterscheidet im wesentlichen zwischen 4 Darstellungen, dem Dualsystem mit $B=2$, dem Oktalsystem mit $B=8$, dem Dezimalsystem mit $B=10$ und dem Hexadezimalsystem mit $B=16$. Die eigentliche Zahl wird dann einfach durch Angabe der Ziffern $a_{k}$ dargestellt. So können wir die Dezimalzahl 1989 schreiben als

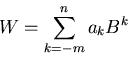11111000101	im Dualsystem
3705	im Oktalsystem
1989	im Dezimalsystem
7C5	im Hexadezimalsystem

Im Hexadezimalsystem werden die Ziffern 10 bis 15 durch die alphabetischen Zeichen A bis F ersetzt.

Dualsystem
Ein Digitalrechner kann nur mit den Ziffern 0 und 1 rechnen. Dieses wird dadurch realisiert, daß eine elektrische Größe wie Spannung oder Magnetfeld entweder an oder aus ist. Dieses führt zwar zu einer ungeheuren Verschwendung von Schaltelementen, ergibt aber andererseits eine außerordentliche hohe Rechengenauigkeit. An oder aus heißt hierbei einfach, daß die elektrische Größe oberhalb oder unterhalb einer bestimmten Schwelle liegen muß. Wie weit sie oberhalb oder unterhalb liegt, ist belanglos. Systeme, die nur zwei stabile Betriebszustände einnehmen können, werden als Binärsysteme (zweiwertige Systeme) bezeichnet. Ein Wechsel des Signals von 0 auf 1 stellt in seinem Informations- oder Nachrichteninhalt eine Elementarentscheidung zwischen zwei entgegengesetzten Werten (vorhanden - nicht vorhanden, falsch - richtig, ja - nein) dar. Es ist klar, daß es belanglos ist, welche der Informationen man mit 0 oder 1 bezeichnet. Diese Informationsmenge bezeichnet man als Nachrichteneinheit $NE$ oder, als Abkürzung für den englischen Ausdruck binary-digit, als bit. Aus der 4. Grundaufgabe der Kombinatorik können wir sofort herleiten, daß man mit $n$ bits $2^{n}$ Binärkombinationen realisieren kann, also auch $2^{n}$ Zahlen (oder allgemeiner Zeichen) darstellen kann. Umgekehrt können wir auch fragen, wieviele Binärstellen werden benötigt, um eine bestimmte Informationsmenge durch Binärkombinationen darzustellen. Hierzu definieren wir zunächst den binären Logarithmus als Umkehrfunktion der Potenz zur Basis 2.

$$2^{n}=x \rightarrow ld(x) = n.$$ (2)

Man kann den binären Logarithmus ausdrücken durch den dekadischen Logarithmus:

$$ld(n) = 3.32 \; log(n).$$

Es gilt dann der Satz:
Satz: Zur Darstellung von n Zeichen oder Zahlen werden mindestens $x = ld(n)$ bits benötigt.
Als Beispiel betrachten wir das lateinische Alphabet mit 26 Buchstaben. Wir erhalten $ld(26) = 3.32 \; log(26) = 4.7 bit$. Technisch lassen sich aber nur ganze Binärstellen realisieren, da die elementare Nachrichteneinheit bit nicht mehr unterteilbar ist. Damit sind für die binäre Darstellung des Alphabets 5 bits bzw. 5 Binärstellen erforderlich. Mit 5 bits könnte man aber eigentlich $2^{5}=32$ Zeichen darstellen, den Überschuß von 6 Binärkombinationen bezeichnet man als Redundanz.

Rechnen mit Dualzahlen
Die Rechenregeln der arithmetischen Algebra sind unabhängig vom Zahlensystem. Die Operationen der allgemeinen Algebra, wie Addition, Subtraktion, Division und Multiplikation, die wir vom Dezimalsystem her gewohnt sind, lassen sich daher auch auf Dualzahlen anwenden. Die Grundregeln für die Addition mit den binären Zahlen 0 und 1 sind die folgenden:

$$\begin{array}{ccl} 0 + 0 &=& 0 \\ 1 + 0 &=& 1 \\ 0 + 1 &=& 1 \\ 1 + 1 &=& 0 \; mit \; ''Ubertrag \; 1 \end{array}$$

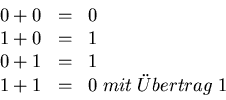
Die folgenden Rechenbeispiele werden jeweils parallel mit dezimalen und dualen Zahlen durchgeführt.

dezimal		dual
10	Übertrag	110000
25	Summand	11001
+28	Addend	+ 11100
53	Summe	110101

Die entsprechenden Rechenregeln für die Subtraktion sind:

$$\begin{array}{ccl} 0 - 0 &=& 0 \\ 1 - 1 &=& 0 \\ 1 - 0 &=& 1 \\ 0 - 1 &=& 1 \; mit \; Entlehnung \; 1 \end{array}$$

Bei 0 - 1 muß eine 1 von der nächsthöheren Stelle geborgt werden (Entlehnung). Wir zeigen wieder ein kleines Rechenbeispiel:

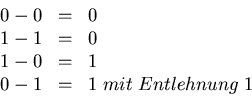
dezimal		dual
25	Minuend	11001
-18	Subtrahend	-10010
-10	Entlehnung	- 1100
07	Differenz	00111

Die Subtraktion wird in Digitalrechnern immer auf die Addition zurückgeführt. Die Subtraktion von zwei dreistelligen Dezimalziffern kann man wie folgt schreiben:

$$A - B = A + (999 - B) - 1000 + 1$$

In der Klammer steht hierbei das sogenannte Komplement auf 9. Jede Ziffer des Subtrahenden wird auf die Zahl 9 ergänzt. Diese Ergänzung auf 9 ist im eigentlichen Sinne keine Subtraktion, sondern eine formale Abbildung, die man in Form einer kleinen Tabelle speichern kann. Es tritt nämlich keine Entlehnung auf. Man verfährt also in folgenden Schritten: 1. Bilde vom Subtrahenden das 9-er Komplement; 2. addiere dazu den Minuenden; 3. zum Ergebnis eine 1 hinzuaddieren; 4. die 1 in der höchsten Resultatsstelle ist zu streichen. Die verbleibende Zahl ist das gesuchte Ergebnis.

Für Dualzahlen läßt sich das gleiche Verfahren anwenden. Allerdings müssen wir jetzt vom Subtrahenden das Komplement auf 1 bilden. Dieses 1-er Komplement ist rechentechnisch besonders einfach, man muß lediglich jede Bitstelle einzeln negieren. Das obige Beispiel der Dezimalzahlen 25 - 18 möge dieses verdeutlichen:

1. Schritt	2. Schritt	3. Schritt	4. Schritt
1-er Komplement	+ Minuend	+1	Streiche höchste Stelle
11111	01101	100110
-10010	+11001	+000001
01101	100110	100111	00111

Die Subtraktion wird also ersetzt durch eine Addition des komplementierten Subtrahenden und des Minuenden.

Wir müssen noch den Fall diskutieren, wenn der Subtrahend größer ist als der Minuend. Bekanntlich erhält man in diesem Fall ein negatives Ergebnis. Dieses läßt sich mit folgender Regel behandeln: Ist der Minuend kleiner als der Subtrahend, so wird zum Minuenden das 9-er (1-er) Komplement des Subtrahenden hinzuaddiert, und das so erhaltene Ergebnis zurückkomplementiert. Ein Dekadenübertrag in der werthöchsten Stelle tritt nicht auf. Ein Beispiel möge diese Regel belegen. Gesucht ist die Differenz 48 - 89 im Dezimal- bzw 11101 - 10110111 im Dual- System.

	dezimal	dual
$B$	89	10110111
$K_{B}$	10	01001000
$+A$	+48	+00011101
$=K_{D}$	58	01100101
$D$	-41	-10011010

Die Multiplikation von Dualzahlen wird exakt wie bei Dezimalzahlen durchgeführt. Das ,,kleine Ein-mal-Eins'' (daher der Name) ist

$$\begin{array}{ccc} 0 \cdot 0 &=& 0 \\ 0 \cdot 1 &=& 0 \\ 1 \cdot 0 &=& 0 \\ 1 \cdot 1 &=& 1 \end{array}$$

Das Rezept für die Multiplikation erinnern wir mit dem folgenden Beispiel:

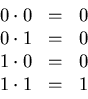
dezimal

25 $\cdot$ 18

200

250

450

dual

11001 $\cdot$ 10010

110010

110010000

111000010

Im Beispiel der Dualzahlen wurden alle trivialen Reihen, die nur Nullen enthalten, weggelasen. Das Bilden der Teilprodukte und deren stellenrichtige Verschiebung ist ein rein formaler Vorgang. Er kann schaltungstechnisch durch Schieberegister realisiert werden. Daher wird letzten Endes auch die Multiplikation von Dualzahlen auf eine Reihe von hintereinander ausgeführten Additionen zurückgeführt.

Bei der Division wird geprüft, wie oft der Divisor im Dividenden enthalten ist. Das Ergebnis erhält man durch wiederholte Subtraktion des Divisors. Folglich können alle Rechenoperationen im Dualsystem in einfacher Weise auf die Addition zurückgeführt werden.

Elektronische Addierwerke
Die Rechenregeln der Addition können in der folgenden Funktionstabelle zusammengefaßt werden (U = Übertrag, S = Summe):

A	B	U	S
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

Die disjunktiven Normalformen ergeben sich zu:

$$U = A \cdot B , \; \; \; \; S = (\overline{A} \cdot B) + (A \cdot \overline{B})$$

Eine schaltungstechnische Realisierung aus NAND Verknüpfungen kann man durch folgende Umwandlung der vorherigen Gleichungen erreichen (der Leser möge diese Umwandlung nachrechnen) (siehe Abb.1).

$$U = \overline{\overline{A \cdot B}}, \; \; \; \; S = \overli... ...ot B)}]} \cdot \overline{[B \cdot \overline{(A \cdot B)}]} }$$

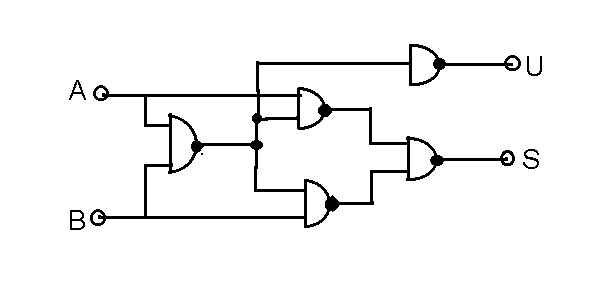
Abbildung 1: Schaltung eines Halbaddierers aus NAND- Verknüpfungen.

Diesen Addierer nennt man auch einen Halbaddierer. Halbaddierer deshalb, weil er keinen Übertrag aus einer wertniedrigeren Stelle verarbeiten kann. Im folgenden Applet können Sie mit diesem Halbaddierer spielen. Das Applet selbst haben wir in einer früheren Lektion bereits diskutiert. Einen 1-bit Volladdierer erhält man durch Zusammenschalten zweier Halbaddierer. Eine Schaltung zeigt Abb.2 und eine Realisierung aus NAND und NOT Elementen ist im folgenden Applet angegeben.

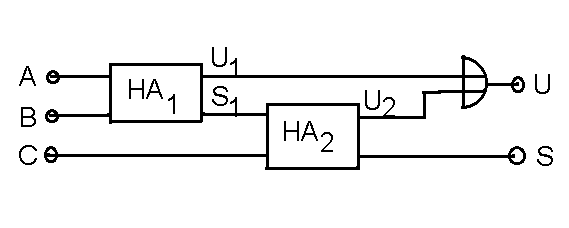
Abbildung 2:Schaltung eines 1-bit Volladdierers aus 2 Halbaddierern.

Die Funktionsgleichungen und die Funktionstabelle (siehe Tabelle 1) dieses Volladdierers sind wie folgt:

$$\begin{array}{ccl} S &=& (S_{1} \cdot \overline{C}) + (\overl... ...) \\ U &=& U_{1} + U_{2} = U_{1} + (S_{1} \cdot C) \end{array}$$

Tabelle 1:

$C$	$A$	$B$	$S_{1}$	$U_{1}$	$U_{2}$	$U$	$S$
0	0	0	0	0	0	0	0
0	0	1	1	0	0	0	1
0	1	0	1	0	0	0	1
0	1	1	0	1	0	1	0
1	0	0	0	0	0	0	1
1	0	1	1	0	1	1	0
1	1	0	1	0	1	1	0
1	1	1	0	1	0	1	1

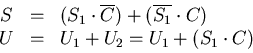
Mit diesem 1-bit Volladdierer kann jetzt ein Dual- Addierwerk beliebiger Stellenzahl (n-bit Addierer) aufgebaut werden. Hierbei wird jeweils der Übertrag $U_{i}$ aus der wertniedrigeren Stelle $i$ auf den Eingang $C_{i+1}$ der werthöheren Stelle geführt (siehe Abb.3).

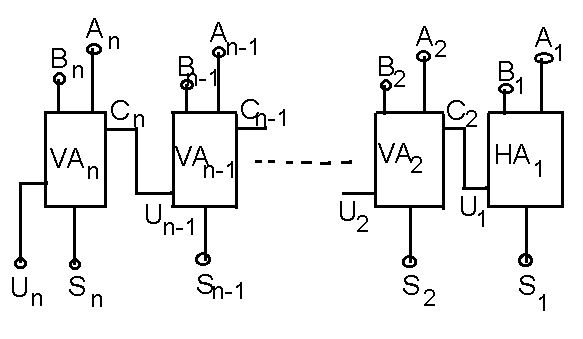
Abbildung 3: Schaltung eines n-bit Addierers aus (n-1) 1-bit Volladdieren und einem 1-bit Halbaddierer.

Die wertniedrigste Stelle braucht natürlich nur als Halbaddierer ausgeführt zu sein, da kein Übertrag aus einer noch niedrigeren Stelle als Eingangsgröße vorhanden ist. Mit Hilfe eines ähnlichen Verfahrens kann man auch Subtrahierwerke entwickeln. Wir werden darauf jedoch nicht weiter eingehen, da in digitalen Rechenanlagen immer eine Subtraktion auf eine Addition zurückgeführt wird. Das Verfahren wurde bereits ausführlich diskutiert. Wir formulieren noch einmal die allgemeine Subtraktionsregel:
Eine Subtraktion wird als Addition durchgeführt, indem der komplementierte Subtrahend zum Minuenden addiert wird. Ensteht dabei in der werthöchsten Stelle der Übertrag 1, so ist das Ergebnis eine positive Zahl, sie muß aber noch um 1 vergrößert werden (Korrekturaddition). Entsteht in der werthöchsten Stelle hingegen der Übertrag 0, dann ist das Ergebnis eine negative Zahl, sie muß dann noch zurückkomplementiert werden.

Im folgenden Applet zeigen wir einen 4-bit Volladdierer und Subtrahierer. Hierzu haben wir in der Palette ganz unten einen integrierten 1 bit Addierer hinzugefügt. Das Schaltzeichen für diesen umschaltbaren Addierer/Subtrahierer haben wir neu erfunden und ist in der Abbildung links gezeigt. Der unterste Eingang M dient zum Umschalten vom Addierer zum Subtrahierer. Die beiden anderen Schaltzeichen rechts in der Abbildung sind übliche Zeichen für einen Volladdierer.

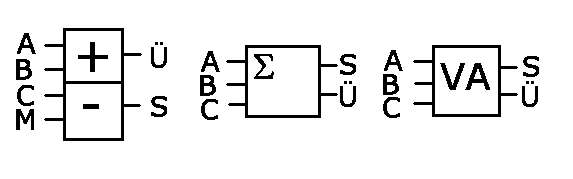
Rechnerarithmetik
Digitalrechner arbeiten im allgemeinen mit n=16 oder n=32 bit Zahlendarstellung. Negative Zahlen werden hierbei immer bereits als komplementierte Zahlen gespeichert, d.h. negative Zahlen erkennt man an einer 1 in der werthöchsten Stelle. Für die eigentliche Zahlendarstellung verbleiben lediglich 15 oder 31 bits. Hiermit kann man die positiven Zahlen von 0 bis $2^{15}-1$ = 32767 bzw. bis $2^{31}-1$ = 2147483647 darstellen. In vielen modernen Rechenanlagen wird allerdings nicht das Komplement selbst gespeichert, sondern das Komplement plus der Korrekturaddition. Dieses nennt man auch das 2-er Komplement. Diese beiden Darstellungen negativer Zahlen werden in der folgenden Tabelle verglichen, am Beispiel eines 16 bit Rechners.

Tabelle 2:

Oktalzahl	Dualzahl	Dezimalzahl	Dezimalzahl
		(1-er Kompl.)	(2-er Kompl.)
077777	0 111 111 111 111 111	32767	32767
077776	0 111 111 111 111 110	32766	32766
077775	0 111 111 111 111 101	32765	32765
.....
000010	0 000 000 000 001 000	8	8
000007	0 000 000 000 000 111	7	7
......
000001	0 000 000 000 000 001	1	1
000000	0 000 000 000 000 000	0	0
177777	1 111 111 111 111 111	-0	-1
177776	1 111 111 111 111 110	-1	-2
.....
177771	1 111 111 111 111 001	-6	-7
177770	1 111 111 111 111 000	-7	-8
177767	1 111 111 111 110 111	-8	-9
.....
100001	1 000 000 000 000 001	-32766	-32767
100000	1 000 000 000 000 000	-32767	-32768

Wir haben in diesem Beispiel auch die Oktalzahlen angeschrieben, da sie wesentlich kürzer sind als die Dualzahlen, und man aus ihnen das Bitmuster ebenfalls sofort ablesen kann. Die Anzahl der darstellbaren Zahlen ist im 2-er Komplement um eins größer als im 1-er Komplement. Dafür gibt es im 1-er Komplement 2 Nullen, eine positive und eine negative. Der Vorteil der Zahlendarstellung im 2-er Komplement ist, daß einmal die Doppeldeutigkeit der Null nicht auftritt, und zum zweiten, daß die Korrekturaddition bei der Subtraktion nicht mehr durchgeführt werden muß.

Im mathematischen Sinne existiert die Summe $A+B$ und das Produkt $A \cdot B$ zweier positiver ganzer Zahlen $A$ und $B$ immer. Wie sehen nun diese Summe und das Produkt in der Rechnerarithmetik aus? Solange das mathematische Ergebnis eine Zahl innerhalb der Zahlendarstellung des Rechners ergibt, sind natürlich beide, das mathematische Resulat und das Rechnerresultat, identisch gleich. Wenn nun aber das mathematische Ergebnis außerhalb des Zahlenbereiches des Rechners liegt, ergeben sich Unterschiede. Im allgemeinen gehen die bits, die eine höhere Wertigkeit als die höchstwertige Stelle des Rechners besitzen, einfach verloren. Manche Rechner geben in diesem Fall eine Fehlermeldung aus. Wir studieren diese sogenannte Überlauf- Arithmetik für den einfachen Fall eines Modellrechners mit 4 bit Zahlendarstellung. Wir haben dann die folgende Zahlendarstellung.

Tabelle 3:

Dualzahl	Dezimalzahl	Dezimalzahl
	(1-er Kompl.)	(2-er Kompl.)
0111	7	7
0110	6	6
0101	5	5
0100	4	4
0011	3	3
0010	2	2
0001	1	1
0000	+0	0
1111	-0	-1
1110	-1	-2
1101	-2	-3
1100	-3	-4
1011	-4	-5
1010	-5	-6
1001	-6	-7
1000	-7	-8

Bilden wir z.B. die Summe der Dezimalzahlen 5 und 6, so erhalten wir bei der Addition der entsprechenden Dualzahlen die Summe 1011. Dieses entspricht aber laut obiger Tabelle der Dezimalzahl -4 bei der 1-er Komplement Dartstellung und -5 bei der 2-er Komplement Darstellung. Entsprechend ergibt das Produkt aus 5 und 6 die Dualzahl 11110. Die höchste Stelle geht verloren, da, wie wir oben angenommen haben, unser Rechner nur 4 bits hat. Es verbleibt also die Zahl 1110. Dieses entspricht der Dezimalzahl -1 oder -2 im 1-er oder 2-er Komplement. Bilden wir dagegen das Produkt der Dezimalzahlen 5 und 7, so gibt der Rechner das Resultat 0011 aus, was gleichbedeutend mit der Dezimalzahl 3 ist. Für unsere weiteren Diskussionen müssen wir zunächst eine Größe definieren, die uns im folgenden häufig begegnen wird:
Satz: Sind $a$ und $b$ zwei ganze Zahlen und ist $b \neq 0$, so gibt es stets zwei andere Zahlen $q$ und $r$, so daß die Gleichung

$$a = b q + r$$ (3)

gilt. Dabei kann die Zahl $r$ stets der zusätzlichen Bedingung unterworfen werden, daß

$$0 \leq r < \vert b\vert$$ (4)

sein soll. Durch diese doppelte Forderung sind $q$ und $r$ eindeutig bestimmt. Man nennt $r$ den kleinsten nicht negativen Rest von $a$ bei der Teilung durch $b$ oder auch den kleinsten nicht negativen Rest ,,modulo b''. Man schreibt dafür auch

$$r = mod(a,b)$$ (5)

Diese Modulo- Funktion ist in jeder Computersprache bereits als Systemroutine enthalten.

Seien nun $A$ und $B$ zwei ganze positive Zahlen (wir beschränken im folgenden auf positive Zahlen). Sei ferner $C$ die Summe oder das Produkt von $A$ und $B$ im mathematischen Sinne und $C_{R}$ die mit einem Rechner berechnete Summe oder das Produkt. Der Rechner habe eine n-bit Arithmetik. Dann gilt für $C_{R} \geq 0$ die Relation

$$mod(C,2^{n-1}) = C_{R}$$ (6)

und für $C_{R} < 0$ die Relation

$$mod(C,2^{n-1}) = C_{R} + (2^{n-1} - 1) \; \; f''ur \; 1-er \; Komplement$$ (7)

$$mod(C,2^{n-1}) = C_{R} + (2^{n-1} - 1) + 1 \; \; \; \; f''ur \; 2-er \; Komplement$$ (8)

Die Schreibweise auf der rechten Seite der Gleichung (8) ist wichtig. Statt $(2^{n-1}-1)+1$ hätte man auch einfach $2^{n-1}$ schreiben können. Diese Zahl gibt es aber nicht auf dem Rechner. Die Vorschrift auf der rechten Seite der Gleichung (8) lautet also im einzelnen: 1. berechne mit Hilfe der Rechnerarithmetik $C_{R}$; 2. addiere die größte auf dem Rechner darstellbare Zahl, nämlich $2^{n-1}-1$, hinzu; 3. addiere zum Ergebnis eine 1. Man nennt diese Regeln die Überlauf- Arithmetik positiver Zahlen. Diese Regeln kann man leicht an Hand von Beispielen überprüfen. Wir haben diese Überlauf-Arithmetik hier eingehender erläutert, da wir die Formal (8) in einem späteren Tutorial zur Konstruktion eines Hardware- Zufallszahlengenerators verwenden werden.

Gleitkomma- Darstellung
Viele Rechner unterscheiden bei der Zahlendarstellung zwischen Festkomma- und Gleitkomma- Darstellung. Die ganzen Zahlen werden, wie bereits oben erläutert, im Dualcode mit m=0 in Formel (1) dargestellt, während reelle Zahlen entweder in Festkomma- Darstellung mit $m \neq 0$ oder in der Gleitkomma- Form

$$w= \pm x \cdot 10^{m}$$ (9)

dargestellt werden. Gespeichert wird in dieser Darstellung das Vorzeichen in einem bit (Vorzeichenbit), der Exponent $m$ und die Mantisse $x$ in jeweils getrennten bit- Feldern. Hierbei ist die Mantisse $m$ je nach Rechner eine Zahl zwischen 0 und 1 oder zwischen 1 und 2. Diese Darstellungsart hat den Vorteil, daß man sehr große und sehr kleine Zahlen darstellen kann. Die Genauigkeit der Mantisse, und damit die Anzahl der signifikanten Stellen in der Zahlendarstellung, ist aber ebenfalls beschränkt. Jeder Rechner hat eine ihm eigene Form der Mantissen- Darstellung. Wir werden im folgenden nur Zufallszahlen- Algorithmen beschreiben, die auf der Zahlendarstellung von ganzen Zahlen beruhen. Daher gehen wir nicht weiter auf die Gleitkomma- Darstellung ein.

Dezimalcodes
Moderne Rechner verwenden Dezimalcodes für die Ein- und Ausgabe von Daten, schon deshalb, weil der Mensch an das Dezimalzahlensystem gewöhnt ist, und der Computer für den Menschen da ist und nicht umgekehrt. Ein Dezimalzahlencode, bei dem jeder Stelle einer Zahl zehn verschiedene elektrische Zustände zugeordnet sind, ist für die technische Realisierung durch digitale Schaltungen ungeeignet. Wir werden uns daher mit der binären Darstellung von Dezimalzahlen befassen müssen, und hierbei insbesondere mit den BCD- Codes (englisch: binary coded decimal code). Diese Codes sind dadurch gekennzeichnet, daß jede einzelne Dezimalziffer unabhängig von der anderen codiert ist. Im dualen BCD- Code ergibt sich damit für die Ziffer 184 die Codierung

0001	1000	0100
1	8	4

Damit jede der 10 Dezimalstellen von 0 bis 9 binär codiert werden kann, sind mindestens 4 bit erforderlich. Aus diesem Grund spricht man auch von 4-bit Codes oder tetradischen Codes. Die 4 bits nennt man auch 1 byte (die Bedeutung von einem byte ist allerdings nicht eindeutig, in manchen Anwendungen werden auch 6 bzw. 8 bits als ein byte bezeichnet). Da man mit 4 bits 16 Zeichen darstellen kann, verbleiben 6 nicht benötigte Codewörter, die als Pseudodezimalzahlen oder Pseudotetraden bezeichnet werden.

Es gibt eine enorm große Anzahl ( $\approx 2.9 \cdot 10^{10}$) von Möglichkeiten, 4 bit Codes zu konstruieren. In der Praxis werden hiervon jedoch nur wenige Möglichkeiten ausgenutzt. In der folgenden Tabelle wird gezeigt, wie sich einige dieser Codes durch Einschieben von Pseudotetraden aus dem Dualcode entwickeln lassen.

Tabelle 4:

				Dualcode	BCD	Codes
$2^{3}$	$2^{2}$	$2^{1}$	$2^{0}$		8421	Aitken	3 Excess	5421	5311
0	0	0	0	0	0	0		0	0
0	0	0	1	1	1	1		1	1
0	0	1	0	2	2	2		2
0	0	1	1	3	3	3	0	3	2
0	1	0	0	4	4	4	1	4	3
0	1	0	1	5	5		2		4
0	1	1	0	6	6		3
0	1	1	1	7	7		4
1	0	0	0	8	8		5	5	5
1	0	0	1	9	9		6	6	6
1	0	1	0	10			7	7
1	0	1	1	11		5	8	8	7
1	1	0	0	12		6	9	9	8
1	1	0	1	13		7			9
1	1	1	0	14		8
1	1	1	1	15		9

Übungen

Aufgabe 1: Für einen 32-bit Rechner mit Zahlendarstellung im 2-er Komplement berechne man die folgenden dezimalen Ausdrücke:
a) 37956 * 69069;
b) 1729358476 + 2010004738;
c) 1729358476 - 2010004738.
Schreiben Sie die Ausdrücke a) bis c) und deren Lösungen auch im Hexadezimalsystem.

Aufgabe 2: Schreiben Sie Programm- Routinen für die doppelt genaue (64 bit) Addition, Subtraktion, Multiplikation und Division zweier 32-bit Zahlen in 2-er Komplement Darstellung.

Aufgabe 3: Im folgenden Applet finden Sie eine Schaltung für einen 2-bit Volladdierer. Erweitern Sie die Schaltung zu einem 3-bit Volladdierer.

Aufgabe 4: Entwerfen Sie mit Hilfe des Applets von Aufgabe 3 einen Schaltplan aus NAND- und NOT- Verknüpfungen für einen 1-bit Vollsubtrahierer.