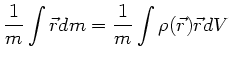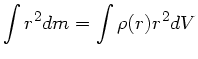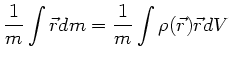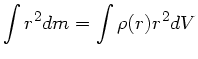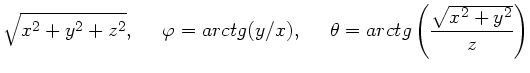Rechenübung am 18. November 1999
Berechnung von
Schwerpunkten und Trägheitsmomenten
Der Schwerpunkt und das Trägheitsmoment sind durch ähnliche
Integralausdrücke definiert:
Allerdings sind in diesen beiden Formeln das 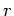 völlig anders
definiert. Beim Schwerpunkt ist
völlig anders
definiert. Beim Schwerpunkt ist 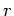 der Abstand von einem festen
Punkt, beim Trägheitsmoment ist
der Abstand von einem festen
Punkt, beim Trägheitsmoment ist 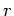 der Abstand von der Drehachse.
Einfache Beispiele wurden bereits in der Vorlesung diskutiert.
Zur Übung sollen hier weitere Beispiele gerechnet werden.
Um diese Integrale lösen zu können, benötigt man allerdings häufig
Zylinder- und Kugelkoordinaten. Diese erhält man aus den kartischen
Koordinaten durch die Umrechnung:
der Abstand von der Drehachse.
Einfache Beispiele wurden bereits in der Vorlesung diskutiert.
Zur Übung sollen hier weitere Beispiele gerechnet werden.
Um diese Integrale lösen zu können, benötigt man allerdings häufig
Zylinder- und Kugelkoordinaten. Diese erhält man aus den kartischen
Koordinaten durch die Umrechnung:
1. Zylinderkoordinaten:
2. Kugelkkordinaten:
Die Volumenelemente sind gegeben durch:
1. Zylinderkoordinaten:
Aufgabe 1:
Gegeben sei ein homogener gerader Kreiskegel der Masse 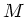 und Höhe
und Höhe 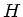 .
Die kreisförmige Basisfläche habe den Radius
.
Die kreisförmige Basisfläche habe den Radius 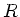 .
.
a) Ermitteln Sie den Schwerpunkt .
b) Wie groß ist das Trägheitsmoment bei Rotation um die
Symmetrieachse, die durch den Mittelpunkt des Basiskreises und durch die
Spitze des Kegels geht ?
Aufgabe 2:
Berechnen Sie das Trägheitsmoment einer Hohlkugel mit Radius 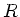 und
vernachlässigbar dünner Wandstärke.
und
vernachlässigbar dünner Wandstärke.
Harm Fesefeldt
2007-08-02