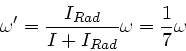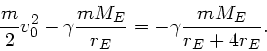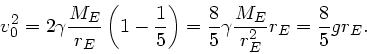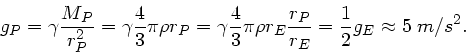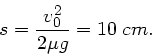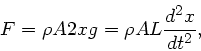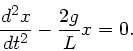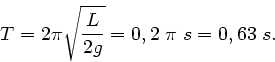Lösungen zur Übung Nr. 10 (Bonusübung)
Besprechung: Donnerstag, den 13. Januar 2000
Aufgabe 1: (Bonusaufgabe) (4 Punkte)
Mit der folgenden Abbildung gilt
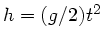 und
und
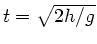 . Daraus folgt
. Daraus folgt
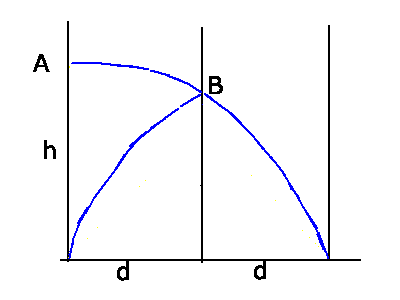
Aufgabe 2: (Bonusaufgabe) (4 Punkte)
Mit
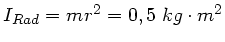 folgt der Drehimpuls
folgt der Drehimpuls
Die Drehimpulserhaltung verlangt
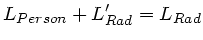 , d.h.
, d.h.
oder
b.z.w.
Aufgabe 3: (Bonusaufgabe) (4 Punkte)
Aus der Energieerhaltung folgt
Daraus folgt:
Also:
Aufgabe 4: (Bonusaufgabe) (4 Punkte)
Mit 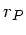 als Radius des Planeten und
als Radius des Planeten und 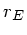 als Radius der Erde
gilt mit der Voraussetzung
als Radius der Erde
gilt mit der Voraussetzung
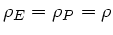 :
:
Aufgabe 5: (Bonusaufgabe) (4 Punkte)
Die kinetische Energie am Anfang der Bewegung muss gleich der gesamten
Reibungsenergie auf der Strecke 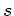 sein,
sein,
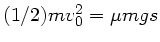 . Daher
. Daher
Aufgabe 6: (Bonusaufgabe) (4 Punkte)
Die rücktreibende Kraft ist gleich der Trägheitskraft,
wobei 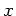 die Auslenkung aus der Ruhelage ist.
Daraus folgt die DGL
die Auslenkung aus der Ruhelage ist.
Daraus folgt die DGL
Vergleich mit
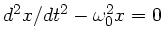 zeigt, dass
zeigt, dass
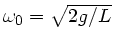 sein muss. Daraus folgt
sein muss. Daraus folgt
Harm Fesefeldt
2007-08-02
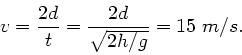
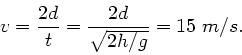

![]() folgt der Drehimpuls
folgt der Drehimpuls