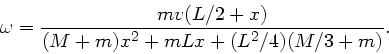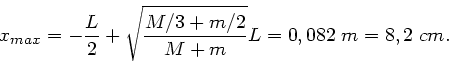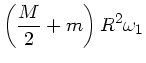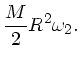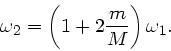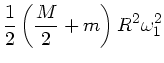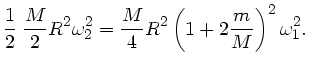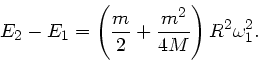Lösungen zur Übung Nr. 6
Besprechung: Donnerstag, den 2. Dezember 1999
Aufgabe 1: (7 Punkte)
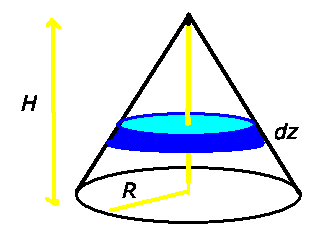
Wir zerlegen den Kreiskegel in Scheiben der Dicke 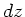 und Radius
und Radius
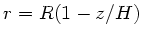 . Die Masse einer Kreisscheibe ist
. Die Masse einer Kreisscheibe ist
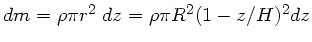 . Die Masse des gesamten Kreiskegels
ist dann
. Die Masse des gesamten Kreiskegels
ist dann
a) Aus Symmetriegründen liegen die 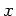 - und
- und 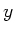 - Koordinaten des
Schwerpunktes bei
- Koordinaten des
Schwerpunktes bei 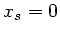 und
und 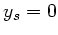 . Für die
. Für die 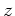 - Koordinate
folgt nach Definition:
- Koordinate
folgt nach Definition:
Ausgedrückt mit der Gesamtmasse folgt:
b) Das Trägheitsmoment einer Kreisscheibe ist nach Vorlesung
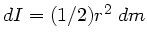 . Integration von
. Integration von 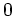 bis
bis 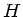 ergibt:
ergibt:
Aufgabe 2: (7 Punkte)
a) Der Drehimpuls vor dem Aufprall ist
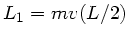 , der Drehimpuls
nach dem Aufprall
, der Drehimpuls
nach dem Aufprall
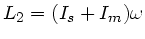 , mit den
Trägheitsmomenten
, mit den
Trägheitsmomenten
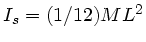 der Stange und
der Stange und
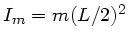 des
Geschosses. Drehimpulserhaltung ergibt:
des
Geschosses. Drehimpulserhaltung ergibt:
Aufgelöst nach 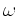 folgt:
folgt:
b) Falls die Achse nicht durch den Mittelpunkt verläuft, gilt nach dem
Steinerschen Satz für den Drehimpuls nach dem Stoß:
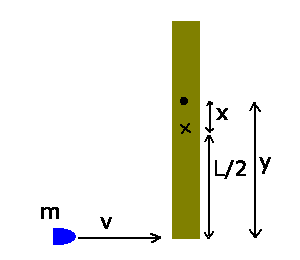
Gleichsetzen der Drehimpulse vor und nach dem Stoß führt jetzt auf:
Die Extremalbedingung
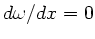 ergibt nach einiger Rechnung
(hoffentlich):
ergibt nach einiger Rechnung
(hoffentlich):
Der Punkt liegt also nur wenig vom Schwerpunkt der Stange entfernt.
Die Winkelgeschwindigkeit wird für diese Drehachse
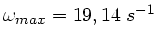 .
.
Aufgabe 3: (6 Punkte)
Der Drehimpuls 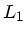 vorher und
vorher und 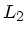 nachher ist gegeben durch
nachher ist gegeben durch
Drehimpulserhaltung verlangt 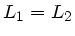 . Daraus folgt
. Daraus folgt
Die Winkelgeschwindigkeit vergrößert sich also.
b) Für die Energien gilt entsprechend:
Die Zunahme der Energie ist:
Diese Energie wird von der Person aufgebracht, indem sie gegen die
Zentrifugalkraft Arbeit leisten muss.
Aufgabe 4: (Bonusaufgabe) (10 Punkte)
Siehe z.B Demtröder Band I, Seite 125 - 128 oder Lehrbücher der
theoretischen Physik.
Harm Fesefeldt
2007-08-02
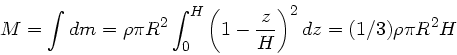
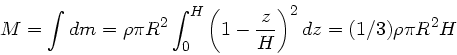

![]() - und
- und ![]() - Koordinaten des
Schwerpunktes bei
- Koordinaten des
Schwerpunktes bei ![]() und
und ![]() . Für die
. Für die ![]() - Koordinate
folgt nach Definition:
- Koordinate
folgt nach Definition:
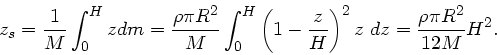
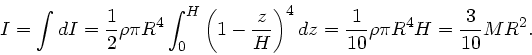
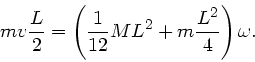
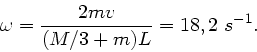
![\begin{displaymath}
L_{2} = \left( \frac{1}{12} M L^{2} + Mx^{2} \right) \omega ...
... \frac{L^{2}}{4} \left( \frac{M}{3} + m \right) \right] \omega
\end{displaymath}](img23.gif)