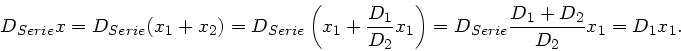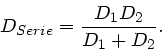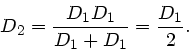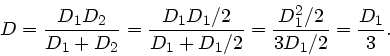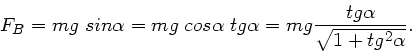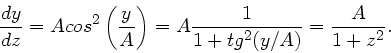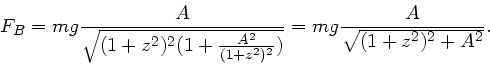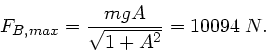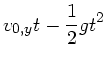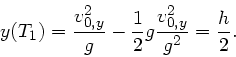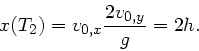Lösungen zur Übung Nr. 3
Besprechung: Donnerstag, den 11. November 1999
Aufgabe 1: (7 Punkte)
Wir diskutieren zunächst allgemein die Hintereinanderschaltung
und Parallelschaltung zweier beliebiger Federn mit Federkonstanten
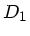 und
und 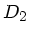 . Bei der Hintereinanderschaltung (Serienschaltung)
ist die Kraft in der gesamten Feder gleich, daher gilt
. Bei der Hintereinanderschaltung (Serienschaltung)
ist die Kraft in der gesamten Feder gleich, daher gilt
wobei die Gesamtauslenkung gleich der Summe der Einzelauslenkungen ist,
d.h.
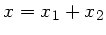 .
.
Diese Gleichungen können umgeformt werden zu
Daher muss also gelten
Bei der Parallelschaltung teilt sich die angreifende Kraft 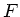 auf die
einzelnen Federn auf:
auf die
einzelnen Federn auf:
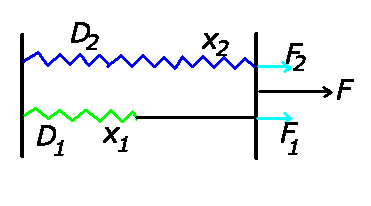
Daher gilt:
Mit
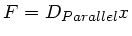 und
und
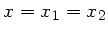 erhält man in diesem Fall
einfach
erhält man in diesem Fall
einfach
und
Diese Formeln erinnern uns stark an die Serien- und Parallelschaltung
von Widerständen in der Elektrizitätslehre.
Wenden wir im Folgenden diese Formeln auf unser Problem an.
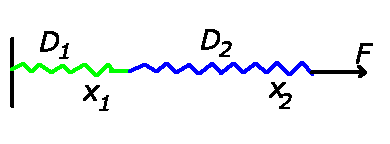
a) Wir teilen die Feder in drei gleiche Teile mit jeweils der Federkonstanten
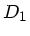 . Die zweite Feder besteht dann aus einer Serienschaltung von
zweien dieser Federn:
. Die zweite Feder besteht dann aus einer Serienschaltung von
zweien dieser Federn:
Die Serienschaltung von 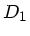 und
und 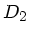 muss dann wieder die
ursprüngliche Feder ergeben:
muss dann wieder die
ursprüngliche Feder ergeben:
Die kürzere Feder hat also die Federkonstante 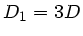 , die doppelt
so lange Feder die Konstante
, die doppelt
so lange Feder die Konstante
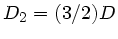 .
.
b) Für die Parallelschaltung beider folgt
Aufgabe 2: (8 Punkte)
a) Die beschleunigende Kraft ist immer längs der Bahn gerichtet. Mit den
Bezeichnungen der folgenden Skizze,
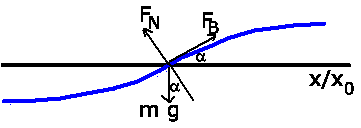
gilt:
In unserem Fall ist 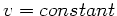 , daher
, daher 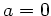 . Um
. Um 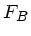 als Funktion
von
als Funktion
von 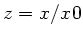 darzustellen, sind einige mathematische Tricks notwendig.
Zunächst ist
darzustellen, sind einige mathematische Tricks notwendig.
Zunächst ist
Der 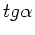 ist aber die Steigung der Bahnkurve. Aus
ist aber die Steigung der Bahnkurve. Aus 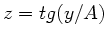 und
und
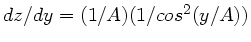 folgt
folgt
Wir setzen diesen Ausdruck in die Formel für 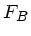 ein und erhalten
ein und erhalten
mit 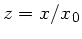 . Um die maximale Kraft zu bestimmen, könnte man
aus der Ableitung eine Extremalbedingung herleiten. Das ist in
diesem Fall allerdings nicht nötig. Man sieht sofort, daß
. Um die maximale Kraft zu bestimmen, könnte man
aus der Ableitung eine Extremalbedingung herleiten. Das ist in
diesem Fall allerdings nicht nötig. Man sieht sofort, daß 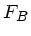 maximal wird, wenn der Nenner minimal wird, also für
maximal wird, wenn der Nenner minimal wird, also für 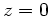 oder
oder
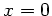 . Die Kraft in diesem Punkt ist
. Die Kraft in diesem Punkt ist
b) Auch die Arbeit könnte man umständlicherweise über ein
Integral bestimmen. Einfacher geht es aber, wenn wir uns an die
Vorlesung erinnern und die Hubarbeit bestimmen:
wobei 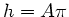 , da der
, da der 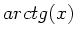 von
von 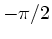 bis
bis 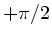 geht.
Also
geht.
Also
Aufgabe 3: (5 Punkte)
Die Geschwindigkeit des Körpers am Ende der schiefen Ebene ergibt
sich aus dem Energiesatz:
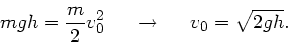 |
(1) |
Diese teilt sich auf in die Komponenten (wegen
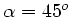 ):
):
Beim elastischen Aufprall bleibt der Impuls in 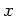 - Richtung unverändert,
während die
- Richtung unverändert,
während die 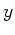 - Komponente das Vorzeichen ändert (entspricht dem
Stoß eines Körpers der kleinen Masse
- Komponente das Vorzeichen ändert (entspricht dem
Stoß eines Körpers der kleinen Masse 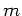 mit einem Körper unendlich
großer Masse). Daher erhalten wir nach dem Aufprall eine Wurfparabel
der Form (siehe Vorlesung Seite 27):
mit einem Körper unendlich
großer Masse). Daher erhalten wir nach dem Aufprall eine Wurfparabel
der Form (siehe Vorlesung Seite 27):
Das Maximum dieser Kurve erhalten wir aus
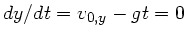 zum
Zeitpunkt
zum
Zeitpunkt
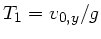 an der Höhe:
an der Höhe:
Die Weite folgt aus 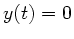 zum Zeitpunkt
zum Zeitpunkt
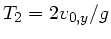 bei
der
bei
der 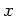 - Koordinate
- Koordinate
b) Beim inelastischen Stoß wird die 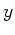 - Komponente des Impulses
absorbiert. Die Geschwindigkeit ist
- Komponente des Impulses
absorbiert. Die Geschwindigkeit ist
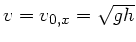 .
.
Harm Fesefeldt
2007-08-02