Lösungsvorschläge zur Übung Nr. 1
Besprechung: Donnerstag, den 28. Oktober 1999
Aufgabe 1: (6 Punkte)
Diese Aufgabe aus dem Bereich der Experimentalmathematik hat natürlich
nicht immer eine eindeutige Lösung. Die einfachsten Lösungen sind die
folgenden:
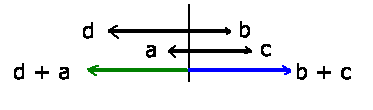
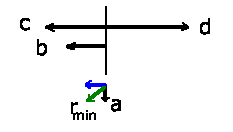
a) Den größten Vektor erhält man natürlich, wenn alle 4 Vektoren
gleichgerichtet sind, dann ist
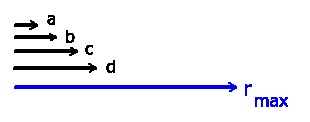
b) Der betragsmässig kleinste Vektor hat die Länge Null. Im
einfachsten Fall sind 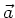 und
und 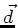 parallel und entsprechend
parallel und entsprechend
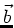 und
und 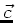 parallel, mit
parallel, mit
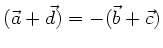 . Dann ist
. Dann ist
c) Hier erhalten wir den größten Vektor, wenn 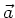 mit
mit
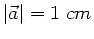 senkrecht
zur Ebene steht und alle anderen parallel zueinander in der Ebene liegen,
senkrecht
zur Ebene steht und alle anderen parallel zueinander in der Ebene liegen,
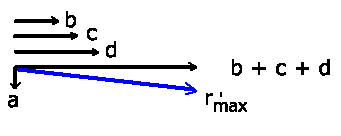
Dann ist
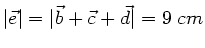 und
und
Den kleinsten Vektor erhalten wir jetzt, wenn wiederum 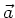 senkrecht
zur Ebene steht und der Vektor
senkrecht
zur Ebene steht und der Vektor
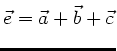 betragsmässig möglichst klein wird,
betragsmässig möglichst klein wird,
Aufgabe 3: (4 Punkte)
In der folgenden Skizze ist 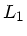 die Strecke des Schiffes bis zur Umkehr,
die Strecke des Schiffes bis zur Umkehr,
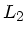 die Strecke des Schiffes bis zur Bergung der Kiste.
die Strecke des Schiffes bis zur Bergung der Kiste.
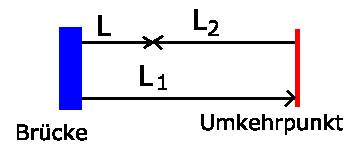
Damit ist
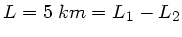 . Wenn
. Wenn 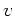 die Geschwindigkeit des
Stromes ist und
die Geschwindigkeit des
Stromes ist und 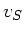 die Geschwindigkeit des Schiffes, so gilt
die Geschwindigkeit des Schiffes, so gilt
mit 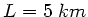 ,
,
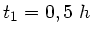 und
und
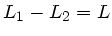 .
Aus den ersten beiden Gleichungen folgt:
.
Aus den ersten beiden Gleichungen folgt:
Dieser Ausdruck ist nur dann mit der dritten Gleichung des obigen
Systems verträglich, wenn
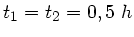 ist. Daher gilt:
ist. Daher gilt:
Aufgabe 4: (4 Punkte)
Das eine Flugzeug braucht 2 Stunden, um 1200 km zu fliegen. In dieser
Zeit hat das andere Flugzeug 1600 km zurückgelegt. Die Entfernung
beider beträgt
Aufgabe 2: (6 Punkte)
Die Dimensionen müssen auf beiden Seiten der Gleichungen übereinstimmen.
Dieses ergibt:
a)
Daraus folgt 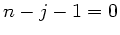 und
und 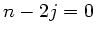 , also
, also 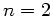 und
und 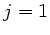 .
.
b)
Dieses ergibt 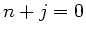 und
und 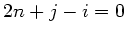 , was durch
, was durch 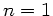 ,
, 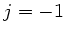 und
und
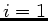 gelöst wird.
gelöst wird.
c) Das Argument der Sinusfunktion muss dimensionslos sein. Dieses ergibt
zunächst:
Also 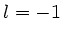 und
und 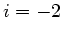 . Weiterhin muss der Faktor vor der Sinusfunktion
die Dimension einer Länge haben.
. Weiterhin muss der Faktor vor der Sinusfunktion
die Dimension einer Länge haben.
Daher 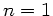 und
und 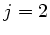 .
.
Harm Fesefeldt
2007-08-02
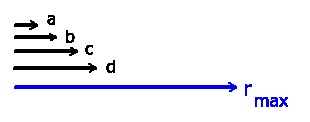
![]() und
und ![]() parallel und entsprechend
parallel und entsprechend
![]() und
und ![]() parallel, mit
parallel, mit
![]() . Dann ist
. Dann ist

![]() mit
mit
![]() senkrecht
zur Ebene steht und alle anderen parallel zueinander in der Ebene liegen,
senkrecht
zur Ebene steht und alle anderen parallel zueinander in der Ebene liegen,
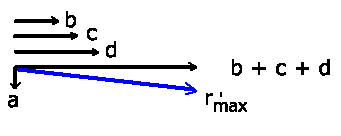
![]() und
und
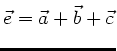 betragsmässig möglichst klein wird,
betragsmässig möglichst klein wird, 

![]() . Wenn
. Wenn ![]() die Geschwindigkeit des
Stromes ist und
die Geschwindigkeit des
Stromes ist und ![]() die Geschwindigkeit des Schiffes, so gilt
die Geschwindigkeit des Schiffes, so gilt
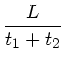
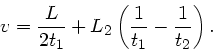
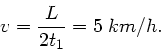
![$\displaystyle \left[ \frac{m}{s} \right]^{n}$](img32.gif)
![$\displaystyle k \left[ \frac{m}{s^{2}} \right]^{j} [m]$](img33.gif)
![$\displaystyle \left[ \frac{m^{n-j-1}}{s^{n-2j}} \right]$](img34.gif)
![\begin{displaymath}
1 = \left[ \frac{m}{s^{2}} \right]^{n} \left[ \frac{m}{s} \right]^{j}
[s]^{i} = \left[ \frac{m^{n+j}}{s^{2n+j-i}} \right].
\end{displaymath}](img40.gif)
![\begin{displaymath}
1 = [m] [s]^{i} \left[ \frac{m}{s^{2}} \right]^{l} =
\left[ \frac{m^{l+1}}{s^{2l-i}} \right].
\end{displaymath}](img46.gif)
![$\displaystyle \left[ \frac{m}{s^{2}} \right]^{n} [s]^{j}$](img50.gif)
![$\displaystyle \left[ \frac{m^{n-1}}{s^{2n - j}} \right]$](img51.gif)