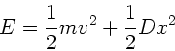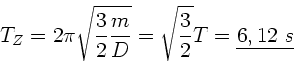Physik I, WS 1993/94
Rechenübungen am 20. Januar 1994
Aufgabe 1:
Ein Kupferwürfel der Kantenlänge 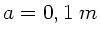 gleitet über eine
um
gleitet über eine
um 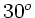 geneigte, geölte Fläche. Kupfer hat die Massendichte
geneigte, geölte Fläche. Kupfer hat die Massendichte
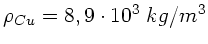 . Die Dicke der Ölschicht
beträgt
. Die Dicke der Ölschicht
beträgt
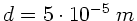 , die Zähigkeit des Öls ist
, die Zähigkeit des Öls ist
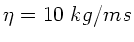 . Wie groß ist die stationäre Geschwindigkeit des
Würfels ?
. Wie groß ist die stationäre Geschwindigkeit des
Würfels ?
Aufgabe 2:
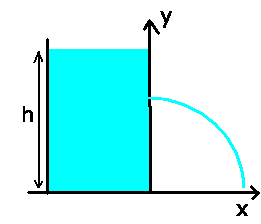
In einem Gefäß befindet sich Wasser mit einer Höhe 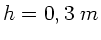 .
In welcher Höhe über dem Boden des Gefäßes muß man eine Öffnung
anbringen, damit das ausströmende Wasser möglichst weit entfernt
auf die Unterlage auftrifft, auf der das Gefäß steht ?
.
In welcher Höhe über dem Boden des Gefäßes muß man eine Öffnung
anbringen, damit das ausströmende Wasser möglichst weit entfernt
auf die Unterlage auftrifft, auf der das Gefäß steht ?
Aufgabe 3:
Eine Rakete fährt reibungsfrei auf einer Schiene und stößt kontinuierlich
(
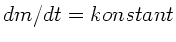 ) Treibgase mit der Geschwindigkeit
) Treibgase mit der Geschwindigkeit 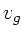 relativ
zur Rakete aus. Beim Start hat die Rakete die Masse
relativ
zur Rakete aus. Beim Start hat die Rakete die Masse
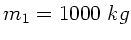 .
Wie groß ist die Masse der Rakete, wenn die Geschwindigkeit
der Rakete gleich der Geschwindigkeit
.
Wie groß ist die Masse der Rakete, wenn die Geschwindigkeit
der Rakete gleich der Geschwindigkeit 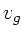 der Treibgase ist ?
der Treibgase ist ?
Aufgabe 4:
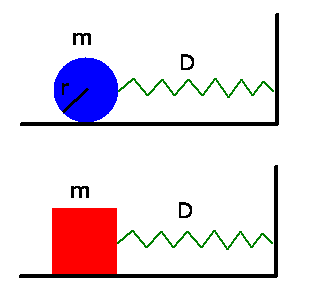
An der Achse eines Vollzylinders der Masse 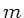 und Trägheitsmoment
und Trägheitsmoment
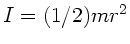 ist eine Feder der
Federkonstanten
ist eine Feder der
Federkonstanten 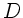 befestigt. Das andere Ende der Feder ist an einer
Wand arretiert. Der Zylinder rollt auf einer horizontalen Ebene, ohne zu
gleiten. Daneben gleitet ein Würfel der Masse
befestigt. Das andere Ende der Feder ist an einer
Wand arretiert. Der Zylinder rollt auf einer horizontalen Ebene, ohne zu
gleiten. Daneben gleitet ein Würfel der Masse 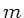 an einer Feder mit der
gleichen Federkonstanten
an einer Feder mit der
gleichen Federkonstanten 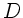 reibungsfrei auf der Ebene.
Wie groß ist die Schwingungsdauer des Zylinders, wenn die
Schwingungsdauer des Würfels
reibungsfrei auf der Ebene.
Wie groß ist die Schwingungsdauer des Zylinders, wenn die
Schwingungsdauer des Würfels 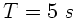 beträgt ?
beträgt ?
Lösungen
Aufgabe 1:
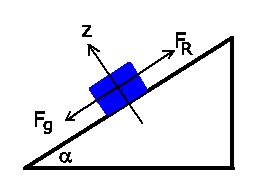
Es wirken zwei Kräfte, einmal die Schwerkraft
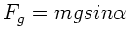 ,
zum anderen die Reibungskraft
,
zum anderen die Reibungskraft
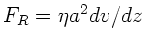 . Das
Geschwindigkeitsgefälle
. Das
Geschwindigkeitsgefälle 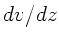 zwischen dem Würfel und der Ebene ist
linear, daher
zwischen dem Würfel und der Ebene ist
linear, daher 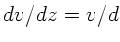 . Bei der stationären Bewegung heben sich
beide Kräfte gerade auf,
. Bei der stationären Bewegung heben sich
beide Kräfte gerade auf, 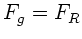 . Daraus folgt
. Daraus folgt
Aufgabe 2:
Für die Geschwindigkeit gilt
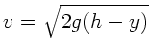 . Die Bewegung des
Wassers entspricht einem horizontalen Wurf, daher
. Die Bewegung des
Wassers entspricht einem horizontalen Wurf, daher
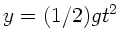 und
und
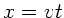 . Aus diesen drei Beziehungen folgt:
. Aus diesen drei Beziehungen folgt:
Die Extremalbedingung 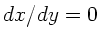 ergibt
ergibt
Aufgabe 3:
Für die Rakete gilt die Impulsbilanz:
Integration auf beiden Seiten liefert
In diesem Beispiel soll 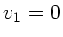 und
und
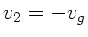 sein, daher
sein, daher
Aufgabe 4:
Die Gesamtenergie des Zylinders ist
Vergleichen wir diesen Ausdruck mit der Schwingungsdauer
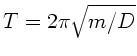 des Würfels ohne Rotation und der Energie
des Würfels ohne Rotation und der Energie
so folgt für die Schwingungsdauer des Zylinders
Harm Fesefeldt
2007-08-06



![]() ,
zum anderen die Reibungskraft
,
zum anderen die Reibungskraft
![]() . Das
Geschwindigkeitsgefälle
. Das
Geschwindigkeitsgefälle ![]() zwischen dem Würfel und der Ebene ist
linear, daher
zwischen dem Würfel und der Ebene ist
linear, daher ![]() . Bei der stationären Bewegung heben sich
beide Kräfte gerade auf,
. Bei der stationären Bewegung heben sich
beide Kräfte gerade auf, ![]() . Daraus folgt
. Daraus folgt
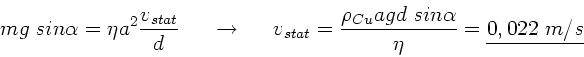
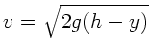 . Die Bewegung des
Wassers entspricht einem horizontalen Wurf, daher
. Die Bewegung des
Wassers entspricht einem horizontalen Wurf, daher
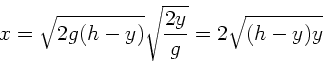
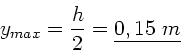

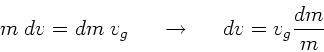
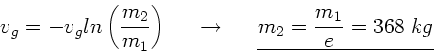
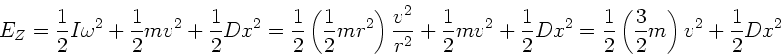
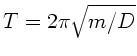 des Würfels ohne Rotation und der Energie
des Würfels ohne Rotation und der Energie