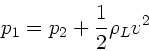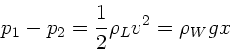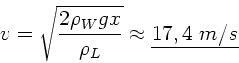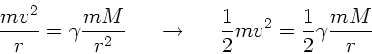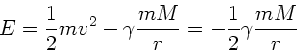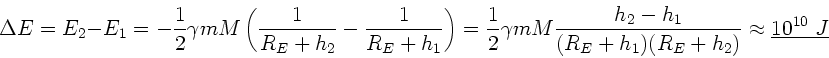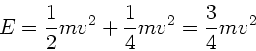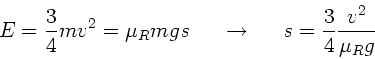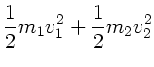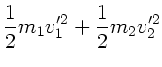Physik I, WS 1993/94
Lösungen zur Nachholklausur
Aufgabe 1: (8 Punkte)
Die Druckbilanz in den beiden Fällen ist
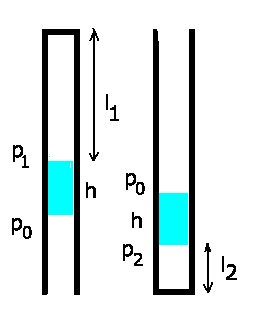
Nach Boyle-Mariotte ist
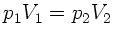 oder
oder
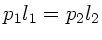 , da der der Querschnitt überall gleich ist.
Dann folgt
, da der der Querschnitt überall gleich ist.
Dann folgt
Aufgelöst nach 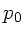 ergibt
ergibt
Aufgabe 2: (8 Punkte)
Die durch die Temperaturänderung hervorgerufene Kraft ist
Zusammen mit der Vorspannung 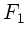 ergibt sich:
ergibt sich:
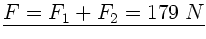
Aufgabe 3: (9 Punkte)
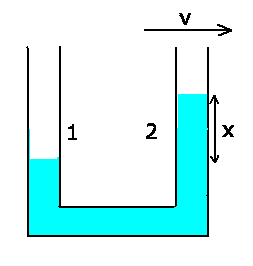
a) Es gilt die Bernoulli- Gleichung:
Der Term mit 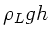 braucht hier nicht betrachtet zu werden,
da
braucht hier nicht betrachtet zu werden,
da 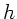 bei der Strömung konstant ist. Am Schenkel 1 ist
bei der Strömung konstant ist. Am Schenkel 1 ist 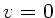 , daher
, daher
Die Druckdifferenz 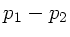 erzeugt die Flüssigkeitssäule
erzeugt die Flüssigkeitssäule
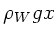 , daher
, daher
Aufgelöst nach 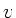 ergibt:
ergibt:
b) Die Flüssigkeit im Schenkel 2 steht natürlich höher.
Aufgabe 4: (9 Punkte)
Der Satellit hat eine stabile Kreisbahn, wenn zwischen der
Fliehkraft
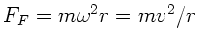 und der Gravitationskraft
und der Gravitationskraft
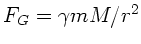 Gleichgewicht herrscht. Daher muß gelten:
Gleichgewicht herrscht. Daher muß gelten:
Die Gesamtenergie des Satelliten auf einer Kreisbahn mit Radius 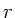 ist
also
ist
also
Die Energie 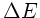 , die benötigt wird, um den Radius von
, die benötigt wird, um den Radius von
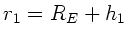 auf
auf
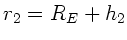 zu vergrößern, ist
dann
zu vergrößern, ist
dann
Aufgabe 5: (8 Punkte)
Die Energie des Rades ist zu Beginn der Bewegung
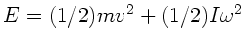 . Mit
. Mit 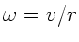 und
und
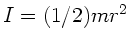 also
also
Diese Energie wird durch Rollreibung auf der Strecke 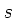 verbraucht:
verbraucht:
Zahlenwerte:
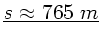
Aufgabe 6: (8 Punkte)
Hier gelten Impulssatz und Energiesatz:
Mit
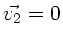 und
und 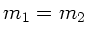 folgen die beiden Gleichungen
folgen die beiden Gleichungen
Quadrieren der ersten Gleichung ergibt
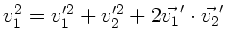 .
Zusammen mit der zweiten Gleichung folgt daraus:
.
Zusammen mit der zweiten Gleichung folgt daraus:
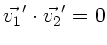 oder
oder
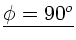 .
.
Harm Fesefeldt
2007-08-06

![]() oder
oder
![]() , da der der Querschnitt überall gleich ist.
Dann folgt
, da der der Querschnitt überall gleich ist.
Dann folgt
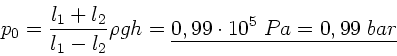
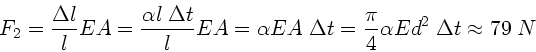
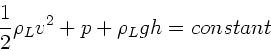

![]() braucht hier nicht betrachtet zu werden,
da
braucht hier nicht betrachtet zu werden,
da ![]() bei der Strömung konstant ist. Am Schenkel 1 ist
bei der Strömung konstant ist. Am Schenkel 1 ist ![]() , daher
, daher