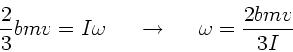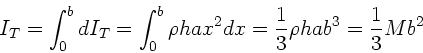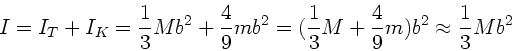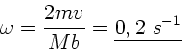Physik I, WS 1993/94
Lösungen zur Klausur
Besprechung: 3. Februar 1994
Aufgabe 1: (7 Punkte)
Anwendung des Hagen-Poiseuille'schen Gesetzes (siehe Skript Seite 160)
ergibt:
Der Druckunterschied 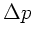 ist in beiden Schläuchen gleich, alle
anderen Konstanten natürlich ebenfalls. Die exakte Form des
Hagen- Poiseuille'schen Gesetzes ist in dieser Aufgabe nicht verlangt,
sondern lediglich die
ist in beiden Schläuchen gleich, alle
anderen Konstanten natürlich ebenfalls. Die exakte Form des
Hagen- Poiseuille'schen Gesetzes ist in dieser Aufgabe nicht verlangt,
sondern lediglich die 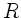 - und
- und 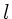 - Abhängigkeit. Nach
Aufgabenstellung ist
- Abhängigkeit. Nach
Aufgabenstellung ist 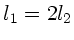 , daher
, daher
Für 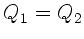 folgt also:
folgt also:
Aufgabe 2: (8 Punkte)
Die Gesamtenergie ist
wobei 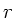 der Radius vom Mittelpunkt des Planeten ist. Anwendung der
Energieerhaltung ergibt:
der Radius vom Mittelpunkt des Planeten ist. Anwendung der
Energieerhaltung ergibt:
Auflösen nach 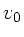 liefert:
liefert:
Mit
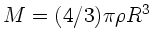 folgt
folgt
Aufgabe 3: (9 Punkte)
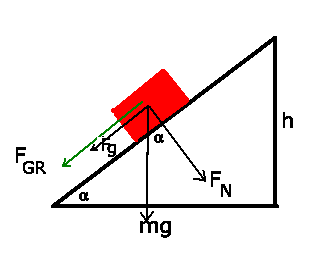
a) 1. Lösungsweg
Die Auflagekraft ist
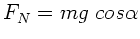 , die Gleitreibungskraft
daher
, die Gleitreibungskraft
daher
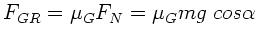 . Auf dem Weg
. Auf dem Weg
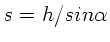 wird also die Arbeit
wird also die Arbeit
verbraten. Der Energiesatz lautet hiermit:
Aufgelöst nach 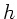 ergibt:
ergibt:
2. Lösungsweg
Der zweite Lösungsweg ist etwas komplizierter, wurde aber von unseren
Proberechnern gewählt.
Die Bewegungsgleichung des Klotzes auf der schiefen Ebene ist
Mit
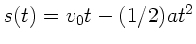 und
und
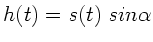 folgt:
folgt:
Die maximale Höhe wird erreicht, wenn 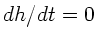 wird, daraus folgt
die hierzu notwendige Zeit
wird, daraus folgt
die hierzu notwendige Zeit
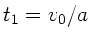 . Einsetzen in die vorherige
Formel liefert
. Einsetzen in die vorherige
Formel liefert
b) Das Verhältnis der rücktreibenden Schwerkraft
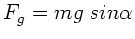 zur Haftreibungskraft
zur Haftreibungskraft
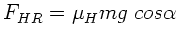 ,
,
ist größer als 1, daher gleitet der Klotz die Ebene wieder hinunter.
Aufgabe 4: (9 Punkte)
Die in der Seifenblase gespeicherte Energie ist
Diese Energie verteilt sich beim Zerplatzen auf die kinetische Energie
der entstehenden Tröpfchen:
Hierbei wurde ausgenutzt, daß nach Aufgabenstellung die Geschwindigkeiten
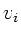 der einzelnen Tröpfchen gleich sind, also
der einzelnen Tröpfchen gleich sind, also 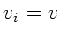 , und daß
die Gesamtmasse
, und daß
die Gesamtmasse 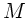 der Seifenblase gleich der Summe der Massen der
Tröpfchen sein muß. Daher folgt
der Seifenblase gleich der Summe der Massen der
Tröpfchen sein muß. Daher folgt
Aufgabe 5: (9 Punkte)
Die beiden Massen rotieren um ihren gemeinsamen Schwerpunkt. Dieser
liegt offensichtlich in der Mitte der Feder. Die Fliehkraft einer Masse ist
dann
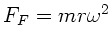 . Diese Kraft wird von der rücktreibenden
Federkraft
. Diese Kraft wird von der rücktreibenden
Federkraft
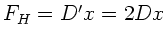 kompensiert, wobei die doppelte
Federkonstante zu nehmen, da die Feder halbiert wurde.
Mit
kompensiert, wobei die doppelte
Federkonstante zu nehmen, da die Feder halbiert wurde.
Mit 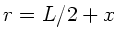 folgt also
folgt also
oder
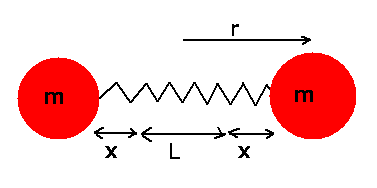
Die Energie der Rotation ist dann
Zahlenwerte:
Aufgabe 6: (8 Punkte)
Nach dem Drehimpulssatz muß der Drehimpuls
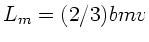 der Kugel
gleich dem Drehimpuls
der Kugel
gleich dem Drehimpuls
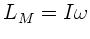 der Tür sein, wobei
der Tür sein, wobei 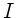 das
Trägheitsmoment ist:
das
Trägheitsmoment ist:
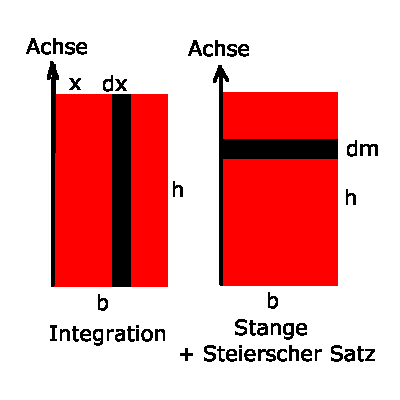
Das Trägheitsmoment kann auf zwei Wegen berechnet
werden, einmal durch direkte Integration, zum anderen mit Hilfe des
Trägheitsmomentes einer dünnen Stange und des Steinerschen Satzes.
Seien 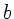 ,
, 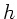 und
und 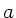 die Breite, Höhe und Dicke der Tür, so ist
für ein infinitesimales Volumen der Breite
die Breite, Höhe und Dicke der Tür, so ist
für ein infinitesimales Volumen der Breite 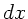 , Höhe
, Höhe 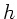 und Dicke
und Dicke 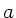 im Abstand
im Abstand 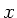 von der Aufhängung das infinitesimale Trägheitsmoment
von der Aufhängung das infinitesimale Trägheitsmoment
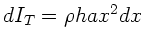 . Integration von
. Integration von 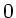 bis
bis 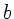 liefert
liefert
Dasselbe erhält man aus dem Steinerschen Satz. Das Trägheitsmomet einer
dünnen Stange der Länge 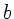 und Masse
und Masse 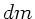 ist
ist
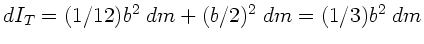 .
Summation über alle Stangen von der Höhe
.
Summation über alle Stangen von der Höhe 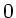 bis
bis 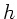 ergibt dann wiederum
ergibt dann wiederum
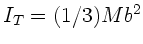 . Der Beitrag der kleinen Kugelmasse zum Trägheitsmoment
der Tür kann vernachlässigt werden.
. Der Beitrag der kleinen Kugelmasse zum Trägheitsmoment
der Tür kann vernachlässigt werden.
Einsetzen in die obige Gleichung ergibt
Harm Fesefeldt
2007-08-06
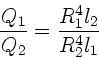
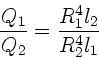
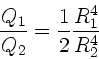
![\begin{displaymath}
\frac{d_{1}}{d_{2}} = \frac{R_{1}}{R_{2}} =
\underline{\sqrt[4]{2} = 1,19}
\end{displaymath}](img8.gif)
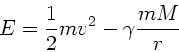
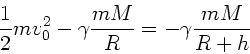
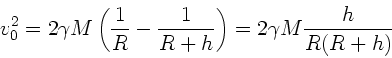
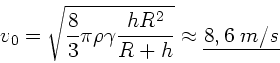

![]() , die Gleitreibungskraft
daher
, die Gleitreibungskraft
daher
![]() . Auf dem Weg
. Auf dem Weg
![]() wird also die Arbeit
wird also die Arbeit
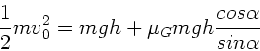
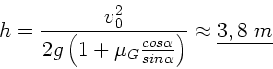
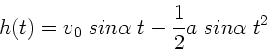
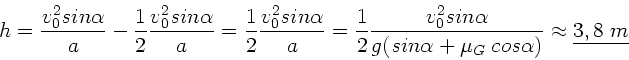
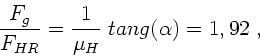
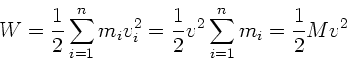
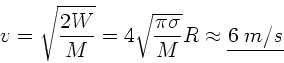
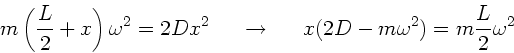
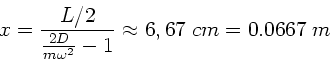
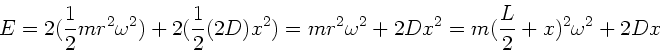

![]() der Kugel
gleich dem Drehimpuls
der Kugel
gleich dem Drehimpuls
![]() der Tür sein, wobei
der Tür sein, wobei ![]() das
Trägheitsmoment ist:
das
Trägheitsmoment ist: