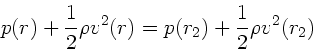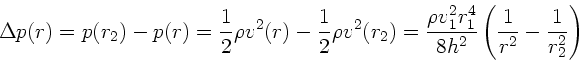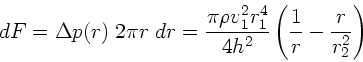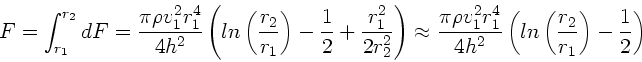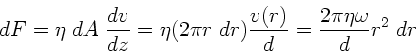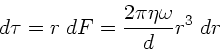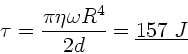Physik I, WS 1993/94
Lösungen zur Übung Nr. 12
Besprechung: 27. Januar 1994
Aufgabe 1: (5 Punkte)
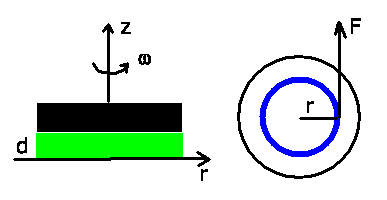
Die im folgenden gewählten Bezeichnungen sind in der Skizze angegeben:
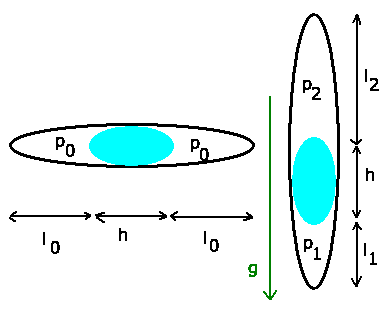
In vertikaler Lage gilt, wobei wir die Höhenabhängigkeit des Druckes
in den Luftsäulen vernachlässigen (
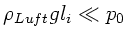 ),
),
Nach Boyle ist
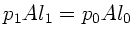 und
und
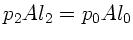 , wobei
, wobei 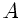 der Querschnitt des Röhrchens
ist. Daher
der Querschnitt des Röhrchens
ist. Daher
Aufgelöst nach 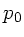 folgt:
folgt:
Aufgabe 2: (4 Punkte)
a) Nach Bernoulli gilt für die Drücke am Abfluß und an der Oberfläche
des Gefäßes:
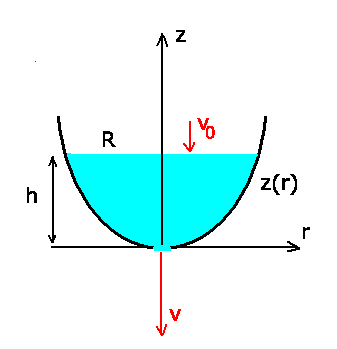
Hierbei ist 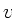 die Geschwindigkeit in der Öffnung und
die Geschwindigkeit in der Öffnung und 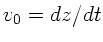 die Senkgeschwindigkeit des Wasserspiegels.
die Senkgeschwindigkeit des Wasserspiegels. 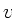 kann mit Hilfe der
Kontinuitätsgleichung,
kann mit Hilfe der
Kontinuitätsgleichung,
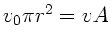 durch den aktuellen
Radius der Wasseroberfläche ausgedrückt werden. Daher folgt:
durch den aktuellen
Radius der Wasseroberfläche ausgedrückt werden. Daher folgt:
b) Damit die Uhr eine Stunde laufen kann, muß die Anfangshöhe des
Wasserspiegels 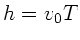 mit
mit
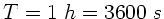 sein,
d.h.
sein,
d.h. 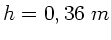 . Der maximale Radius ist daher
. Der maximale Radius ist daher
Aufgabe 3: (6 Punkte)
Die Geschwindigkeitsverteilung der Luft als Funktion des Radius 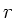 folgt
aus der Kontinuitätsgleichung
folgt
aus der Kontinuitätsgleichung
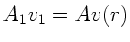 mit
mit
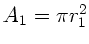 und
und 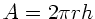 zu
zu
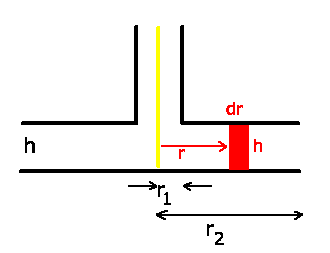
Die Anziehungskraft der Platten ist durch die Druckdifferenz des
statischen Außendrucks zum statischen Innendruck gegeben.
Sei 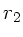 der Radius der Platten, so gilt nach Bernoulli für einen
beliebigen Radius
der Radius der Platten, so gilt nach Bernoulli für einen
beliebigen Radius 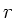 :
:
Der statische Druck 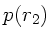 ist aber identisch mit dem statischen Aussendruck
(Randbedingung). Die Druckdifferenz ist also
ist aber identisch mit dem statischen Aussendruck
(Randbedingung). Die Druckdifferenz ist also
Die Kraft für ein infinitesimales Kreissegment mit Radius 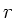 und Breite
und Breite
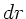 ist nun
ist nun
Die Gesamtkraft folgt durch Integration von 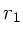 bis
bis 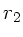 :
:
Im letzten Schritt wurde der Term mit
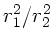 vernachlässigt.
Falls hier jemand von
vernachlässigt.
Falls hier jemand von 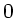 bis
bis 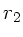 zu integrieren versucht, der bekommt
natürlich Schwierigkeiten mit dem
zu integrieren versucht, der bekommt
natürlich Schwierigkeiten mit dem 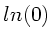 . Im übrigen darf man auch
den Beitrag für
. Im übrigen darf man auch
den Beitrag für 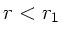 nicht berücksichtigen, da in diesem Bereich
natürlich keine Anziehungskraft zwischen den Platten herrscht.
nicht berücksichtigen, da in diesem Bereich
natürlich keine Anziehungskraft zwischen den Platten herrscht.
Zahlenwerte:
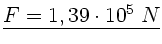 .
.
- Für diese Aufgabe sollten die wesentlichen 4 Schritte als
Anleitung in den Übungen am 20.1.94 erläutert werden:
- 1.
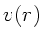 aus Kontinuitätsgleichung.
aus Kontinuitätsgleichung.
- 2.
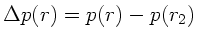 aus Bernoulli- Gleichung
aus Bernoulli- Gleichung
- 3.
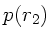 identisch mit dem Aussendruck
identisch mit dem Aussendruck
- 4.
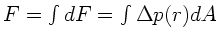 .
.
Aufgabe 4: (5 Punkte)
Die Bahngeschwindigkeit beim Radius 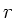 ist
ist
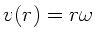 . Das
Geschwindigkeitsgefälle zwischen ruhender Platte und rotierender Scheibe
ist
. Das
Geschwindigkeitsgefälle zwischen ruhender Platte und rotierender Scheibe
ist 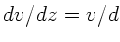 . Die aufzuwendende Kraft für einen inifinitesimalen
Kreisausschnitt ist also
. Die aufzuwendende Kraft für einen inifinitesimalen
Kreisausschnitt ist also
Entsprechend das aufzuwendende Drehmoment:
Integration von 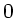 bis
bis 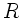 führt auf
führt auf
Für die Leistung ergibt sich
Harm Fesefeldt
2007-08-06


![]() ),
),
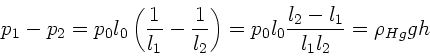
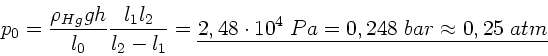
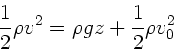

![]() die Geschwindigkeit in der Öffnung und
die Geschwindigkeit in der Öffnung und ![]() die Senkgeschwindigkeit des Wasserspiegels.
die Senkgeschwindigkeit des Wasserspiegels. ![]() kann mit Hilfe der
Kontinuitätsgleichung,
kann mit Hilfe der
Kontinuitätsgleichung,
![]() durch den aktuellen
Radius der Wasseroberfläche ausgedrückt werden. Daher folgt:
durch den aktuellen
Radius der Wasseroberfläche ausgedrückt werden. Daher folgt:
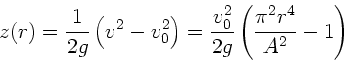
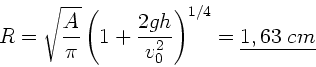
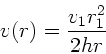

![]() der Radius der Platten, so gilt nach Bernoulli für einen
beliebigen Radius
der Radius der Platten, so gilt nach Bernoulli für einen
beliebigen Radius ![]() :
: