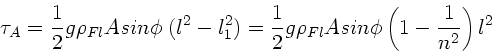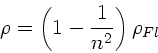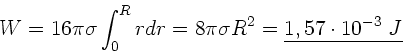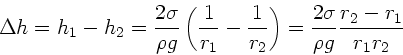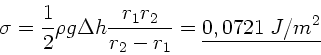Physik I, WS 1993/94
Lösungen zur Übung Nr. 11
Besprechung: 27. Januar 1994
Aufgabe 1: (6 Punkte)
Ohne die Trägheitskräfte der Abbremsung ergibt sich zunächst die Kraft
auf die Seitenwände folgendermaßen.
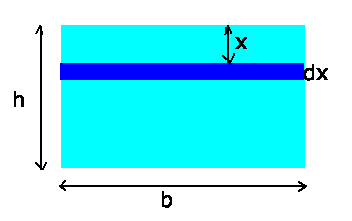
Der Druck in der Höhe 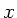 ist
ist 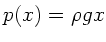 . Die Kraft auf ein
Flächenelement der Breite
. Die Kraft auf ein
Flächenelement der Breite 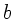 und Dicke
und Dicke 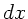 ist
ist
Intergration von 0 bis 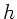 liefert:
liefert:
Diese Kraft ist für die Vorderseite und Rückseite identisch gleich.
Hinzu kommen während des Bremsvorganges die Trägheitskräfte. Die
Beschleunigung des Wagens ist
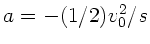 , die Trägheitskraft
also
, die Trägheitskraft
also
Insgesamt also:
wobei das Pluszeichen für die Vorderseite und das Minuszeichen für die
Rückseite gilt. Einsetzen der Zahlenwerte:
Aufgabe 2: (5 Punkte)
Sei 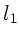 die Länge des Stabes ausserhalb des Wassers und
die Länge des Stabes ausserhalb des Wassers und 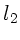 die
Länge im Wasser (
die
Länge im Wasser (
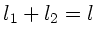 ). Nach Voraussetzung ist dann
). Nach Voraussetzung ist dann
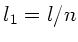 und
und
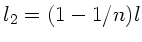 . Für ein Massenelement
. Für ein Massenelement 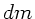 ist das Drehmoment der Schwerkraft (
ist das Drehmoment der Schwerkraft (
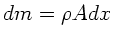 ):
):
Integration von 0 bis 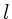 ergibt
ergibt
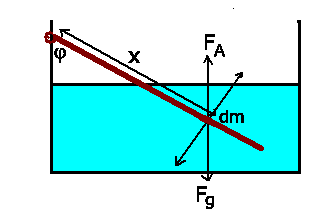
Das Drehmoment der Auftriebskraft ergibt sich entsprechend aus der
Integration von
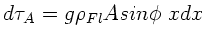 , diesmal aber
nur in den Grenzen von
, diesmal aber
nur in den Grenzen von  bis
bis  . Dieses ergibt
. Dieses ergibt
Im Gleichgewicht muß
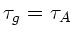 sein, daraus folgt:
sein, daraus folgt:
Aufgabe 3: (5 Punkte)
Die Oberflächenspannung war definiert als
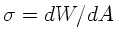 , wobei
, wobei 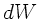 die
zur Vergrößerung
die
zur Vergrößerung 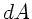 der Oberfläche notwendige Arbeit ist. Die gesamte
Oberfläche der Seifenblase ist
der Oberfläche notwendige Arbeit ist. Die gesamte
Oberfläche der Seifenblase ist
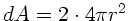 , wobei die doppelte
Kugeloberfläche zu nehmen ist. Mit
, wobei die doppelte
Kugeloberfläche zu nehmen ist. Mit
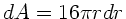 folgt für die Arbeit
folgt für die Arbeit
Integration in den Grenzen von 0 bis 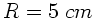 ergibt
ergibt
Aufgabe 4: (4 Punkte)
Da völlige Benetzung vorausgesetzt wurde, ist in der Formel auf Seite
145 des Skripts 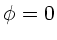 oder
oder 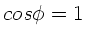 zu nehmen. Die Höhen in den
beiden Kapillaren sind dann
zu nehmen. Die Höhen in den
beiden Kapillaren sind dann
Daher folgt für die Höhendifferenz
Aufgelöst nach 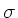 :
:
Harm Fesefeldt
2007-08-06


![]() ist
ist ![]() . Die Kraft auf ein
Flächenelement der Breite
. Die Kraft auf ein
Flächenelement der Breite ![]() und Dicke
und Dicke ![]() ist
ist
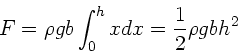
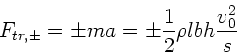
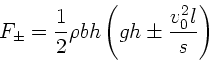
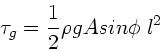

![]() , diesmal aber
nur in den Grenzen von
, diesmal aber
nur in den Grenzen von ![]() bis
bis ![]() . Dieses ergibt
. Dieses ergibt