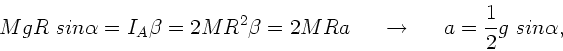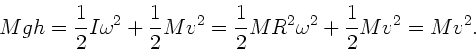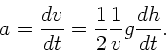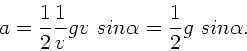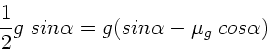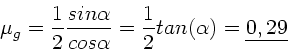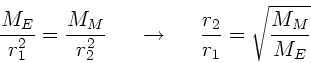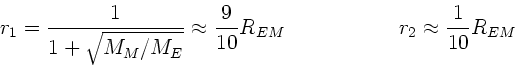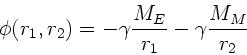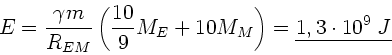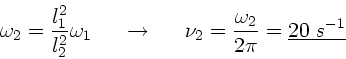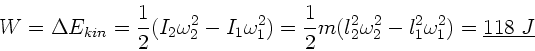Physik I, WS 1993/94
Lösungen zur Übung Nr. 10 (Bonusübung)
Besprechung: 20. Januar 1994
Aufgabe 1:
Das erste Rohr mißt die Summe von statischem Druck und Staudruck,
das zweite Rohr nur den Staudruck, da hier 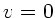 . Daher
. Daher
Die Druckdifferenz ist
woraus für die Geschwindigkeit folgt:
Pro Sekunde strömt das Flüssigkeitsvolumen
durch das Rohr.
Aufgabe 2: (4 Punkte)
Die Energie der Scheibe ist
wobei wir das Trägheitsmoment
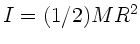 der Scheibe eingesetzt
haben. Die Winkelgeschwindigkeit ist
der Scheibe eingesetzt
haben. Die Winkelgeschwindigkeit ist
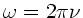 mit
mit
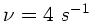 .
Da die Reibungskraft als konstant angenommen wurde, ist die
in Reibung umgesetzte Energie durch
.
Da die Reibungskraft als konstant angenommen wurde, ist die
in Reibung umgesetzte Energie durch
gegeben, wobei 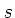 die gesamte Reibungsstrecke ist. Da die Abbremsung nach
10 Umdrehungen erfolgen soll, ist
die gesamte Reibungsstrecke ist. Da die Abbremsung nach
10 Umdrehungen erfolgen soll, ist
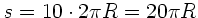 und damit
und damit
Auflösen nach F ergibt:
Aufgabe 3: (4 Punkte)
Das Hooksche Gesetz lautet
wobei 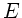 das Elastizitätsmodul und
das Elastizitätsmodul und 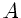 der Querschnitt des Drahtes
ist.
der Querschnitt des Drahtes
ist.
Die wirkende Kraft 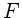 ist der Auslenkung proportional,
ist der Auslenkung proportional,
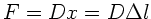 . Daher
. Daher
und
Aufgabe 4: (4 Punkte)
Nach dem Steinerschen Satz gilt für den Hohlzylinder
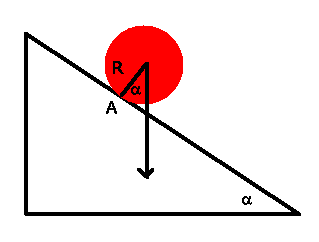
Die Beschleunigung 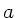 des Hohlzylinders kann auf zwei Wegen berechnet
werden, einmal über das Drehmoment
des Hohlzylinders kann auf zwei Wegen berechnet
werden, einmal über das Drehmoment
wobei wir die Winkelbeschleunigung hier mit
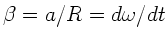 bezeichnet
haben, um eine Verwechselung mit dem Neigungswinkel
bezeichnet
haben, um eine Verwechselung mit dem Neigungswinkel 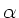 zu vermeiden.
Dasselbe Ergebnis folgt aus der Energieerhaltung:
zu vermeiden.
Dasselbe Ergebnis folgt aus der Energieerhaltung:
Mit
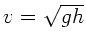 folgt
folgt
Mit
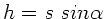 und
und
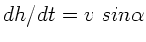 also ebenfalls
also ebenfalls
Für den Klotz gilt die Kräftegleichung
Da beide Beschleunigungen gleich sein sollten, muß gelten
oder, aufgelöst nach 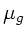 :
:
Aufgabe 5: (4 Punkte)
a) Es handelt sich natürlich um eine labile Gleichgewichtslage, da
bei einer kleinen Auslenkung der Körper nicht zur Gleichgewichtslage
zurückkommen würde, sondern eine Beschleunigung in Richtung Erde oder
Mond erfahren würde.
b) Seien 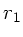 und
und 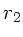 die Entfernungen von der Erde zum Körper
b.z.w. vom Mond zum Körper. Aus dem Kräftegleichgewicht folgt:
die Entfernungen von der Erde zum Körper
b.z.w. vom Mond zum Körper. Aus dem Kräftegleichgewicht folgt:
Da außerdem
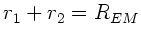 , folgt
, folgt
Das Gesamtpotential ist
Die Energiedifferenz zwischen Unendlich und dem Aufpunkt 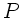 ist
ist
Da nach Definition der potentiellen Energie
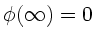 , folgt
, folgt
Aufgabe 6: (4 Punkte)
a) Zu Beginn ist die Winkelgeschwindigkeit
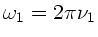 mit
mit
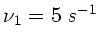 . Drehimpulserhaltung fordert, daß
. Drehimpulserhaltung fordert, daß
und daher
b) Die Arbeit ist durch die Differenz der kinetischen Energien gegeben:
Harm Fesefeldt
2007-08-06
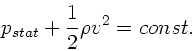
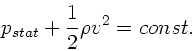
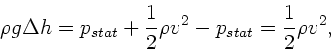
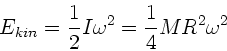
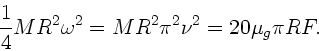
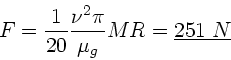
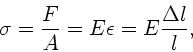
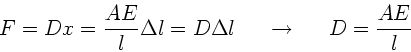
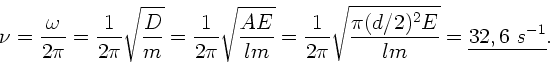

![]() des Hohlzylinders kann auf zwei Wegen berechnet
werden, einmal über das Drehmoment
des Hohlzylinders kann auf zwei Wegen berechnet
werden, einmal über das Drehmoment