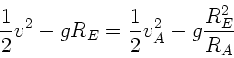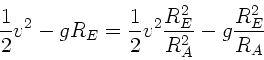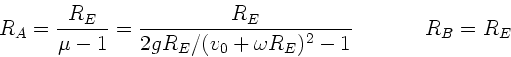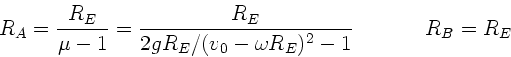Physik I, WS 1993/94
Lösungen zur Übung Nr. 9
Besprechung: 20. Januar 1994
Aufgabe 1: (4 Punkte)
Wir bezeichen Radius und Winkelgeschwindigkeit der Eigenrotation des
Planeten mit 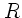 und
und 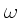 . Am Äquator herrscht die größte
Zentrifugalkraft. Damit nicht irgendeine Masse
. Am Äquator herrscht die größte
Zentrifugalkraft. Damit nicht irgendeine Masse 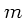 am Äquator nach außen
geschleudert wird, darf die Zentrifugalkraft nicht größer als die
Schwerkraft werden. Die maximale Winkelgeschwindigkeit der Eigenrotation
folgt dann aus
am Äquator nach außen
geschleudert wird, darf die Zentrifugalkraft nicht größer als die
Schwerkraft werden. Die maximale Winkelgeschwindigkeit der Eigenrotation
folgt dann aus
Die Masse des Planeten ist
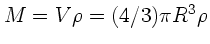 , daher
, daher
Wegen
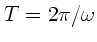 folgt
folgt
Das Zahlenbeispiel entspricht der mittleren Dichte der Erde. Bei dieser ist
die tatsächliche Periode
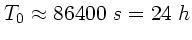 .
.
Aufgabe 2: (4 Punkte)
Die Formel (5) auf Seite 115 des Skripts lautet in den Schnittpunkten
der großen Halbachse mit der Ellipsenbahn ( in den Punkten
in den Punkten
 und
und 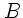 ):
):
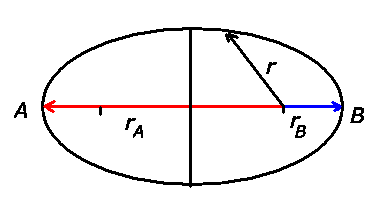
Der Drehimpuls 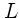 ist konstant, ist in den Punkten
ist konstant, ist in den Punkten 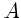 und
und 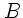 also
gleich. Da auch die Gesamtenergie während der Bewegung konstant ist,
gilt wegen
also
gleich. Da auch die Gesamtenergie während der Bewegung konstant ist,
gilt wegen
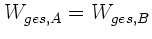 :
:
Einsetzen dieses Ausdrucks in die Formel für 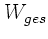 ergibt:
ergibt:
Aufgabe 3: (6 Punkte)
Aufgabe 4: (6 Punkte)
Die Bahnen beider Satelliten werden durch Ellipsenbahnen beschrieben.
Die Anfangsgeschwindigkeiten sind
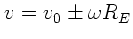 .
Wir rechnen zunächst nur für den Satelliten mit der größeren
Geschwindigkeit
.
Wir rechnen zunächst nur für den Satelliten mit der größeren
Geschwindigkeit
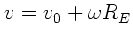 . Für den zweiten
Satelliten muß dann nur das Vorzeichen geändert werden.
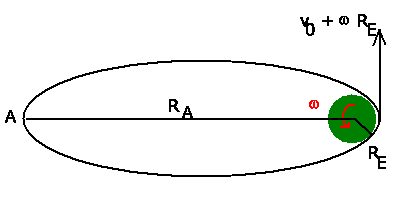
Den größten Abstand von der Erde erreicht der Satellit im
Schnittpunkt der Ellipsenbahn mit der großen Halbachse:
. Für den zweiten
Satelliten muß dann nur das Vorzeichen geändert werden.
Den größten Abstand von der Erde erreicht der Satellit im
Schnittpunkt der Ellipsenbahn mit der großen Halbachse:
Die Geschwindigkeit im Punkt 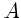 werde mit
werde mit 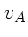 bezeichnet, dann
gilt wegen Drehimpulserhaltung:
bezeichnet, dann
gilt wegen Drehimpulserhaltung:
Erhaltung der Gesamtenergie verlangt, daß
mit
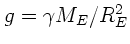 . Wir übernehmen
. Wir übernehmen 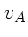 aus der
Drehimpuls- Formel und erhalten
aus der
Drehimpuls- Formel und erhalten
Mit der Abkürzung
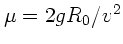 folgen die beiden Lösungen für
für
folgen die beiden Lösungen für
für 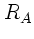 :
:
Die zweite Lösung ist trivial und entspricht dem Abschußort.
Für den anderen Satelliten gilt entsprechend:
Die maximalen Abstände der Satelliten vom Erdmittelpunkt sind somit
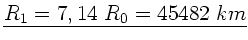 und entsprechend
und entsprechend
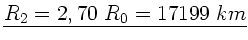 . Man sieht, daß die
Eigenrotation der Erde einen großen Einfluß auf die Ellipsenbahn hat.
. Man sieht, daß die
Eigenrotation der Erde einen großen Einfluß auf die Ellipsenbahn hat.
b) Der kritische Satellit ist der mit der größeren Geschwindigkeit
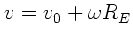 . Der maximale Abstand vom Erdmittelpunkt
wird Unendlich für
. Der maximale Abstand vom Erdmittelpunkt
wird Unendlich für 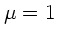 , d.h.
, d.h.
Der andere Satellit verschwindet dagegen erst bei
im Weltall. Die kritische Geschwindigkeit bei vertikalem Abschuß
beträgt
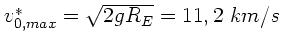 .
.
Harm Fesefeldt
2007-08-06
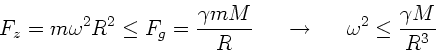
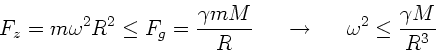
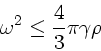
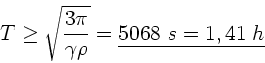

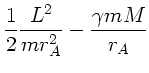
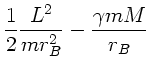
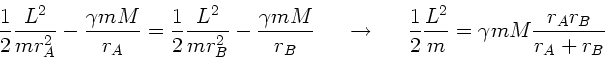
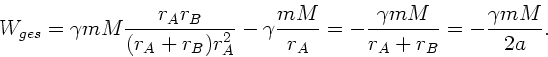

![]() werde mit
werde mit ![]() bezeichnet, dann
gilt wegen Drehimpulserhaltung:
bezeichnet, dann
gilt wegen Drehimpulserhaltung: