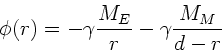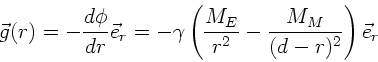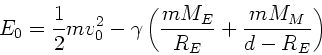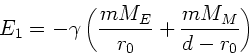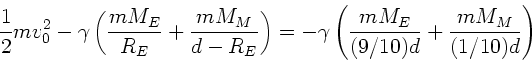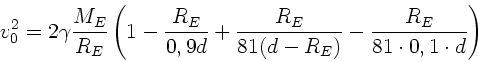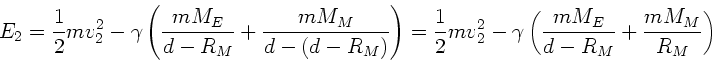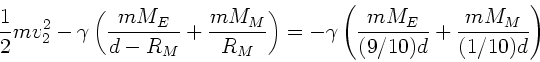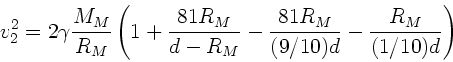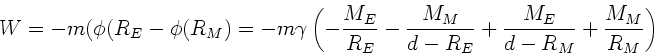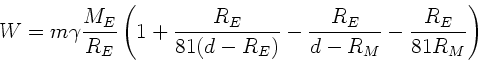Physik I, WS 1993/94
Lösungen zur Übung Nr. 8
Besprechung: 13. Januar 1994
Aufgabe 1: (5 Punkte)
Der Drehimpuls 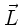 ist zeitlich konstant, während
ist zeitlich konstant, während 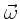 und die Figurenachse
und die Figurenachse 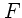 um
um 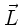 rotieren.
Wir verwenden allerdings ein Bezugssystem, in dem die
rotieren.
Wir verwenden allerdings ein Bezugssystem, in dem die 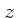 - Achse mit der
Figurenachse übereinstimmt. Dann rotieren
- Achse mit der
Figurenachse übereinstimmt. Dann rotieren 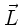 und
und 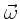 gleichermaßen um
gleichermaßen um 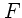 . Nach Vorlesung liegen beim kräftefreien Kreisel
. Nach Vorlesung liegen beim kräftefreien Kreisel
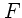 ,
, 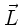 und
und 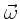 immer in einer Ebene.
immer in einer Ebene.
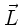 .
.
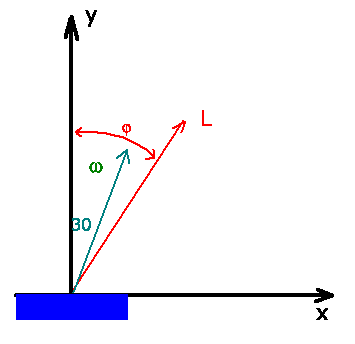
Komponentenzerlegung von 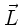 liefert für einen Zeitpunkt, in dem
liefert für einen Zeitpunkt, in dem
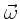 und
und 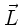 in der
in der 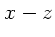 - Ebene liegen:
- Ebene liegen:
Nach Vorlesung ist
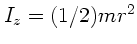 und nach Aufgabe 4c, Übung Nr.6,
gilt
und nach Aufgabe 4c, Übung Nr.6,
gilt
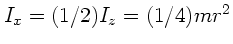 . Daher folgt:
. Daher folgt:
Manche werden wahrscheinlich
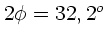 als Öffnungswinkel
des Kegels angeben.
als Öffnungswinkel
des Kegels angeben.
Aufgabe 2: (4 Punkte)
Die Cavendish- Torsionswaage wurde sehr ausführlich in der Vorlesung
behandelt und wird oft im Vordipom gefragt. Daher dient diese Aufgabe
dazu, daß jeder diesen Versuch noch einmal wiederholt.
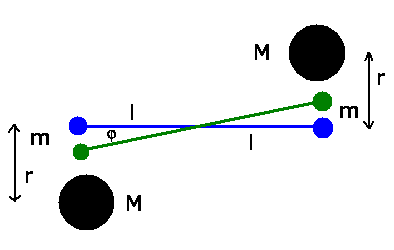
Aus der Periode der Pendelschwingungen ohne die großen Massen folgt die
Richtgröße des Torsionspendels:
Das Drehmoment
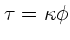 ist beim Maximalausschlag gerade dem
von der Schwerkraft
ist beim Maximalausschlag gerade dem
von der Schwerkraft 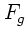 zwischen den kleinen und großen Massen
erzeugten Drehmoment gleich:
zwischen den kleinen und großen Massen
erzeugten Drehmoment gleich:
Daraus folgt für den Maximalausschlag
Einsetzen der Zahlenwerte:
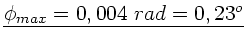 .
.
Aufgabe 3: (5 Punkte)
Wir wählen einen Kreisring der Dicke 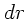 und Radius
und Radius 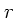 .
.
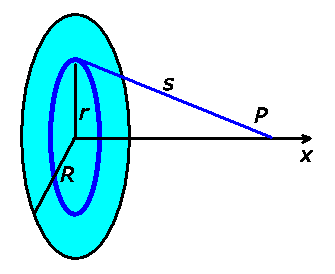
Dieser hat die Masse
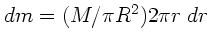 und erzeugt am Punkt
und erzeugt am Punkt
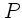 den Beitrag
den Beitrag
zum Potential. Integration über die gesamte Platte ergibt:
Für die Feldstärke gilt nach Vorlesung:
wobei wir den Einheitsvektor in 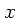 - Richtung eingeführt haben.
Daher:
- Richtung eingeführt haben.
Daher:
Das Minuszeichen zeigt an, daß die Feldstärke zur Platte hin gerichtet
ist.
Aufgabe 4: (6 Punkte)
Das Gravitationspotential des Gesamtsystems Erde- Mond ist die Summe
der Einzelpotentiale:
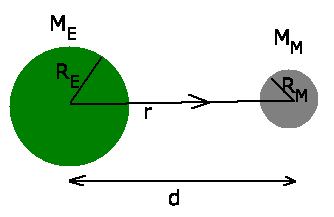
Zwischen Erdoberfläche und Mondoberfläche (
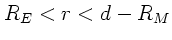 ) gilt
daher, wenn
) gilt
daher, wenn 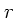 als Abstand vom Erdmittelpunkt definiert wird:
als Abstand vom Erdmittelpunkt definiert wird:
a) Die Feldstärke ist
und wird Null für
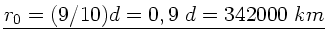 .
.
b) Wir verwenden den Energiesatz. Beim Abschuß der Rakete ist die
Gesamtenergie:
Wir erhalten die Mindestgeschwindigkeit beim Abschuß, wenn die
Geschwindigkeit bei der Strecke 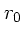 von Teil a) gerade Null wird.
An diesem Punkt ist somit die Energie
von Teil a) gerade Null wird.
An diesem Punkt ist somit die Energie
Wegen Energieerhaltung muß 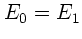 sein, daher
sein, daher
Auflösen nach 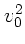 und Einsetzen der im Aufgabentext angegebenen
Beziehungen liefert:
und Einsetzen der im Aufgabentext angegebenen
Beziehungen liefert:
Zahlenwerte:
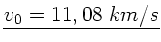 .
.
c) Die gleiche Übung nochmal. Die Energie beim Auftreffen auf dem Mond
ist
Da jetzt wegen Energieerhaltung 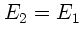 sein muß, gilt:
sein muß, gilt:
Auflösen nach 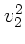 und Ersetzung der Erdmasse durch die Mondmasse
ergibt:
und Ersetzung der Erdmasse durch die Mondmasse
ergibt:
Zahlenwerte:
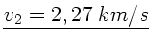 .
.
c) Die aufzuwendende Arbeit ist
oder
Zahlenwerte:
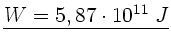 .
.
Harm Fesefeldt
2007-08-06


![]() liefert für einen Zeitpunkt, in dem
liefert für einen Zeitpunkt, in dem
![]() und
und ![]() in der
in der ![]() - Ebene liegen:
- Ebene liegen:
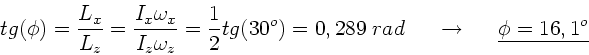

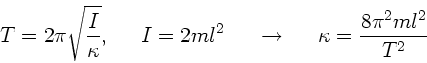
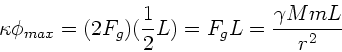
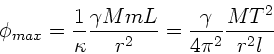

![]() und erzeugt am Punkt
und erzeugt am Punkt
![]() den Beitrag
den Beitrag
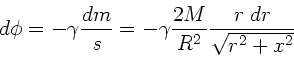
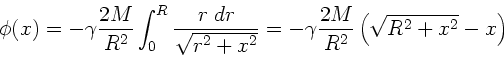
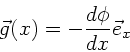
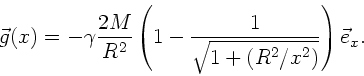

![]() ) gilt
daher, wenn
) gilt
daher, wenn ![]() als Abstand vom Erdmittelpunkt definiert wird:
als Abstand vom Erdmittelpunkt definiert wird: