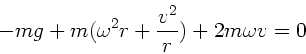Physik I, WS 1993/94
Lösungen zur Übung Nr. 7
Abgabetermin: 9. Dezember 1993
Aufgabe 1: (7 Punkte)
a) Die potentielle Energie ist für alle Zylinder am Anfang gleich. Sie wird vollständig in
kinetische Energie umgewandelt:
b) Man hat
sowie zusätzlich die Rollbedingung
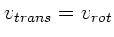 . Somit gilt für die Energien:
. Somit gilt für die Energien:
Es gilt also für alle Zylinder
 .
c) Alle Zylinder haben immer die gleiche kinetische Energie, also haben sie auch immer die gleiche
Translationsenergie. Da alle die gleiche Masse haben, ist auch die Geschwindigkeit immer gleich.
.
c) Alle Zylinder haben immer die gleiche kinetische Energie, also haben sie auch immer die gleiche
Translationsenergie. Da alle die gleiche Masse haben, ist auch die Geschwindigkeit immer gleich.
d) Stabile Rotationsachsen sind die Achsen mit dem größten Trägheitsmoment. Bei Rotation um
die Symmetrieachse gilt
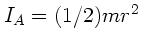 . Bei Rotation senkrecht zur Symmetrieachse
erhalten wir dagegen
. Bei Rotation senkrecht zur Symmetrieachse
erhalten wir dagegen
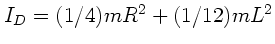 mit
mit
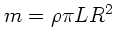 .
In der folgenden Tabelle sind die Werte für die verschiedene Radien dargestellt:
.
In der folgenden Tabelle sind die Werte für die verschiedene Radien dargestellt:
![$R[cm]$](img9.gif) |
![$L[cm]$](img10.gif) |
![$I_{A} \; [kg \cdot cm^{2}]$](img11.gif) |
![$I_{D} \; [kg \cdot cm^{2}]$](img12.gif) |
| 3 |
70,74 |
24,3 |
2264,02 |
| 10 |
6,37 |
270 |
153,26 |
| 20 |
1,59 |
1080 |
541,14 |
Der Zylinder mit dem kleinsten Radius wird also merkwürdigerweise anfangen zu torkeln. Die anderen beiden Zylinder
rollen stabil.
e) Aus
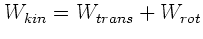 und
und
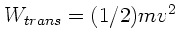 ,
,
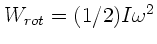 erhalten wir
erhalten wir
Wir müssen die Masse also so in den Zylinder einbauen, daß das Trägheitsmoment möglichst klein
wird. Das kann man durch einen Vollzylinder mit der Dichte
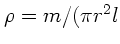 erreichen.
Am günstigsten ist es natürlich, die Masse in ein Kugellager einzubauen, sodaß nur noch die Kugeln
Rotationsenergie mitnehmen.
erreichen.
Am günstigsten ist es natürlich, die Masse in ein Kugellager einzubauen, sodaß nur noch die Kugeln
Rotationsenergie mitnehmen.
Aufgabe 2: (7 Punkte)
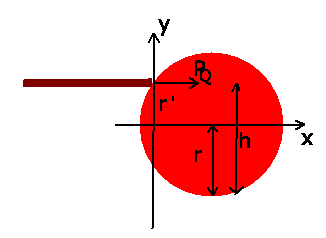
Die Dreimpulserhaltung verlangt, daß
Hieraus erhalten wir
Impulserhaltung ergibt zusätzlich
Zusammenm mit der Rollbedingung
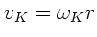 folgt:
folgt:
oder
Mit 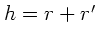 also:
also:
Aufgabe 3: (6 Punkte)
a) Bei einem ruhenden Wagen haben wir nur zwei Kräfte, die Schwerkraft
und die Zentrifugalkraft durch
die Rotation der Erde:
Die Gesamtkraft ist also:
b) Fährt der Wagen, kommt die Zentrifugalkraft der Bewegung des Wagens und die Coriolis- Kraft hinzu:
Hierbei ist 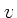 die Geeschwindigkeit des Wagens in Bezug auf die Erdoberfläche. Die Vorzeichen ergeben
sich aus der Tatsache, daß die Erde nach nach Osten rotiert.
die Geeschwindigkeit des Wagens in Bezug auf die Erdoberfläche. Die Vorzeichen ergeben
sich aus der Tatsache, daß die Erde nach nach Osten rotiert.
c) Jetzt muß gelten:
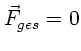 .
.
Auflösen dieser Gleichung nach 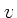 ergibt:
ergibt:
Ohne die Coriolis- Kraft hätte man einen Wert
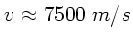 erhalten.
erhalten.
Aus 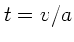 folgt
folgt
Harm Fesefeldt
2007-08-06

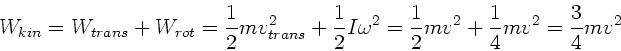
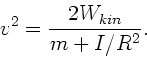

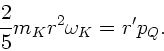
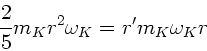
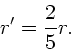
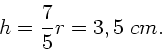
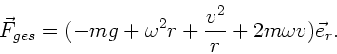
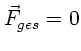 .
.