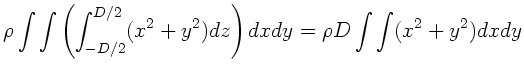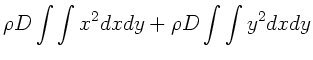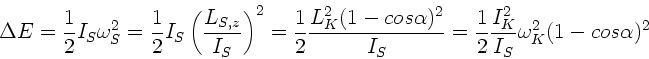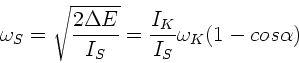Physik I, WS 1993/94
Lösungen zur Übung Nr. 6
Besprechung: 9. Dezember 1993
Aufgabe 1: (4 Punkte)
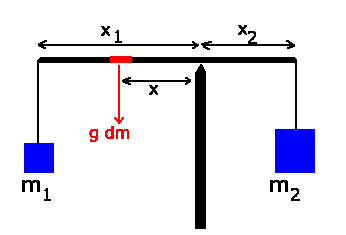
Wir bezeichnen mit 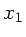 und
und 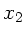 die Unterteilung der Stange, sodaß
also
die Unterteilung der Stange, sodaß
also 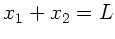 ist. Das Drehmoment eines infinitesimalen
Massenelements
ist. Das Drehmoment eines infinitesimalen
Massenelements 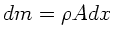 , mit Querschnit
, mit Querschnit 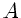 und Dichte
und Dichte 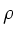 , ist
also
, ist
also
Daraus folgt, zusammen mit den beiden Massen 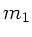 und
und  :
:
Im Gleichgewicht muß
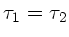 sein, daher
sein, daher
Elimination von
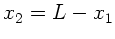 ergibt:
ergibt:
oder
Einsetzen der Masse 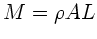 der Stange ergibt das Endergebnis
der Stange ergibt das Endergebnis
Entsprechend folgt aus Symmetriegründen:
Zahlenwerte:
Aufgabe 2: (6 Punkte)
a) Der Drehimpuls vor dem Aufprall ist 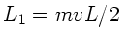 , der Drehimpuls nach
dem Aufprall
, der Drehimpuls nach
dem Aufprall
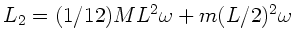 , wobei wir
das Trägheitsmoment
, wobei wir
das Trägheitsmoment
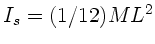 einer homogenen Stange aus
der Vorlesung übernommen haben. Drehimpulserhaltung ergibt:
einer homogenen Stange aus
der Vorlesung übernommen haben. Drehimpulserhaltung ergibt:
Zahlenwerte:
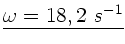 .
.
b) Falls die Achse nicht durch den Mittelpunkt verläuft, gilt nach dem
Steinerschen Satz für den Drehimpuls nach dem Stoß:
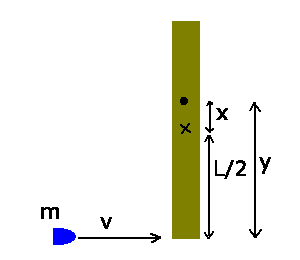
Gleichsetzen der Drehimpulse vor und nach dem Stoß führt jetzt auf:
Die Extremalbedingung
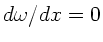 ergibt nach einiger Rechnung:
ergibt nach einiger Rechnung:
Einsetzen der Zahlenwerte ergibt
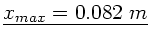 . Der
Wert liegt also nur unwesentlich von der Stangenmitte entfernt.
Die Winkelgeschwindigkeit im Maximum ist
. Der
Wert liegt also nur unwesentlich von der Stangenmitte entfernt.
Die Winkelgeschwindigkeit im Maximum ist
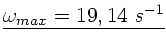 .
.
Aufgabe 3: (6 Punkte)
Wir zerlegen den Kreiskegel in Scheiben der Dicke 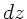 und Radius
und Radius
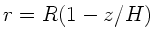 . Die Masse einer Kreisscheibe ist
. Die Masse einer Kreisscheibe ist
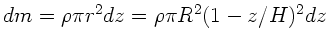 . Die Masse
des gesamten Kreiskegels ist
. Die Masse
des gesamten Kreiskegels ist
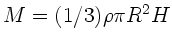 .
.
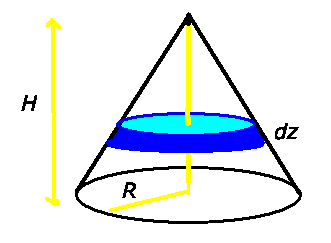
a) Aus Symmetriegründen liegen die 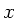 - und
- und 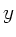 - Koordinaten des
Schwerpunktes bei
- Koordinaten des
Schwerpunktes bei 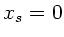 und
und 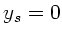 . Für die
. Für die 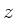 - Koordinate
folgt nach Definition:
- Koordinate
folgt nach Definition:
Ausgedrückt mit der Gesamtmasse folgt:
b) Das Trägheitsmoment einer Kreisscheibe ist nach Vorlesung
Integration von 0 bis 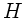 ergibt
ergibt
Aufgabe 4: (Bonusaufgabe) (10 Punkte)
a) Bei der 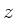 - Achse als Rotationsachse ist
- Achse als Rotationsachse ist
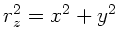 und damit
und damit
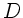 ist hierbei die Dicke der Platte.
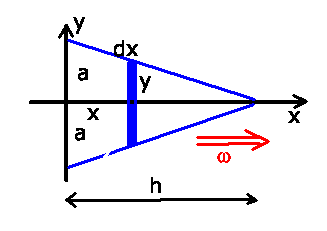
Das gleiche Ergebnis erhält man auch leicht mit Hilfe des Steinerschen
Satzes. Wir unterteilen das Dreieck in infinitesimale dünne Stangen:
ist hierbei die Dicke der Platte.
Das gleiche Ergebnis erhält man auch leicht mit Hilfe des Steinerschen
Satzes. Wir unterteilen das Dreieck in infinitesimale dünne Stangen:
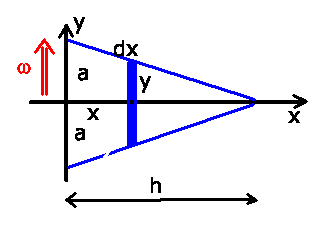
Eine Stange hat die Masse
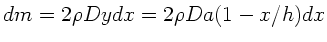 und
Länge
und
Länge
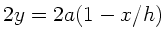 . Das Trägheitsmoment einer dünnen Stange der
Länge
. Das Trägheitsmoment einer dünnen Stange der
Länge 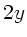 , deren Rotationsachse den Abstand
, deren Rotationsachse den Abstand 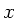 vom Schwerpunkt der
Stange hat, ist nach Vorlesung
vom Schwerpunkt der
Stange hat, ist nach Vorlesung
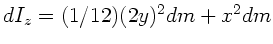 .
Daher
.
Daher
Dieses ist offensichtlich dasselbe Ergebnis wie oben. Dieses Integral wird
gelöst durch (mit 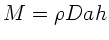 )
)
b) Bei Rotation um die 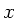 - Achse gilt entsprechend:
- Achse gilt entsprechend:
Mit 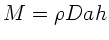 folgt:
folgt:
Bei Rotation um die 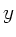 - Achse:
- Achse:
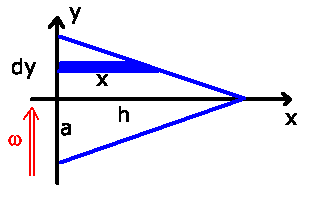
Hier ist aber jetzt
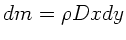 und
und 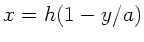 . Daher
. Daher
Damit haben wir die Beziehung
verifiziert.
c) Bei der allgemeinen Beweisführung kommt man natürlich an den
dreidimensionalen Integralen nicht vorbei. Es ist
Das Trägheitsmoment 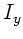 läßt sich schreiben als
läßt sich schreiben als
oder
Nach Vorraussetzung ist aber 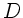 klein gegenüber
klein gegenüber 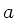 und
und 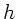 , daher
kann der Term mit
, daher
kann der Term mit 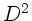 vernachlässigt werden. Wir erhalten also
vernachlässigt werden. Wir erhalten also
Analog:
Dann ist aber
Aufgabe 5: (4 Punkte)
Zu Beginn sei der Drehimpuls des Kreisels
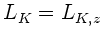 in Richtung der
in Richtung der
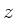 - Achse. Bei Drehung der Kreiselachse um den Winkel
- Achse. Bei Drehung der Kreiselachse um den Winkel 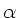 wird
die
wird
die 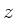 - Komponente verkleinert zu
- Komponente verkleinert zu
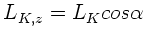 . Die Differenz
. Die Differenz
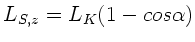 wird auf den Stuhl übertragen. Die anderen
Komponenten des Drehimpulses werden von den Stuhlhalterungen und der
Physikerin abgefangen. Die kinetische Energie des Kreisels bleibt bei der
Drehung der Kreiselachse erhalten. Die Änderung der kinetischen Energie
wird allein durch die Drehung des Stuhls verursacht:
wird auf den Stuhl übertragen. Die anderen
Komponenten des Drehimpulses werden von den Stuhlhalterungen und der
Physikerin abgefangen. Die kinetische Energie des Kreisels bleibt bei der
Drehung der Kreiselachse erhalten. Die Änderung der kinetischen Energie
wird allein durch die Drehung des Stuhls verursacht:
Die Winkelgeschwindigkeit des Stuhls ergibt sich zu
Einsetzen der Zahlenwerte führt auf die folgende Tabelle:
![$\alpha \; [Grad]$](img92.gif) |
![$\Delta E \; [J]$](img93.gif) |
![$\omega \; [s^{-1}]$](img94.gif) |
| |
|
|
| 45 |
0.00057 |
0.020 |
| 90 |
0.0067 |
0.067 |
| 135 |
0.019 |
0.11 |
| 180 |
0.027 |
0.13 |
Harm Fesefeldt
2007-08-06

![]() und
und ![]() :
:
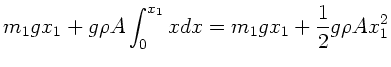
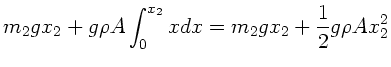
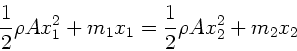
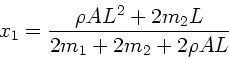
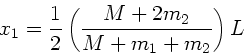
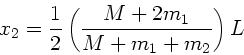
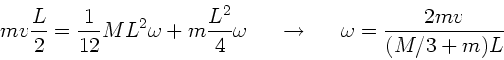
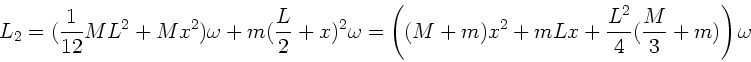

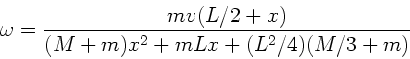
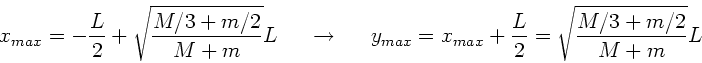

![]() - und
- und ![]() - Koordinaten des
Schwerpunktes bei
- Koordinaten des
Schwerpunktes bei ![]() und
und ![]() . Für die
. Für die ![]() - Koordinate
folgt nach Definition:
- Koordinate
folgt nach Definition:
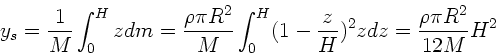
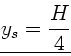
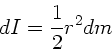
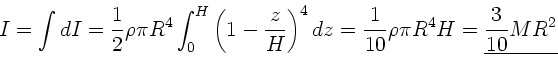
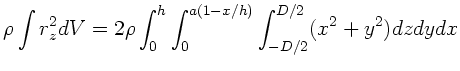
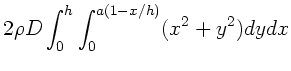
![$\displaystyle 2\rho D \int_{0}^{h} \left[ x^{2} a (1-\frac{x}{h})
+ \frac{1}{3} a^{3} (1-\frac{x}{h})^{3} \right] dx$](img53.gif)

![]() und
Länge
und
Länge
![]() . Das Trägheitsmoment einer dünnen Stange der
Länge
. Das Trägheitsmoment einer dünnen Stange der
Länge ![]() , deren Rotationsachse den Abstand
, deren Rotationsachse den Abstand ![]() vom Schwerpunkt der
Stange hat, ist nach Vorlesung
vom Schwerpunkt der
Stange hat, ist nach Vorlesung
![]() .
Daher
.
Daher
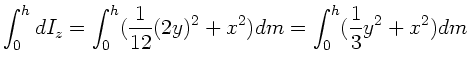
![$\displaystyle 2\rho D \int_{0}^{h} \left[ x^{2} a (1-\frac{x}{h})
+ \frac{1}{3} a^{3} (1-\frac{x}{h})^{3} \right] dx$](img53.gif)
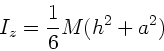

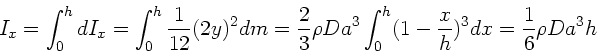
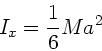

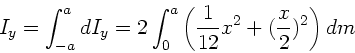
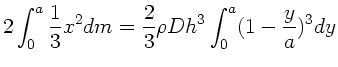
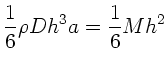
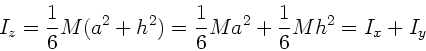
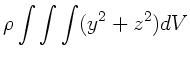
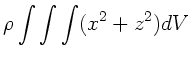
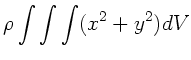
![\begin{displaymath}
I_{y} = \rho \int \int \left( \int_{-D/2}^{D/2} (x^{2}+z^{2...
...eft[ x^{2} z + \frac{1}{3}
z^{3} \right]_{-D/2}^{D/2} dx dy
\end{displaymath}](img76.gif)