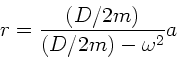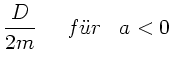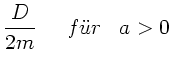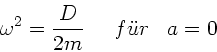Physik I, WS 1993/94
Lösungen zur Übung Nr. 5
Besprechung: 2. Dezember 1993
Aufgabe 1: (4 Punkte)
Lösung:
Aufgabe 2: (5 Punkte)
a) Die Geschwindigkeit im Punkt 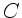 muß mindestens so groß sein, daß die
Zentrifugalkraft
muß mindestens so groß sein, daß die
Zentrifugalkraft
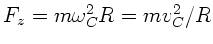 der
Schwerkraft
der
Schwerkraft 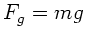 entgegengesetzt gleich ist, also:
entgegengesetzt gleich ist, also:
Die Geschwindigkeit als Funktion der Anfangshöhe folgt aus der
totalen Energiebilanz:
Daher:
b) Sei nun 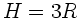 , dann ist die Geschwindigkeit in A,B,C und D wegen
Energieerhaltung:
, dann ist die Geschwindigkeit in A,B,C und D wegen
Energieerhaltung:
Dieses ergibt der Reihe nach:
c) Die Kraft ist jeweils die Vektorsumme von Zentrifugalkraft und
Schwerkraft, also:
Aufgabe 3: (5 Punkte)
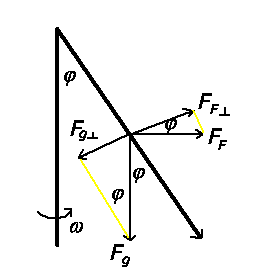
a) Aus der Abbildung folgt:
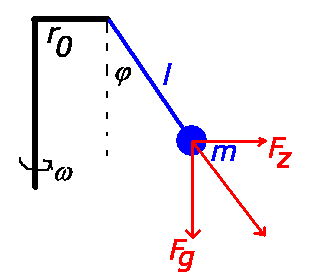
Dieses ist eine transzendente Gleichung, die wir graphisch lösen:
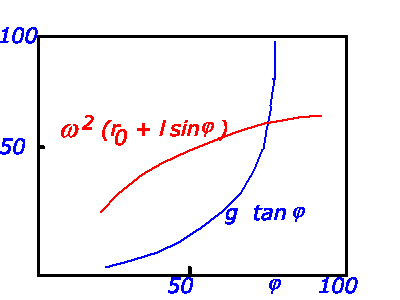
Die Lösung ist
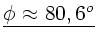 .
.
b) Für 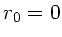 ist
ist
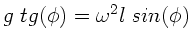 oder
oder
In dieser Formel ist 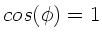 und damit
und damit 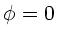 für die Grenzfrequenz
für die Grenzfrequenz
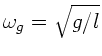 . Für
. Für
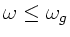 hat das System
keinen festen Ausschlagwinkel, da die Komponente der Schwerkraft senkrecht
zum Pendel grundsätzlich größer wird als die Komponente der Fliehkraft
hat das System
keinen festen Ausschlagwinkel, da die Komponente der Schwerkraft senkrecht
zum Pendel grundsätzlich größer wird als die Komponente der Fliehkraft
Mit
gilt für
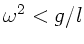 die Abschätzung:
die Abschätzung:
Merkwürdigerweise ist
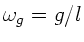 aber gerade die Frequenz
der linearen Pendelbewegung. Die Rotationsfrequenz ist also in Resonanz
mit der Kreisfrequenz der linearen Pendelbewegung.
aber gerade die Frequenz
der linearen Pendelbewegung. Die Rotationsfrequenz ist also in Resonanz
mit der Kreisfrequenz der linearen Pendelbewegung.
Aufgabe 4: (6 Punkte)
Für 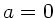 befindet sich der Wagen auf der Drehachse, wenn die Feder in
Ruhelage ist, für
befindet sich der Wagen auf der Drehachse, wenn die Feder in
Ruhelage ist, für 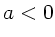 ist die Feder vorgespannt und für
ist die Feder vorgespannt und für 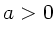 ist die
Feder bei
ist die
Feder bei 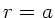 in Ruhelage. Allgemein gilt:
in Ruhelage. Allgemein gilt:
Für 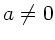 folgt:
folgt:
mit positiven, von Null und unendlich verschiedenen Werten für 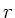 bei:
bei:
Für 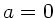 schließlich gibt es nur eine von Null und Unendlich
verschiedene Lösung für
schließlich gibt es nur eine von Null und Unendlich
verschiedene Lösung für 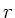 , falls
, falls
a) Damit ergibt sich die folgende Skizze der möglichen Werte für 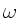 und
und 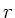 bei den 3 Fallunterscheidungen für
bei den 3 Fallunterscheidungen für 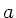 :
:
b) Für 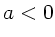 und
und
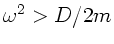 existiert zwar ein Gleichgewicht,
jedoch ist die Lage der Wagen grundsätzlich instabil.
Bei größerem
existiert zwar ein Gleichgewicht,
jedoch ist die Lage der Wagen grundsätzlich instabil.
Bei größerem 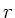 ist
ist 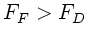 , dh. wir haben keine Rückstellkraft,
die Wagen laufen nach unendlich.
, dh. wir haben keine Rückstellkraft,
die Wagen laufen nach unendlich.
c) Eine stabile Lage und damit einen Fliehkraftregler mit 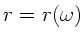 erhält man nur für
erhält man nur für 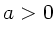 und
und
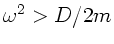 .
.
d) Für 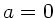 und
und
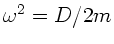 ist die Lage der Wagen bei jedem
ist die Lage der Wagen bei jedem 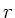 stabil.
stabil.
Harm Fesefeldt
2007-08-06
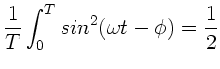
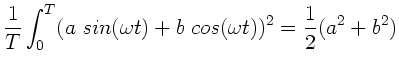
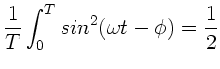
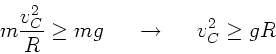
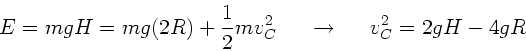
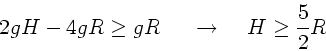
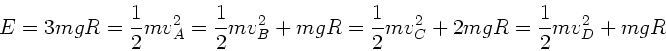
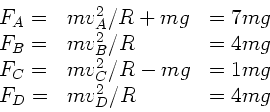

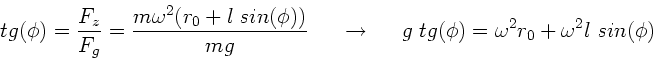

![]() .
. ![]() ist
ist
![]() oder
oder
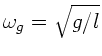 . Für
. Für