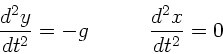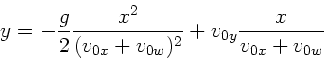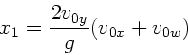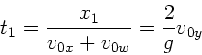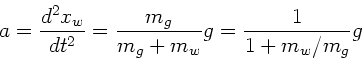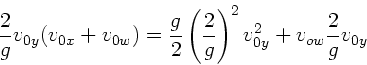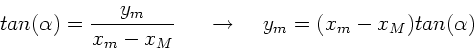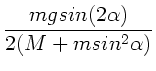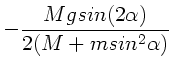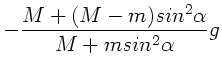Physik I, WS 1993/94
Lösungen zur Übung Nr. 2
Besprechung: 11. November 1993
Aufgabe 1: (4 Punkte)
Wir benutzen die in der folgenden Abbildung angegebenen Bezeichnungen.
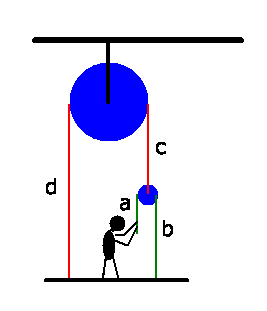
Wegen
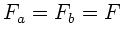 und
und
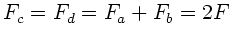 folgt die Gleichgewichtsbedingung
folgt die Gleichgewichtsbedingung
a) Daraus folgt 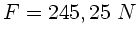 . Der Arbeiter drückt mit der Kraft
. Der Arbeiter drückt mit der Kraft
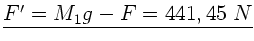 auf die Plattform.
auf die Plattform.
b) Das Maximum folgt aus 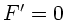 . Wegen
. Wegen 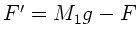 liegt das Maximum
also bei
liegt das Maximum
also bei 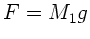 . Daraus folgt:
. Daraus folgt:
Also:
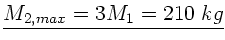 .
.
Aufgabe 2: (4 Punkte)
Die Feder wird in zwei gleich große Teile unterteilt,
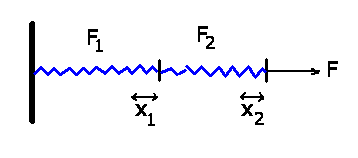
dann ist
Wegen
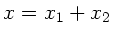 folgt:
folgt:
Vergleich mit erster Gleichung liefert
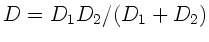 .
Da in unserem Fall
.
Da in unserem Fall
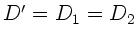 , folgt sofort
, folgt sofort
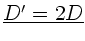 .
.
b) Übt man auf dieses System eine Kraft 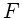 aus, so ist diese die Summe
aus den an den einzelnen Federn angreifenden Kräften. Also:
aus, so ist diese die Summe
aus den an den einzelnen Federn angreifenden Kräften. Also:
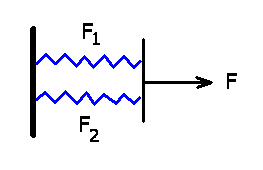
Die Federkonstante des Gesamzsystems ist also
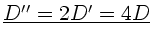 .
.
Aufgabe 3: (6 Punkte)
Der Abschuß der Kugel sei zur Zeit 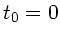 . Die Geschwindigkeit des
Wagens zur Zeit
. Die Geschwindigkeit des
Wagens zur Zeit 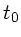 sei
sei 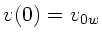 . Die Bewegungsgleichungen
der Kugel sind dann
. Die Bewegungsgleichungen
der Kugel sind dann
Lösung mit bekannten Anfangsbedingungen:
Wir setzen die Koordinate des Abschusses
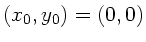 und erhalten
aus der zweiten Gleichung
und erhalten
aus der zweiten Gleichung
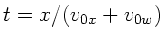 . Eingesetzt in die erste
Gleichung ergibt:
. Eingesetzt in die erste
Gleichung ergibt:
Dieses ist ein Parabel, die die y-Achse bei 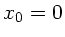 (Abschuß) und bei
(Abschuß) und bei
schneidet. Die Zeit des zweiten Schnittpunktes folgt aus
Die allgemeine Wagenbewegung hatten wir bereits in den Rechenübungen
am 28.10.93 studiert. Die Beschleunigung war
a) Sei zunächst 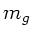 sehr viel größer als
sehr viel größer als 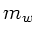 , dann folgt
aus
, dann folgt
aus
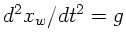 , daß
, daß
Zur Zeit 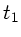 (siehe oben) soll
(siehe oben) soll 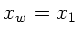 sein,
sein,
oder :
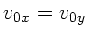 . Der Abschußwinkel ist also
. Der Abschußwinkel ist also
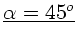 .
.
b) Für 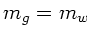 folgt
folgt
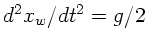 (siehe oben).
Mit entsprechender Rechnung wie in a) folgt die Bedingung
(siehe oben).
Mit entsprechender Rechnung wie in a) folgt die Bedingung
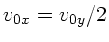 . In diesem Fall muß der Abschußwinkel also
. In diesem Fall muß der Abschußwinkel also
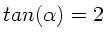 oder
oder
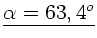 sein.
sein.
Aufgabe 4: (6 Punkte)
In der folgenden Abbildung sind die Kräfte eingezeichnet. Die Masse
des Keils sei 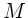 , die Masse des Körpers
, die Masse des Körpers 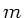 .
.
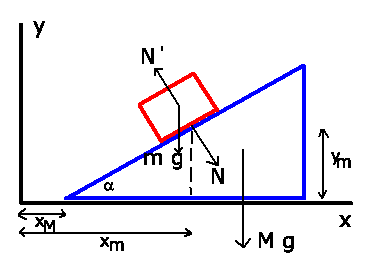
Dann gilt
Wegen 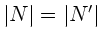 folgen hieraus zwei Zwangsbedingungen für die
drei Komponenten der Beschleunigungen
folgen hieraus zwei Zwangsbedingungen für die
drei Komponenten der Beschleunigungen
Die notwendige dritte Zwangsbedingung erhält man folgendermaßen.
Wir setzen die Koordinaten von Körper und Keil wie in der folgenden
Abbildung:
Dann gilt:
Zweimalige Ableitung dieser Gleichung führt auf die dritte Bedingung
für die Beschleunigungen
Die Lösung dieser drei Gleichungen ergibt, sofern ich mich nicht
verrechnet habe:
Harm Fesefeldt
2007-08-06


![]() und
und
![]() folgt die Gleichgewichtsbedingung
folgt die Gleichgewichtsbedingung

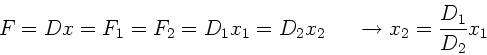
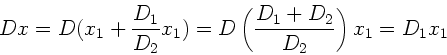

![]() .
.
![]() . Die Geschwindigkeit des
Wagens zur Zeit
. Die Geschwindigkeit des
Wagens zur Zeit ![]() sei
sei ![]() . Die Bewegungsgleichungen
der Kugel sind dann
. Die Bewegungsgleichungen
der Kugel sind dann