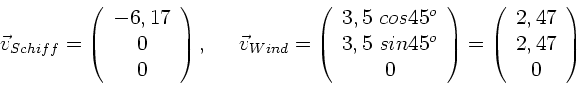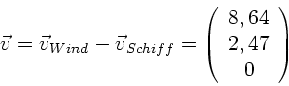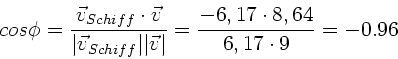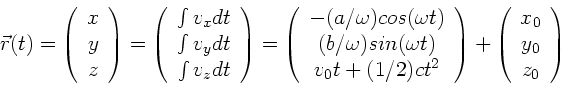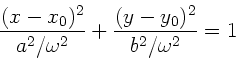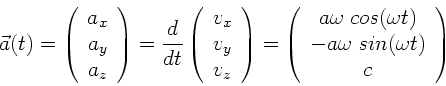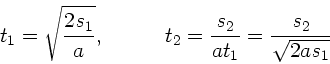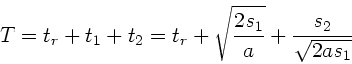Physik I, WS 1993/94
Lösungen zur Übung Nr. 1
Besprechung: 4. November 1993
Aufgabe 1: (5 Punkte)
Die Dimensionen müssen auf beiden Seiten der Gleichungen übereinstimmen.
Dieses ergibt:
a)
Also: n=2 und j=1.
b)
Also: n=1, j=-1 und i=1.
c) Das Argument der Sinusfunktion muß dimensionslos sein. Dieses ergibt
zunächst
Der Faktor vor der Sinusfunktion muß die Dimension einer Länge haben:
Also: n=1 , j=2, l=-1 und
i=-2.
Aufgabe 2: (5 Punkte)
Bei der Umrechnung von Knoten in km/h bzw m/s muß zwischen
Landmeile und nautischer Meile unterschieden werden:
Bei der Einheit 'Knoten' handelt es sich offensichtlich um die nautische
Meile. Daher:
Koordinatensystem mit x-Achse nach Osten und y-Achse nach Norden:
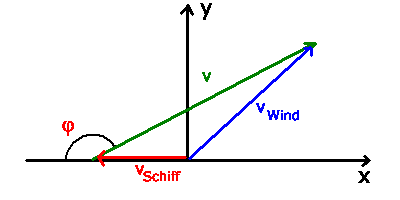
Schiff und Wind haben die Geschwindigkeitsvektoren (in Einheiten von m/s)
Der auf dem Schiff gemessene scheinbare Wind ist
Daraus folgt:
![$\underline{\vert\vec{v}\vert \approx 9 \left[ m/s \right]}$](img24.gif) .
.
Das Skalarprodukt beider Vektoren ist:
Der Winkel zwischen scheinbarem Wind und Fahrtrichtung ist damit:
Also:
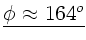
Aufgabe 3: (5 Punkte)
a) Gesucht ist
Wegen
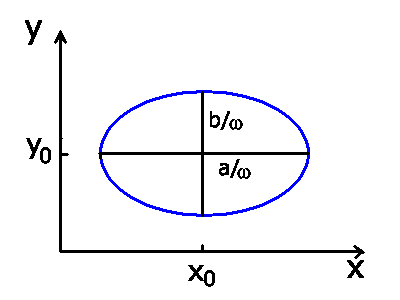
ergibt die Projektion auf die x-y Ebene eine Ellipse mit den Achsen
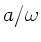 und
und 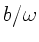 und dem Mittelpunkt
und dem Mittelpunkt
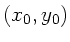 .
.
b) Die Beschleunigung ist
Der Körper wird insbesondere in z- Richtung mit konstanter Beschleunigung
bewegt.
Aufgabe 4: (5 Punkte)
Mit
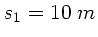 und
und
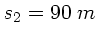 gilt:
gilt:
und damit:
Die Gesamtzeit ist, mit der Reaktionszeit 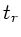 :
:
Einsetzen der Zahlenwerte führt auf
Die Gesamtzeit ist also unter 10 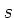 , sofern die Reaktionszeit unter
, sofern die Reaktionszeit unter
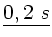 bleibt.
bleibt.
Harm Fesefeldt
2007-08-06
![$\displaystyle \left[ \frac{m}{s} \right]^{n}$](img1.gif)
![$\displaystyle k \left[ \frac{m}{s^{2}}
\right]^{j} \left[ m \right]$](img3.gif)
![$\displaystyle \left[ \frac{m^{n-j-1}}{s^{n-2j}} \right]$](img5.gif)
![$\displaystyle \left[ \frac{m}{s} \right]^{n}$](img1.gif)
![$\displaystyle k \left[ \frac{m}{s^{2}}
\right]^{j} \left[ m \right]$](img3.gif)
![$\displaystyle \left[ \frac{m^{n-j-1}}{s^{n-2j}} \right]$](img5.gif)
![$\displaystyle \left[ \frac{m}{s^{2}} \right]^{n} \left[ \frac{m}{s} \right]^{j}
\left[ s \right]^{i}$](img9.gif)
![$\displaystyle \left[ \frac{m^{n+j}}{s^{2n+j-i}} \right]$](img10.gif)
![$\displaystyle \left[ m \right] \left[ s \right]^{i} \left[ \frac{m}{s^{2}} \right]^{l}$](img13.gif)
![$\displaystyle \left[ \frac{m}{s^{2}} \right]^{n} \left[ s
\right]^{j}$](img17.gif)
![\begin{displaymath}
12 \; Knoten = 12 \cdot 1.85 \left[ \frac{km}{h} \right] = 6,17 \left[
\frac{m}{s} \right]
\end{displaymath}](img21.gif)