Physik III, WS 1992/93
Rechenübungen am 9. Dezember 1992
Optische Instrumente
In der Übungsstunde am 2.12.92 wurden die Grundlagen der
paraxialen Matrizen- Optik eingeführt. In dieser Übungsstunde
werden wir dieses Verfahren benutzen, um einfache optische
Geräte zu studieren. Wir wiederholen kurz die wichtigsten
Transformationen.
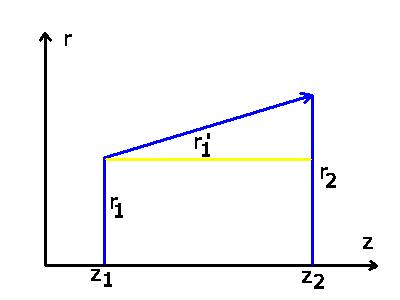
1) Ein Lichtstrahl mit Abstand 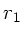 und Winkel
und Winkel 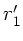 zur optischen Achse wird von
Punkt
zur optischen Achse wird von
Punkt 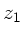 nach Punkt
nach Punkt 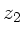 transformiert (
transformiert (
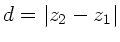 ):
):
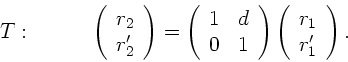 |
(1) |
2) Ein sphärischer Spiegel läßt den Abstand 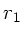 zur optischen
Achse konstant (
zur optischen
Achse konstant (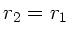 ) und ändert nur die Richtung
) und ändert nur die Richtung
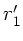 nach
nach 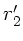 :
:
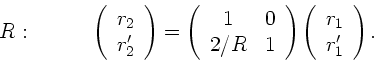 |
(2) |
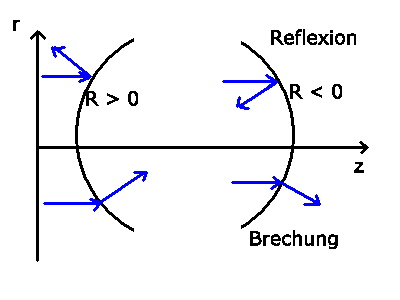
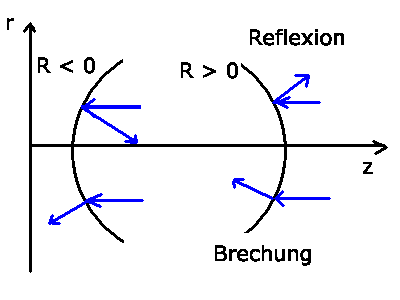
3) Eine spärische Begrenzungsfläche zwischen zwei Medien mit den
Brechungsindizes 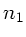 und
und 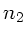 läßt den Abstand zur
optischen Achse ebenfalls konstant, ändert aber die Richtung des
Lichtstrahls. Der Strahl läuft von Medium 1 nach Medium 2:
läßt den Abstand zur
optischen Achse ebenfalls konstant, ändert aber die Richtung des
Lichtstrahls. Der Strahl läuft von Medium 1 nach Medium 2:
Um die Brechkraft einer einzelnen Bregrenzungsfläche von der Brechkraft
der Linse (siehe später) zu unterscheiden, führen wir ab jetzt die
Bezeichnung 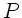 ein. In der letzten Übung hatten wir hierfür
ebenfalls das Symbol
ein. In der letzten Übung hatten wir hierfür
ebenfalls das Symbol 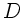 benutzt.
benutzt.
4) Mit Hilfe dieser drei Transformationen kann man die
Transformations- Matrix einer Linse herleiten (siehe Beispiel 3 der
Übungsstunden vom 2.12.92).
Für die dünne Linse (Dicke der
Linse 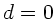 ) erhält man (siehe auch Vorlesung und Aufgabe 1 dieser
Übung):
) erhält man (siehe auch Vorlesung und Aufgabe 1 dieser
Übung):
Hierbei haben wir die allgemeinste Form angeschrieben. Die Linse
begrenzt zwei Medien mit Brechungsindex 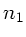 und
und 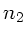 , der
Brechungsindex des Linsenmaterials selbst ist
, der
Brechungsindex des Linsenmaterials selbst ist 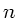 . Die
Krümmungsradien der Linsenflächen sind
. Die
Krümmungsradien der Linsenflächen sind 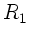 und
und 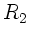 .
Der Lichtstrahl läuft von Medium 1 durch die Linse in das Medium 2.
.
Der Lichtstrahl läuft von Medium 1 durch die Linse in das Medium 2.
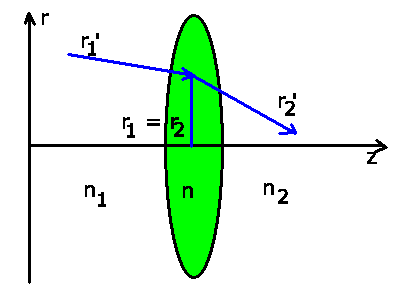
Vorzeichenkonvention für die Krümmungsradien
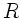 ist positiv, wenn die Krümmung von der Richtung des
Lichtstrahls
aus gesehen konvex ist,
ist positiv, wenn die Krümmung von der Richtung des
Lichtstrahls
aus gesehen konvex ist, 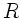 ist negativ,
wenn die Krümmung von der
Richtung des Lichtstrahls aus gesehen konkav ist.
ist negativ,
wenn die Krümmung von der
Richtung des Lichtstrahls aus gesehen konkav ist.
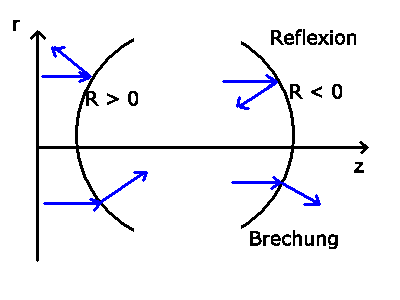
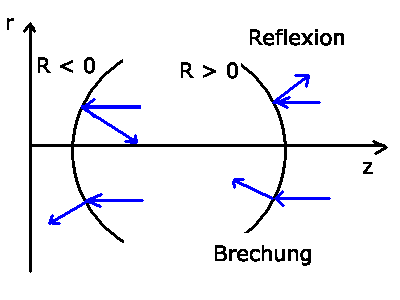
- Diese Vorzeichenkonvention ist für die Brechung
und für die Linsen identisch mit der in der Vorlesung
gewählten Konvention, für die Reflektion dagegen gerade umgekehrt.
In der Vorlesung wurde das Vorzeichen im Hinblick auf die
Realität und Virtualität von Abbildungen gewählt. Hiernach
muß man bei der Reflektion an konkaven Flächen ein positives
Vorzeichen, bei der Reflektion an konvexen Flächen ein negatives
Vorzeichen wählen. In der Matrizen- Optik dagegen kann es zu
schlimmen Fehlern führen, wenn man verschiedene Vorzeichen
für Reflektion und Brechung an ein und derselben Wölbung einführt,
insbesondere dann, wenn man Spiegel und Linsen in ein- und
derselben optischen Anordnung hat (z.B. bei Spiegellinsen).
Wer die in der Vorlesung benutzte Vorzeichenkonvention vorzieht,
muß in der Transformationsmatrix der Reflexion
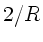 durch
durch
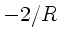 ersetzen.
ersetzen.
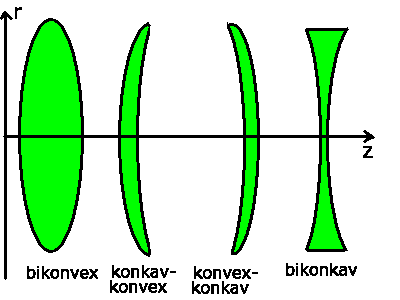
- In der technischen Literaur weicht die Bezeichnung für Linsen
von dem hier gewählten Schema ab. Eine Bikonvex- Linse ist z.B. eine
Linse mit einer konvexen und einer konkaven Begrenzungsfläche. Bei der
Bezeichnung von Linsen ist nicht entscheidend, welche Wölbung der
Lichtstrahl sieht, sondern welche Wölbung man jeweils von außen
sieht. Im folgenden sind die technischen Bezeichnungen noch einmal
aufgeführt.
Im übrigen ist es empfehlenswert, die Vorzeichen von 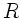 bereits
bei der Aufstellung der Transformationen einzusetzen, sodaß in den
Rechnungen selbst
bereits
bei der Aufstellung der Transformationen einzusetzen, sodaß in den
Rechnungen selbst 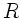 stets positiv ist.
Schließlich sollte noch erwähnt werden, daß die Transformationen
der Brechung und Reflexion auch für den Grenzfall
stets positiv ist.
Schließlich sollte noch erwähnt werden, daß die Transformationen
der Brechung und Reflexion auch für den Grenzfall  gelten, d.h. auch für ebene Begrenzungsflächen gültig sind.
gelten, d.h. auch für ebene Begrenzungsflächen gültig sind.
Durch Mehrfachanwendung kann man mit Hilfe dieser drei Transformationen
den Strahlengang in
beliebig komplizierten Systeme berechnen.
In dieser Übung betrachten wir die wichtigsten, aus zwei dünnen
Linsen bestehenden Systeme.
- Aufgabe 1:
Zeigen Sie, daß die oben angegebene Transformationsmatrix für
die dünne Linse aus der Transformationsmatrix der Brechung folgt.
- Aufgabe 2:
Unter welche Bedingungen ist bei einer einzigen Linse der
Strahlengang vertauschbar, d.h. wann ist es für die Abbildung
egal, Vorder- und Rückseite der Linse zu vertauschen ?
Systeme aus zwei Linsen.
Wir betrachten ein System aus zwei dünnen Linsen, die sich auf der
optischen Achse im Abstand 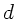 befinden.
befinden.
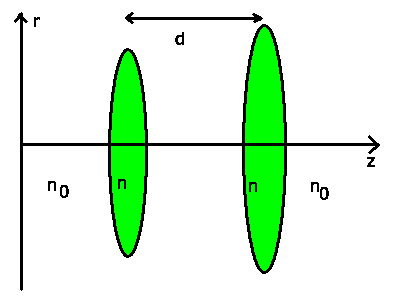
Hierbei kann es sich um
belibig gewölbte Linsen handeln. Das umgebende Material sei ein
Material mit Brechungsindex 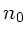 (d.h.
(d.h.
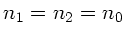 in der
Linsenmatrix),
das Linsenmaterial sei immer Glas mit Brechungsindex
in der
Linsenmatrix),
das Linsenmaterial sei immer Glas mit Brechungsindex 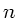 .
Dann erhalten wir für die Brechkräfte der Linsen:
.
Dann erhalten wir für die Brechkräfte der Linsen:
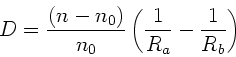 |
(3) |
Beachten Sie hierbei aber sorgfältig die Vorzeichenkonvention für
die Krümmungsradien. Diese sind in der nachfolgenden Skizze
noch einmal für die verschiedenen Linsentypen angegeben,
und zwar einmal für Lichtstrahlen in Richtung der optischen Achse (oben),
zum anderen für Lichtstrahlen entgegengesetzt zur optischen Achse
(unten).
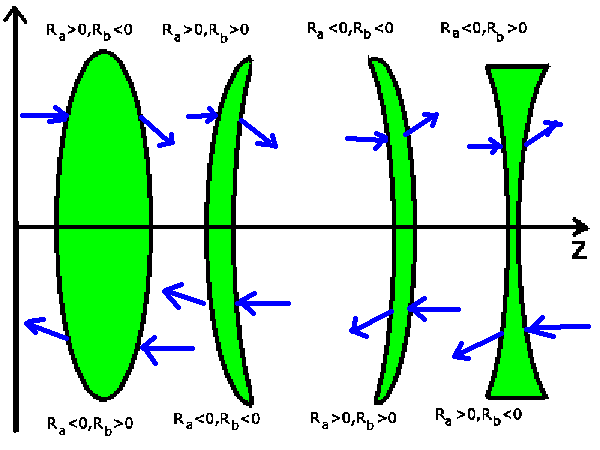
Abbildung durch einen zweistufigen Prozeß.
In Lehrbüchern (siehe auch Vorlesung)
wird die Abbildung durch ein System zweier Linsen
gewöhnlich als zweistufiger Prozeß dargestellt. Dazu wird zunächst
das von der ersten Linse entworfene Zwischenbild bestimmt. Dieses
Zwischenbild wird dann mit der zweiten Linse zum Endbild
abgebildet. Die folgende Skizze zeigt das Verfahren.
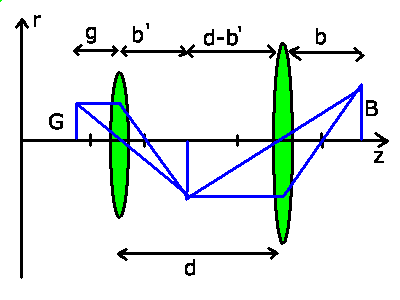
Offensichtlich gilt
Elimination von 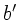 aus beiden Gleichungen führt dann zu
der gesuchten Abbildungsgleichung zwischen
aus beiden Gleichungen führt dann zu
der gesuchten Abbildungsgleichung zwischen 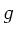 und
und 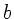 .
Ähnlich kann der Abbildungsmaßtab aus einem derartigen
zweistufigen Prozeß berechnet werden. Bei Systemen mit
mehr als zwei Linsen wird dieses Verfahren aber außerordentlich
mühsam, wenn nicht sogar unlösbar. Systeme mit vielen
Abbildungselementen werden
in der Lasertechnik (z.B. optische Resonatoren) und in der Teilchenoptik
(Elektronenmikroskope, Beschleuniger) benötigt. Im letzteren Fall
handelt es sich natürlich nicht um optische, sondern um
elektrische und magnetische Linsen. Derartige Systeme können
nur mit den Methoden der Matrizen- Optik behandelt werden.
Als Übung hierzu wollen wir auch das zweistufe Linsensystem
mit der Matrizen- Optik behandeln.
.
Ähnlich kann der Abbildungsmaßtab aus einem derartigen
zweistufigen Prozeß berechnet werden. Bei Systemen mit
mehr als zwei Linsen wird dieses Verfahren aber außerordentlich
mühsam, wenn nicht sogar unlösbar. Systeme mit vielen
Abbildungselementen werden
in der Lasertechnik (z.B. optische Resonatoren) und in der Teilchenoptik
(Elektronenmikroskope, Beschleuniger) benötigt. Im letzteren Fall
handelt es sich natürlich nicht um optische, sondern um
elektrische und magnetische Linsen. Derartige Systeme können
nur mit den Methoden der Matrizen- Optik behandelt werden.
Als Übung hierzu wollen wir auch das zweistufe Linsensystem
mit der Matrizen- Optik behandeln.
Abbildung mit Hilfe der Matrizen-Optik.
Die Transformation eines Lichtstrahls vom Punkt 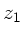 zum
Punkt
zum
Punkt 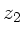 ist gegeben durch
ist gegeben durch
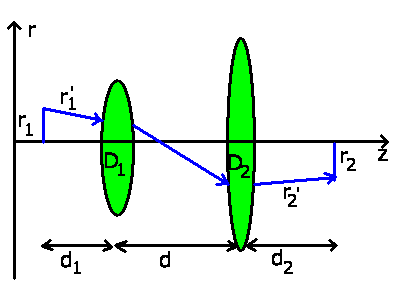
Die Systemmatrix 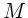 läßt sich leicht auswerten und ergibt:
läßt sich leicht auswerten und ergibt:
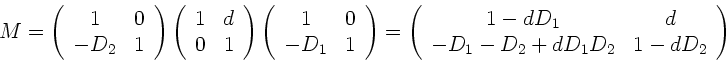 |
(4) |
Die Elemente der Matrix 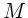 sind also:
sind also:
- Aufgabe 3:
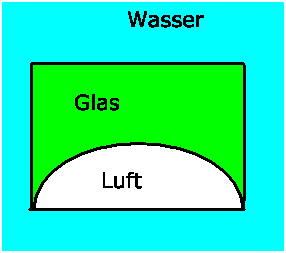
Eine dünne, plankonkave Linse (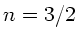 ) ist in horizontaler Stellung so
in Wasser (
) ist in horizontaler Stellung so
in Wasser (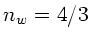 ) getaucht, daß der unter der sphärischen Fläche
liegende Raum mit Luft (
) getaucht, daß der unter der sphärischen Fläche
liegende Raum mit Luft (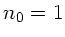 ) gefüllt ist. Die Gesamtbrechkraft
des optischen Systems hat den
Wert
) gefüllt ist. Die Gesamtbrechkraft
des optischen Systems hat den
Wert
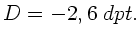 Bestimmen Sie den Krümmungsradius der Linse.
Betrachten Sie hierbei das System
Bestimmen Sie den Krümmungsradius der Linse.
Betrachten Sie hierbei das System
a) einmal als zentriertes System zweier Linsen (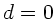 ),
),
b) zum anderen als Einzellinse aus drei brechenden Flächen.
Die gesamte Transformation läßt sich ausrechnen zu (siehe
auch Beispiel 3 der Übungen vom 2.12.92):
Zur Bestimmung der Abbildungsgleichung setzen wir 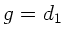 ,
, 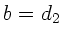 und fordern, daß jeder von
und fordern, daß jeder von 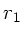 kommende Lichtstrahl in
kommende Lichtstrahl in 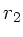 fokussiert wird, unabhängig von
fokussiert wird, unabhängig von 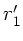 . Dann muß der
Koeffizient vor
. Dann muß der
Koeffizient vor 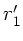 in der ersten der beiden Transformationsformeln
verschwinden:
in der ersten der beiden Transformationsformeln
verschwinden:
Hieraus folgen die Abbildungsgleichungen
Den Abbildungsmaßstab erhält man hieraus zu
(
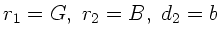 ):
):
Die Determinante dieser Systemmatrix ist aber gleich 1, was man
durch Einsetzen der Matrixelemente prüfen kann. Durch Mischen der
obigen Formeln kann man vier verschiedene Formeln für den
Abbildungsmaßtab herleiten:
Aus den ersten beiden Formeln erhalten wir noch die Newtonsche Form der
Abbildungsgleichung:
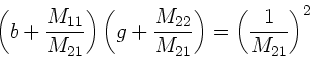 |
(5) |
Optische Systeme mit zwei Linsen (Mikroskop, Fernrohr, Projektor u.s.w)
unterscheiden sich im wesentlichen durch die Brechkräfte
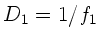 ,
, 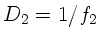 und den Abstand
und den Abstand
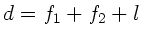 . Beim Mikroskop ist
. Beim Mikroskop ist 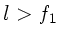 und
und 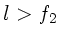 ,
beim Fernrohr
,
beim Fernrohr 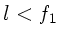 ,
, 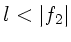 .
Mit diesen Bezeichnungen erhalten wir für die Systemmatrix:
.
Mit diesen Bezeichnungen erhalten wir für die Systemmatrix:
Die Newtonsche Abbildungsgleichung wird hiermit zu
![\begin{displaymath}
\left[ g - \frac{f_{1}(f_{1}+l)}{l} \right] \left[
b - \f...
...2}+l)}{l} \right] = \left( \frac{f_{1}f_{2}}
{l} \right)^{2}
\end{displaymath}](img83.gif) |
(6) |
und der Abbildungsmaßstab zu
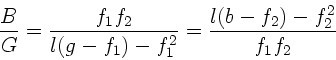 |
(7) |
In der obigen Abbildungsgleichung sind 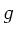 und
und 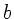 grundsätzlich
Gegenstands- und Bildweite von den Linsenbegrenzungen aus gemessen.
In der älteren Literatur und für zeichnerische Zwecke werden
häufig noch die Hauptebenen eingeführt (siehe Vorlesung). Hierbei
wird dann
grundsätzlich
Gegenstands- und Bildweite von den Linsenbegrenzungen aus gemessen.
In der älteren Literatur und für zeichnerische Zwecke werden
häufig noch die Hauptebenen eingeführt (siehe Vorlesung). Hierbei
wird dann 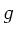 und
und 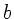 als Abstände von den Hauptebenen definiert.
In der Matrizen-Optik ist die Definition der Hauptebenen
jedoch im allgemeinen überflüssig.
als Abstände von den Hauptebenen definiert.
In der Matrizen-Optik ist die Definition der Hauptebenen
jedoch im allgemeinen überflüssig.
- Aufgabe 4:
Beweisen Sie die beiden letzten Formeln für die Abbildungsgleichung
und den Abbildungsmaßstab.
- Aufgabe 5:
Zwei Sammellinsen mit den Brennweiten 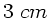 und
und 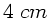 sind auf
einer optischen Bank im Abstand von
sind auf
einer optischen Bank im Abstand von 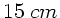 angebracht. Berechnen
Sie, in welchem Abstand vor der ersten, als Objektiv wirkenden Linse
man einen Gegenstand aufstellen muß, damit das System vom Gegenstand
ein virtuelles Bild entwirft, daß sich in der deutlichen Sehweite
befindet. Das Auge des Beobachters sei dicht an die zweite, als
Okular wirkende Linse gerückt.
angebracht. Berechnen
Sie, in welchem Abstand vor der ersten, als Objektiv wirkenden Linse
man einen Gegenstand aufstellen muß, damit das System vom Gegenstand
ein virtuelles Bild entwirft, daß sich in der deutlichen Sehweite
befindet. Das Auge des Beobachters sei dicht an die zweite, als
Okular wirkende Linse gerückt.
Lösungen zu den Rechenübungen am 9.12.92.
Aufgabe 1:
Die Systemmatrix einer Einzellinse ist:
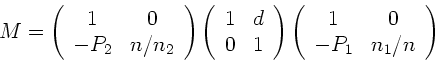 |
(8) |
wobei die Brechkräfte der Flächen durch
gegeben sind. Der Lichtstrahl läuft vom Medium 1 durch die Linse in
das Medium 2. Mit 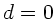 (dünne Linse) folgt:
(dünne Linse) folgt:
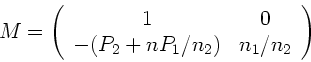 |
(9) |
Daraus folgt:
![\begin{displaymath}
D_{21} = P_{2} + \frac{n}{n_{2}} P_{1} =
\frac{1}{n_{2}} \left[ \frac{n-n_{1}}{R_{a}} - \frac{n-n_{2}}{R_{b}}
\right]
\end{displaymath}](img91.gif) |
(10) |
Aufgabe 2:
Antwort:
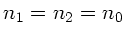 , denn dann gilt:
, denn dann gilt:
Falls der Lichtstrahl von der entgegengesetzten Seite kommt,
ändert sich die Reihenfolge der Flächen und die
Vorzeichen der Krümmungsradien. Daher
![\begin{displaymath}
D_{12} = \frac{n-n_{0}}{n_{0}} \left[ \frac{1}{R_{b}'} -
...
...}} \left[
\frac{1}{R_{a}} - \frac{1}{R_{b}} \right] = D_{21}
\end{displaymath}](img93.gif) |
(11) |
Aufgabe 3:
a) Wir betrachten das System als aus 2 Linsen zusammengesetzt,
zunächst mit Abstand 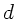 .
.
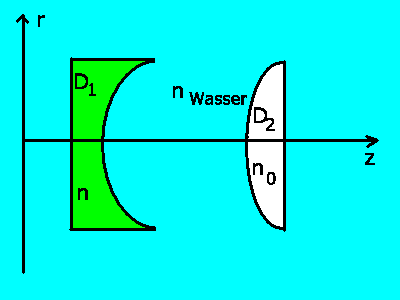
Dann sind die Brechkräfte
Mit 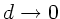 folgt:
folgt:
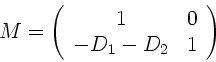 |
(12) |
Daher
b) Der Strahlengang bei einem System dreier brechender Flächen ist
im folgenden gezeigt:
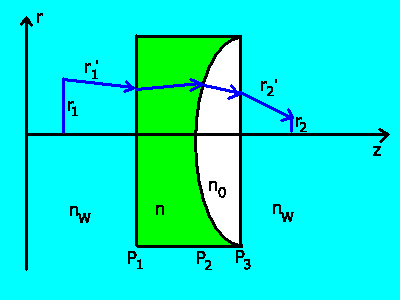
Die Systemmatrix wird zu:
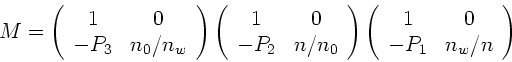 |
(13) |
Wegen
folgt
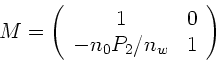 |
(14) |
Daher erhalten wir ebenfalls:
Aufgabe 5:
In der folgenden Abbildung ist 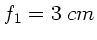 ,
, 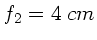 ,
,
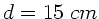 ,
,
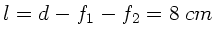 und
und 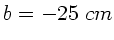 (deutliche
Sehweite):
(deutliche
Sehweite):
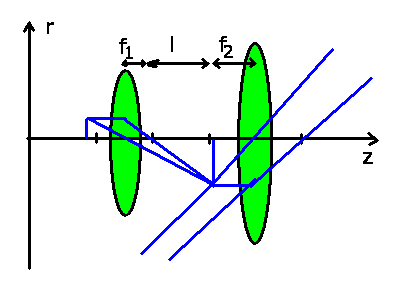
Diese Werte setzen wir in die Abbildungsgleichung
ein und erhalten:
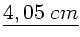 .
.
Harm Fesefeldt
2007-08-22
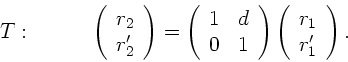
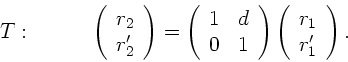

![]() zur optischen
Achse konstant (
zur optischen
Achse konstant (![]() ) und ändert nur die Richtung
) und ändert nur die Richtung
![]() nach
nach ![]() :
:
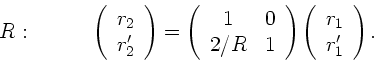


![]() und
und ![]() läßt den Abstand zur
optischen Achse ebenfalls konstant, ändert aber die Richtung des
Lichtstrahls. Der Strahl läuft von Medium 1 nach Medium 2:
läßt den Abstand zur
optischen Achse ebenfalls konstant, ändert aber die Richtung des
Lichtstrahls. Der Strahl läuft von Medium 1 nach Medium 2:

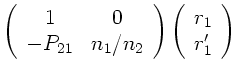
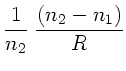

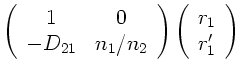
![$\displaystyle \frac{1}{n_{2}} \left[ \frac{n-n_{1}}{R_{1}} -
\frac{n-n_{2}}{R_{2}} \right]$](img23.gif)

![]() ist positiv, wenn die Krümmung von der Richtung des
Lichtstrahls
aus gesehen konvex ist,
ist positiv, wenn die Krümmung von der Richtung des
Lichtstrahls
aus gesehen konvex ist, ![]() ist negativ,
wenn die Krümmung von der
Richtung des Lichtstrahls aus gesehen konkav ist.
ist negativ,
wenn die Krümmung von der
Richtung des Lichtstrahls aus gesehen konkav ist. 


![]() bereits
bei der Aufstellung der Transformationen einzusetzen, sodaß in den
Rechnungen selbst
bereits
bei der Aufstellung der Transformationen einzusetzen, sodaß in den
Rechnungen selbst ![]() stets positiv ist.
Schließlich sollte noch erwähnt werden, daß die Transformationen
der Brechung und Reflexion auch für den Grenzfall
stets positiv ist.
Schließlich sollte noch erwähnt werden, daß die Transformationen
der Brechung und Reflexion auch für den Grenzfall ![]() gelten, d.h. auch für ebene Begrenzungsflächen gültig sind.
gelten, d.h. auch für ebene Begrenzungsflächen gültig sind. 
![]() (d.h.
(d.h.
![]() in der
Linsenmatrix),
das Linsenmaterial sei immer Glas mit Brechungsindex
in der
Linsenmatrix),
das Linsenmaterial sei immer Glas mit Brechungsindex ![]() .
Dann erhalten wir für die Brechkräfte der Linsen:
.
Dann erhalten wir für die Brechkräfte der Linsen:
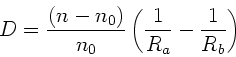


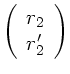
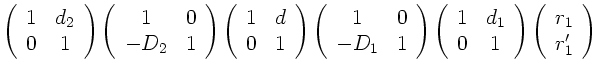
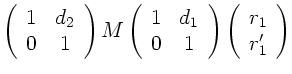

![]() läßt sich leicht auswerten und ergibt:
läßt sich leicht auswerten und ergibt:
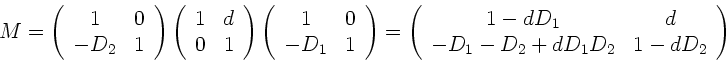

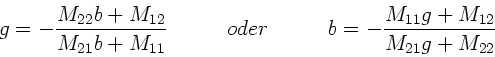
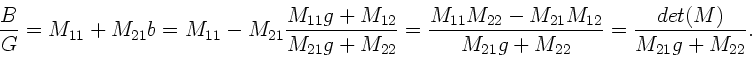
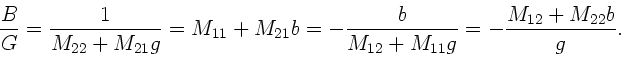
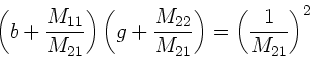
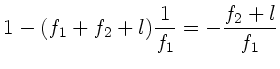
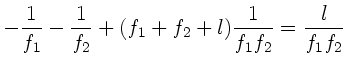
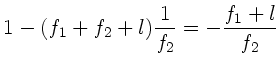
![\begin{displaymath}
\left[ g - \frac{f_{1}(f_{1}+l)}{l} \right] \left[
b - \f...
...2}+l)}{l} \right] = \left( \frac{f_{1}f_{2}}
{l} \right)^{2}
\end{displaymath}](img83.gif)
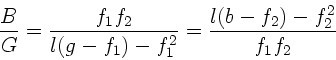
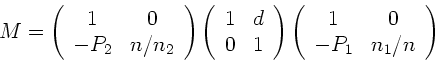

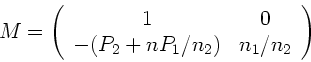
![\begin{displaymath}
D_{21} = P_{2} + \frac{n}{n_{2}} P_{1} =
\frac{1}{n_{2}} \left[ \frac{n-n_{1}}{R_{a}} - \frac{n-n_{2}}{R_{b}}
\right]
\end{displaymath}](img91.gif)
![\begin{displaymath}
D_{21} = \frac{1}{n_{0}} \left[ \frac{n-n_{0}}{R_{a}} -
\frac{n-n_{0}}{R_{b}} \right]
\end{displaymath}](img92.gif)
![\begin{displaymath}
D_{12} = \frac{n-n_{0}}{n_{0}} \left[ \frac{1}{R_{b}'} -
...
...}} \left[
\frac{1}{R_{a}} - \frac{1}{R_{b}} \right] = D_{21}
\end{displaymath}](img93.gif)

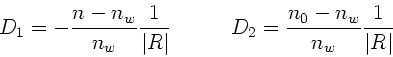
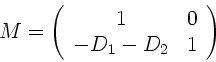
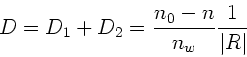

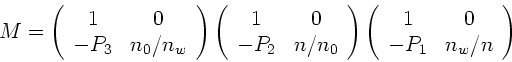
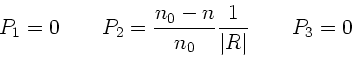
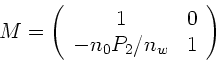
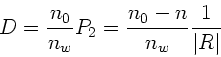

![\begin{displaymath}
\left[ g- \frac{f_{1}(f_{2}+l)}{l} \right] \left[ b -
\fra...
..._{2}+l)}{l} \right] = \left( \frac{f_{1}f_{2}}{l} \right)^{2}
\end{displaymath}](img107.gif)