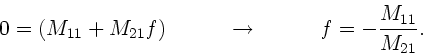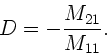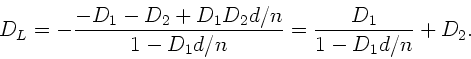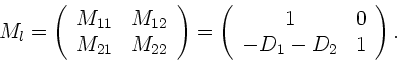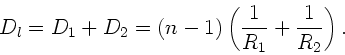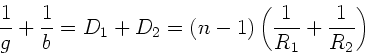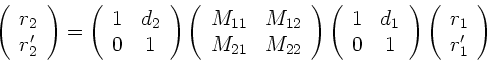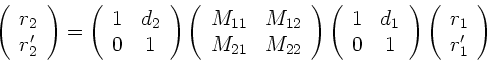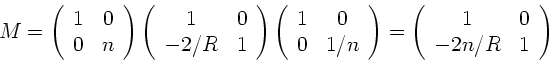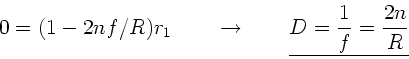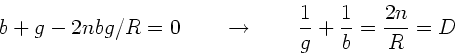Physik III, WS 1992/93
Rechenübungen am 2. Dezember 1992
Grundlagen der paraxialen Matrizen- Optik
In der Vorlesung werden die Formeln für Reflexion und Brechung
an geraden und gekrümmten Flächen diskutiert. Es zeigt sich dabei,
daß es ausgesprochen mühsam und unübersichtlich ist, mit Hilfe
dieser Formeln die Abbildungsgesetze für kompliziertere optische
Systeme herzuleiten und zu diskutieren. In dieser Übung wollen wir
ein mathematisches Verfahren kennenlernen, mit dessen Hilfe man in
einfacher Weise die kompliziertesten optischen Systeme studieren
kann. Dieses Verfahren eignet sich insbesondere für Anwendungen
auf Rechenanlagen und ist daher gerade in den letzten Jahrzehnten
außerordentlich gut ausgearbeitet worden. Wir beschränken uns
hier auf die paraxiale Optik, d.h. wir betrachten nur Lichtstrahlen,
die nahe zur optischen Achse verlaufen und deren Winkel mit der
optischen Achse klein sind. Wir wählen die 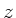 - Achse als optische
Achse und bezeichnen mit
- Achse als optische
Achse und bezeichnen mit 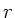 den Abstand eines Punktes von der
den Abstand eines Punktes von der
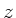 - Achse. In der paraxialen Optik verlaufen alle Lichtstrahlen
in einer Ebene durch die optische Achse. Der Abstand
- Achse. In der paraxialen Optik verlaufen alle Lichtstrahlen
in einer Ebene durch die optische Achse. Der Abstand 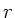 liege genau
in dieser Ebene. Wir definieren einen zweidimensionalen Vektor
liege genau
in dieser Ebene. Wir definieren einen zweidimensionalen Vektor 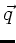 ,
dessen Komponenten einmal der Abstand
,
dessen Komponenten einmal der Abstand 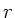 , und zum anderen
die Richtung
, und zum anderen
die Richtung 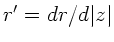 bezüglich der optischen Achse sind, d.h.
bezüglich der optischen Achse sind, d.h.
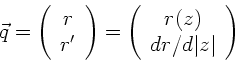 |
(1) |
In der paraxialen Optik gilt die Näherung
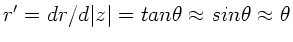 , wobei
, wobei
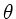 der Winkel des Lichtstrahls mit der optischen Achse ist.
Die geradliniege Bewegung eines Lichtstrahls
der Winkel des Lichtstrahls mit der optischen Achse ist.
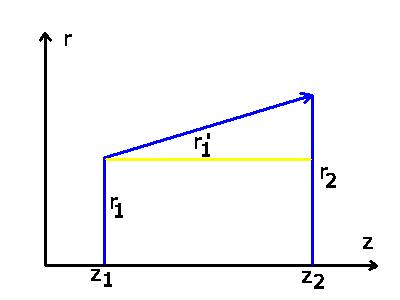
Die geradliniege Bewegung eines Lichtstrahls
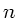 von Punkt
von Punkt 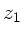 bis zum Punkt
bis zum Punkt 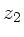 läßt sich darstellen durch
die Transformation (siehe Abbildung oben):
läßt sich darstellen durch
die Transformation (siehe Abbildung oben):
wobei
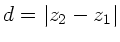 die Länge der Strecke ist.
Eine Translation ändert natürlich nicht die Steigung, bzw den
Winkel des Lichtstrahls mit der optischen Achse, sondern nur den
Abstand
die Länge der Strecke ist.
Eine Translation ändert natürlich nicht die Steigung, bzw den
Winkel des Lichtstrahls mit der optischen Achse, sondern nur den
Abstand 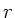 . Diese Translation kann auch mit Hilfe einer Matrizen-
Gleichung in der folgenden Form geschrieben werden:
. Diese Translation kann auch mit Hilfe einer Matrizen-
Gleichung in der folgenden Form geschrieben werden:
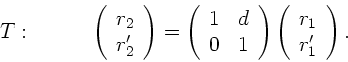 |
(2) |
Die Matrix selbst nennt man die
Translationsmatrix 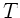 oder auch
oder auch 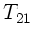 , um anzudeuten, daß eine
Transformation vom Punkt
, um anzudeuten, daß eine
Transformation vom Punkt 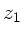 zum Punkt
zum Punkt 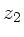 durchzuführen ist.
durchzuführen ist.
Als nächstes diskutieren wir die Reflexion eines Lichtstrahls an einer
sphärischen Begrenzung. Hierbei ändert sich nicht der Abstand zur
optischen Achse, sondern nur die Richtung bzw der Winkel des Strahls
mit der optischen Achse. In Matrizen- Schreibweise gilt dann:
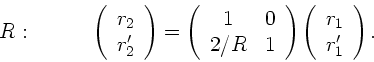 |
(3) |
Der Krümmungsradius 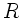 kann hierbei positiv oder negativ
sein, je nachdem ob die gekrümmte Fläche dem Lichtstrahl
konvex oder konkav erscheint.
(siehe nachstehende Skizze). Die Matrix
kann hierbei positiv oder negativ
sein, je nachdem ob die gekrümmte Fläche dem Lichtstrahl
konvex oder konkav erscheint.
(siehe nachstehende Skizze). Die Matrix 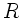 ist die Reflexionsmatrix.
Man schreibt hierfür auch
ist die Reflexionsmatrix.
Man schreibt hierfür auch 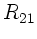 , um anzudeuten, daß eine
Reflexion an der Trennfläche von Medium 1 und Medium 2 stattgefunden
hat.
, um anzudeuten, daß eine
Reflexion an der Trennfläche von Medium 1 und Medium 2 stattgefunden
hat.
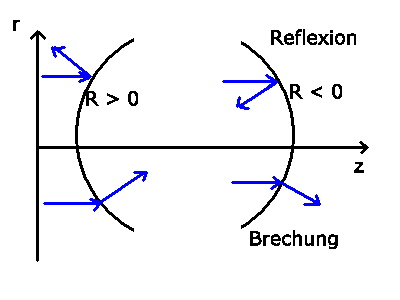
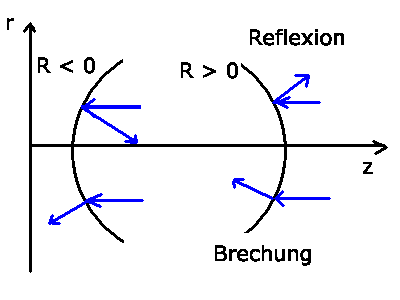
Als letzte Transformation benötigen wir noch die Brechung an
Begrenzungsflächen zwischen zwei Medien. Diese ist gegeben durch
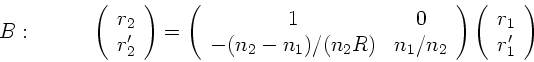 |
(4) |
Die Vorzeichenkonvention für
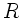 ist die gleiche wie bei der Reflexion.
ist die gleiche wie bei der Reflexion.
Die hier definierte Vorzeichenkonvention ist leider nicht
eindeutig in verschiedenen literarischen Darstellungen der Matrizen- Optik.
Wir widerholen daher unsere Vorzeichenkonvention
noch einmal:
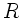 ist positiv, wenn die Krümmung von der Richtung des
Lichtstrahls
aus gesehen konvex ist,
ist positiv, wenn die Krümmung von der Richtung des
Lichtstrahls
aus gesehen konvex ist, 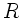 ist negativ,
wenn die Krümmung von der
Richtung des Lichtstrahls aus gesehen konkav ist.
Im übrigen ist es empfehlenswert, die Vorzeichen von
ist negativ,
wenn die Krümmung von der
Richtung des Lichtstrahls aus gesehen konkav ist.
Im übrigen ist es empfehlenswert, die Vorzeichen von 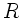 bereits
bei der Aufstellung der Transformationen einzusetzen, sodaß in den
Rechnungen selbst
bereits
bei der Aufstellung der Transformationen einzusetzen, sodaß in den
Rechnungen selbst 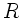 stets positiv ist.
stets positiv ist.
Schließlich sollte noch erwähnt werden, daß die Transformationen
der Brechung und Reflexion auch für den Grenzfall 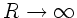 gelten, d.h. auch für ebene Begrenzungsflächen gültig sind.
gelten, d.h. auch für ebene Begrenzungsflächen gültig sind.
Durch Mehrfachanwendung kann man mit Hilfe dieser drei Transformationen
beliebig komplizierte Systeme zusammensetzen.
Wir demonstrieren das
Verfahren an einigen einfachen Beispielen.
Beispiel 1: Das erste Beispiel soll noch einmal zeigen, daß das Brechungsgesetz
durch diese Transformationen richtig beschrieben wird.
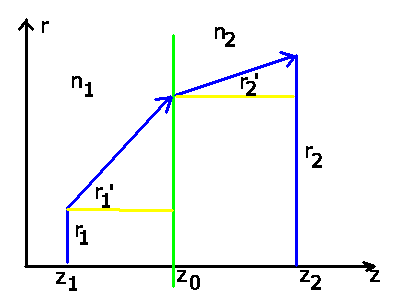
Die Transformation besteht aus 3 Schritten. Zunächst führen wir
eine Translation vom Punkt 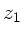 zum Punkt
zum Punkt 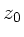 , der
, der 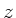 -
Koordinate der Begrenzungsfläche. Schließlich führt eine weitere
Translation zum Punkt
-
Koordinate der Begrenzungsfläche. Schließlich führt eine weitere
Translation zum Punkt 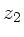 . Man beachte, daß bei der Brechung
in diesem Fall
. Man beachte, daß bei der Brechung
in diesem Fall
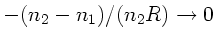 , da
, da 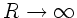 .
.
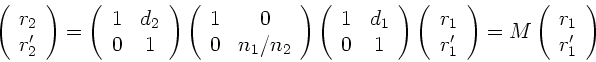 |
(5) |
wobei
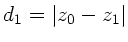 und
und
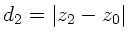 . Ausmultiplizieren der Matrizen führt dann auf:
. Ausmultiplizieren der Matrizen führt dann auf:
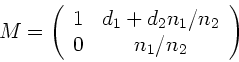 |
(6) |
Die Transformation lautet ausgeschrieben:
Da
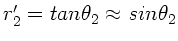 und
und
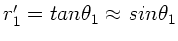 , folgt aus der
zweiten Gleichung
, folgt aus der
zweiten Gleichung
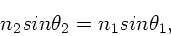 |
(9) |
also das uns bekannte Brechungsgesetz.
Aufgabe 1:
Zeigen Sie die Gültigkeit des Reflexionsgesetzes an einer ebenen
Begrenzungsfläche mit Hilfe der paraxialen Matrizen- Optik.
Beispiel 2:
Unser zweites Beispiel behandelt die Reflexion an einer sphärischen
Kugelfläche.
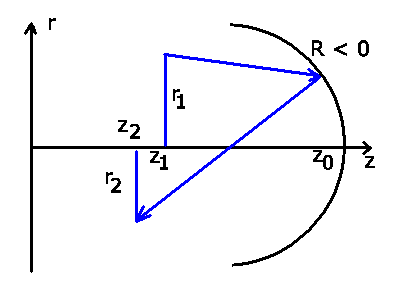
Wir setzen
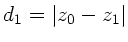 und
und
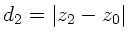 .
Die Transformation lautet (man beachte
.
Die Transformation lautet (man beachte 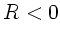 , da Begrenzung konkav):
, da Begrenzung konkav):
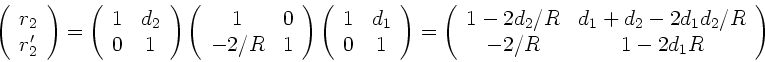 |
(10) |
Die Transformation lautet also ausgeschrieben:
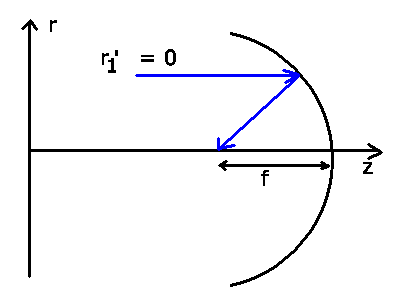
Zur Berechnung des Brennpunkts nehmen wir Strahlen, die parallel
zur optischen Achse laufen (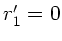 ) und berechnen die Strecke
) und berechnen die Strecke
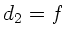 , bei der diese Strahlen nach der Reflektion die optische
Achse schneiden (
, bei der diese Strahlen nach der Reflektion die optische
Achse schneiden (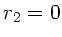 ). Dieses ergibt:
). Dieses ergibt:
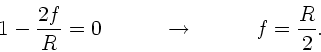 |
(13) |
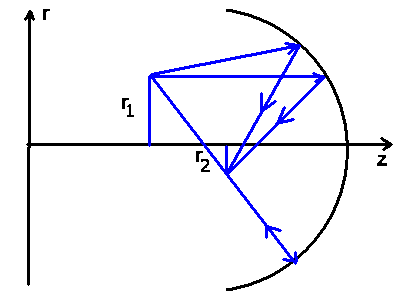
Die Abbildungsgleichung erhält man ebenso einfach (siehe Skizze
oben rechts). Falls 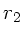 das Bild von
das Bild von 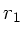 ist, so müssen
sich alle von
ist, so müssen
sich alle von 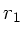 ausgehenden Strahlen in
ausgehenden Strahlen in 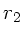 schneiden,
unabhängig von der Steigung
schneiden,
unabhängig von der Steigung 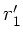 . Daher muß der Koeffizient
von
. Daher muß der Koeffizient
von 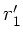 in der ersten der beiden Transformationsformeln
verschwinden. In diesem Fall ist aber
in der ersten der beiden Transformationsformeln
verschwinden. In diesem Fall ist aber 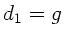 und
und 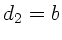 :
:
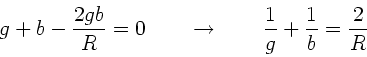 |
(14) |
Aufgabe 2:
Ein Kugelsegment aus Glas sei auf der gekrümmten Fläche versilbert.
Der Radius der Kugel ist 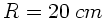 und das Glas habe den
Brechungsindex
und das Glas habe den
Brechungsindex 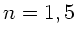 . Die Dicke
. Die Dicke 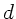 des Segmentes sei
vernachlässigbar, d.h.
des Segmentes sei
vernachlässigbar, d.h. 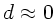 .
.
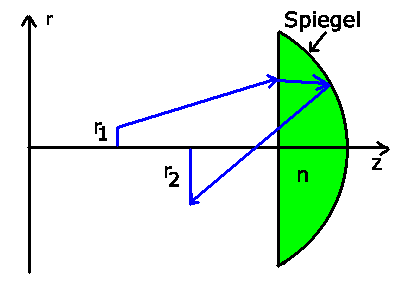
a) Berechnen Sie die Brechkraft für paraxiale Lichtstrahlen, die
durch die ebene Fläche in das Glas eintreten, an der gekrümmten
Spiegelfläche reflektiert werden und wieder aus dem Glas
austreten.
b) Ein Bild sei bei der Gegenstandsweite 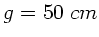 senkrecht zur
optischen Achse angeordnet. Wo liegt das Bild auf der optischen Achse ?
senkrecht zur
optischen Achse angeordnet. Wo liegt das Bild auf der optischen Achse ?
Beispiel 3:
Als drittes Beispiel diskutieren wir die Abbildung mit einer Linse.
Die Transformationen sind in der folgenden Abbildung skizziert.
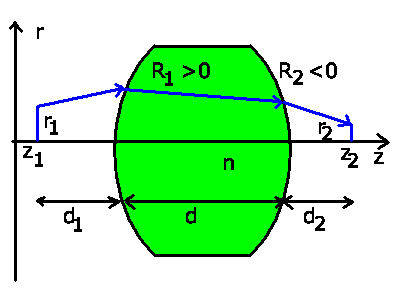
Zunächst eine Translation bis zur ersten brechenden Fläche,
nach der Brechung eine zweite Translation durch die Linse, eine
weitere Brechung an der zweiten Begrenzungsfläche der Linse, sowie
schließlich eine Transformation zum Punkt 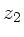 . Das Linsenmaterial
habe den Brechungsindex
. Das Linsenmaterial
habe den Brechungsindex 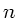 , die Umgebung sei Luft mit dem
Brechungsindex
, die Umgebung sei Luft mit dem
Brechungsindex 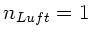 . Die Abstände seien
. Die Abstände seien
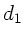 ,
, 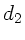 sowie die Dicke der Linse
sowie die Dicke der Linse 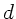 .
Die Krümmungsradien seien
.
Die Krümmungsradien seien 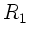 und
und 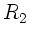 .
Man beachte aber, daß bei der linken konvexen
Fläche
.
Man beachte aber, daß bei der linken konvexen
Fläche 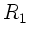 positiv, bei der rechten konkaven Fläche
positiv, bei der rechten konkaven Fläche
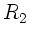 negativ ist.
Dann erhalten wir die Transformation
negativ ist.
Dann erhalten wir die Transformation
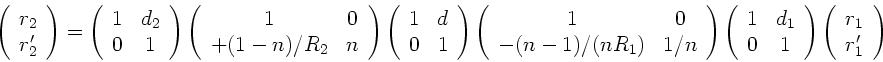 |
(15) |
Wir wiederholen nochmal, daß wir die Vorzeichen von 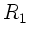 und
und
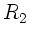 bei der Aufstellung der Transformation bereits angbracht haben,
in der weiteren Rechnung sind
bei der Aufstellung der Transformation bereits angbracht haben,
in der weiteren Rechnung sind 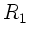 und
und 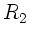 also beide positiv.
Die mittleren drei Matrizen beschreiben das Verhalten der Linse, die beiden
äußeren Matrizen bilden die Translationen zur vorderen Linsenbegrenzung
bzw von der hinteren Linsenbegrenzung zum Endpunkt
also beide positiv.
Die mittleren drei Matrizen beschreiben das Verhalten der Linse, die beiden
äußeren Matrizen bilden die Translationen zur vorderen Linsenbegrenzung
bzw von der hinteren Linsenbegrenzung zum Endpunkt 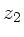 .
Wir schreiben die Gesamtmatrix daher in der Form
.
Wir schreiben die Gesamtmatrix daher in der Form
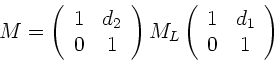 |
(16) |
wobei 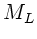 also die Linsenmatrix ist. Mit der Abkürzung
also die Linsenmatrix ist. Mit der Abkürzung
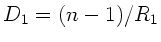 und
und
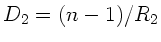 ist die Linsenmatrix:
ist die Linsenmatrix:
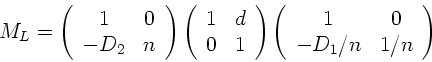 |
(17) |
Hierfür ergibt sich nach kurzer Rechnung:
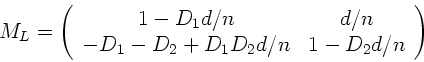 |
(18) |
Wir setzen im folgenden die Elemente der Linsenmatrix gleich
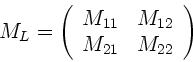 |
(19) |
also ausgeschrieben:
Wir müssen noch die Transformationen von den Begrenzungsflächen
zu den Punkten 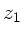 und
und 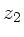 durchführen, d.h.
durchführen, d.h.
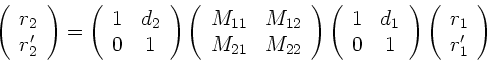 |
(24) |
Die Lösung ist einfach und ergibt
Im folgenden wollen wir noch zwei wichtige Folgerungen herausarbeiten.
Falls die Strahlen parallel zur optischen Achse in die Linse
eintreten, so werden sie nach Definition in den Brennpunkt
abgebildet.
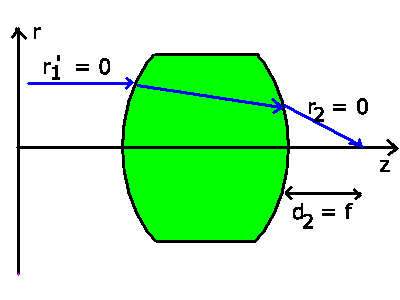
Für parallel einfallende Strahlen gilt aber 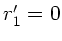 . Außerdem
muß
. Außerdem
muß 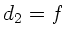 sein, sofern wir
sein, sofern wir 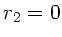 setzen, d.h.
setzen, d.h.
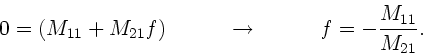 |
(27) |
Für die Brechkraft gilt entsprechend (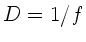 ):
):
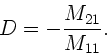 |
(28) |
Setzen wir die Ausdrücke der Matrizelemente ein, so folgt für die
allgemeine Linse:
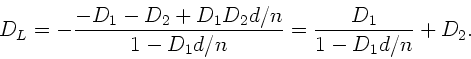 |
(29) |
Auch die Abbildungsgleichung kann sehr einfach hergeleitet werden.
Wir setzen 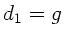 ,
, 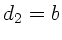 und erhalten
und erhalten
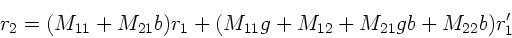 |
(30) |
Alle von 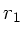 ausgehenden Strahlen müssen sich in
ausgehenden Strahlen müssen sich in 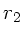 schneiden,
und zwar unabhängig von der Steigung
schneiden,
und zwar unabhängig von der Steigung 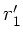 . Daher muß der
Koeffizient von
. Daher muß der
Koeffizient von 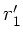 verschwinden:
verschwinden:
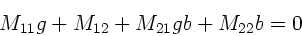 |
(31) |
Approximation für dünne Linsen.
Wir wollen zum Schluß die Brechkraft und die Abbildungsgleichung
für den Spezialfall der dünnen Linse noch einmal
hinschreiben. Bei der dünnen Linse wird die Approximation
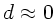 gemacht. Dann wird die Linsenmatrix extrem einfach,
gemacht. Dann wird die Linsenmatrix extrem einfach,
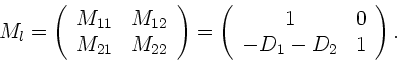 |
(32) |
Die Brechkraft errechnet sich zu
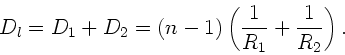 |
(33) |
Für die Abbildungsgleichung erhalten wir:
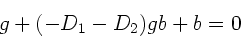 |
(34) |
Mit der Umformung
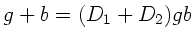 folgt sofort:
folgt sofort:
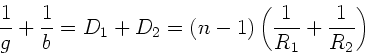 |
(35) |
Lösungen zu den Rechenübungen am 2. Dezember 1992.
Aufgabe 1:
Transformationsgleichung:
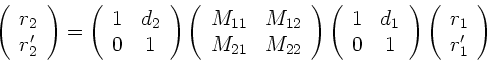 |
(36) |
Lösung:
Aufgabe 2:
Die allgemeine Transformation besteht aus 7 Matrizen, von denen wir
die Translation durch das Linsenmaterial aber sofort vernachlässigen
können, da in diesen Schritten (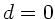 ) die Translationsmatrizen zu
Einheitsmatrizen werden. Es bleibt
) die Translationsmatrizen zu
Einheitsmatrizen werden. Es bleibt
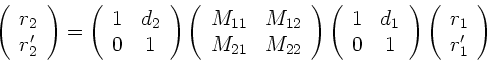 |
(39) |
mit
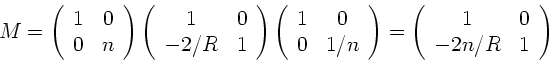 |
(40) |
Die Transformationen lauten also:
a) Achsenparallele Strahlen (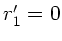 ) schneiden (
) schneiden (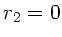 )
die optische Achse bei
)
die optische Achse bei
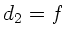 . Daher folgt aus der ersten Gleichung:
. Daher folgt aus der ersten Gleichung:
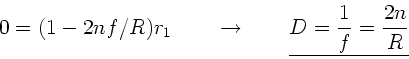 |
(43) |
b) Wenn 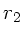 das Bild von
das Bild von 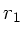 sein soll, so müssen alle
von
sein soll, so müssen alle
von 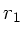 ausgehenden Strahlen sich in
ausgehenden Strahlen sich in 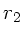 schneiden,
unabhängig von
schneiden,
unabhängig von 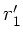 . Daher muß der Koeffizient von
. Daher muß der Koeffizient von 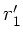 in der ersten Transformationsgleichung verschwinden. Für
in der ersten Transformationsgleichung verschwinden. Für 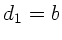 und
und 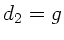 gilt also:
gilt also:
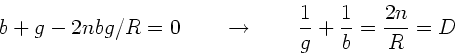 |
(44) |
Zahlenwerte:
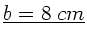
Harm Fesefeldt
2007-08-22
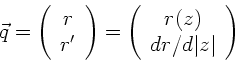
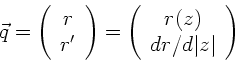

![]() , wobei
, wobei
![]() der Winkel des Lichtstrahls mit der optischen Achse ist.
Die geradliniege Bewegung eines Lichtstrahls
der Winkel des Lichtstrahls mit der optischen Achse ist.
Die geradliniege Bewegung eines Lichtstrahls
![]() von Punkt
von Punkt ![]() bis zum Punkt
bis zum Punkt ![]() läßt sich darstellen durch
die Transformation (siehe Abbildung oben):
läßt sich darstellen durch
die Transformation (siehe Abbildung oben):
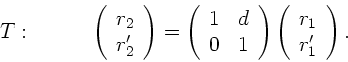
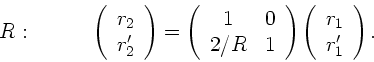


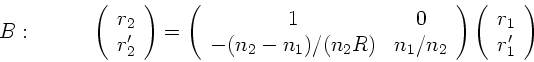

![]() zum Punkt
zum Punkt ![]() , der
, der ![]() -
Koordinate der Begrenzungsfläche. Schließlich führt eine weitere
Translation zum Punkt
-
Koordinate der Begrenzungsfläche. Schließlich führt eine weitere
Translation zum Punkt ![]() . Man beachte, daß bei der Brechung
in diesem Fall
. Man beachte, daß bei der Brechung
in diesem Fall
![]() , da
, da ![]() .
.
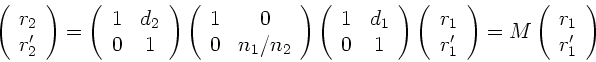
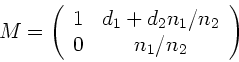
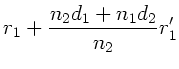

![]() und
und
![]() .
Die Transformation lautet (man beachte
.
Die Transformation lautet (man beachte ![]() , da Begrenzung konkav):
, da Begrenzung konkav):
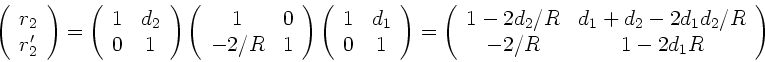
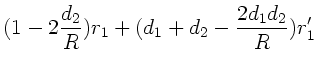
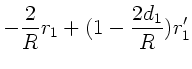


![]() ) und berechnen die Strecke
) und berechnen die Strecke
![]() , bei der diese Strahlen nach der Reflektion die optische
Achse schneiden (
, bei der diese Strahlen nach der Reflektion die optische
Achse schneiden (![]() ). Dieses ergibt:
). Dieses ergibt:
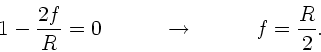
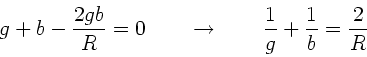

![]() senkrecht zur
optischen Achse angeordnet. Wo liegt das Bild auf der optischen Achse ?
senkrecht zur
optischen Achse angeordnet. Wo liegt das Bild auf der optischen Achse ?

![]() . Das Linsenmaterial
habe den Brechungsindex
. Das Linsenmaterial
habe den Brechungsindex ![]() , die Umgebung sei Luft mit dem
Brechungsindex
, die Umgebung sei Luft mit dem
Brechungsindex ![]() . Die Abstände seien
. Die Abstände seien
![]() ,
, ![]() sowie die Dicke der Linse
sowie die Dicke der Linse ![]() .
Die Krümmungsradien seien
.
Die Krümmungsradien seien ![]() und
und ![]() .
Man beachte aber, daß bei der linken konvexen
Fläche
.
Man beachte aber, daß bei der linken konvexen
Fläche ![]() positiv, bei der rechten konkaven Fläche
positiv, bei der rechten konkaven Fläche
![]() negativ ist.
Dann erhalten wir die Transformation
negativ ist.
Dann erhalten wir die Transformation
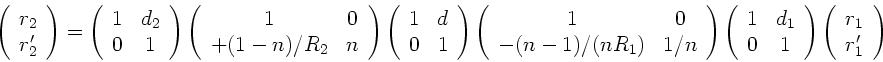
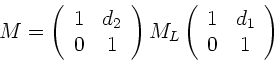
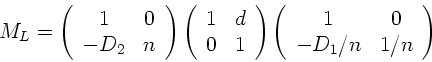
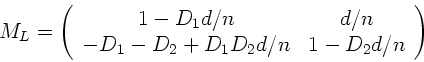
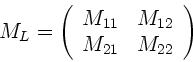
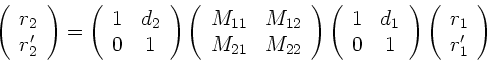

![]() . Außerdem
muß
. Außerdem
muß ![]() sein, sofern wir
sein, sofern wir ![]() setzen, d.h.
setzen, d.h.