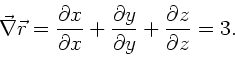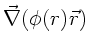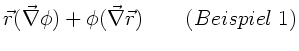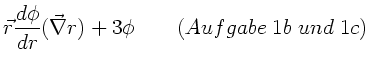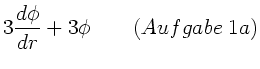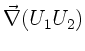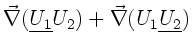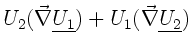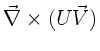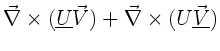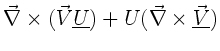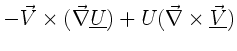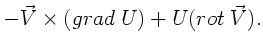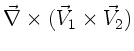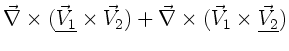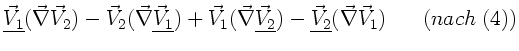Physik III, WS 1992/93
Rechenübungen am 11. November 1992
Ergänzungen zur Vektoranalysis
In der Elektrodynamik sowie insbesondere bei der Behandlung der
Maxwell- Gleichungen wird vielfach von Vektoroperatoren Gebrauch
gemacht.
Für die Differentialoperatoren gilt in kartesischen Koordinaten:
Hier und in allen weiteren Formeln bezeichnen wir mit 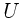 ein
Skalarfeld und mit
ein
Skalarfeld und mit 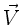 ein Vektorfeld. Man kann leicht zeigen,
daß der Gradient, die Divergenz und die Rotation einer Summe von
Feldern additiv auf die Felder angewendet werden können:
ein Vektorfeld. Man kann leicht zeigen,
daß der Gradient, die Divergenz und die Rotation einer Summe von
Feldern additiv auf die Felder angewendet werden können:
Ebenso gilt natürlich, wenn 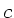 ein konstanter Skalar ist,
ein konstanter Skalar ist,
Einzig die Regeln zur Anwendung von Differentialoperatoren auf
Produkte von skalaren und vekoriellen Feldern sind etwas komplizierter.
Wie wollen diese Regeln hier nicht beweisen, sondern ein
Kochrezept
diskutieren, nach dem alle Regeln relativ einfach hergeleitet werden
können. Wir schreiben das Produkt einer beliebigen Anzahl von
skalaren und vektoriellen Felder in der Form
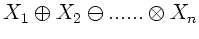 . Die Symbole
. Die Symbole
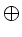 ,
, 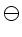 und
und 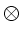 bezeichnen hierbei eine
skalare oder vektorielle Multiplikation. Wir schreiben dann
bezeichnen hierbei eine
skalare oder vektorielle Multiplikation. Wir schreiben dann
Dieses soll andeuten, daß wir den Nablaoperator auf die mit dem
Unterstrich versehene Funktion anwenden müssen und anschließend
alle Summanden addieren. Danach werden die so gewonnenen Produkte
nach den Regeln der Vektoralgebra so umgeformt, daß nach dem
Nablaoperator  nur noch die mit dem Unterstrich versehene
Funktion steht. Beim letzten Schritt wird der Nablaoperator wie ein
normaler Vektor behandelt. Die hierzu wichtigsten Regeln der
Vektoralgebra sind:
nur noch die mit dem Unterstrich versehene
Funktion steht. Beim letzten Schritt wird der Nablaoperator wie ein
normaler Vektor behandelt. Die hierzu wichtigsten Regeln der
Vektoralgebra sind:
Formel (3) merkt man sich am besten unter der Rubrik der
zyklischen Vertauschung. Regel (4) ist sicherlich am schwierigsten
zu merken. Weiterhin muß beachtet werden, daß
Falls man diese Regeln der Vektoralgebra weiß,
kann man viele Regeln für die Differentialoperatoren leicht herleiten.
Beispiel 1:
In diesem Beispiel sollte beachtet werden, daß 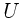 kein Vektor,
sondern ein Skalar ist. Dieser kann also beliebig in den Vektorprodukten
hin- und hergeschoben werden. Daher ist nur Regel (1) zu beachten.
kein Vektor,
sondern ein Skalar ist. Dieser kann also beliebig in den Vektorprodukten
hin- und hergeschoben werden. Daher ist nur Regel (1) zu beachten.
Beispiel 2:
Beispiel 3:
Wegen (4) und (1) gilt
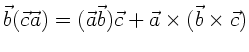 . Identifizieren wir hier
. Identifizieren wir hier
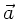 mit
mit 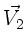 ,
, 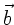 mit
mit  und
und 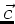 mit
mit 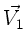 , so folgt
, so folgt
Entsprechend kann der zweite Term umgeformt werden. Insgesamt folgt:
Aufgabe 1:
a) Berechnen Sie 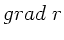 .
.
b) Wie in der normalen Analysis gilt für den Gradienten einer
mittelbaren Funktion:
Berechnen Sie hiermit den Gradienten des Zentralfeldes
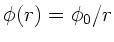 .
.
c) Berechnen Sie
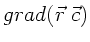 , wobei
, wobei 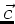 ein
konstanter Vektor ist.
ein
konstanter Vektor ist.
Aufgabe 2:
Berechnen Sie die Divergenz der Zentralfelder
a)
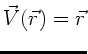
b)
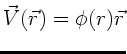
Aufgabe 3:
Berechnen Sie die Ausdrücke für
a)
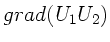
b)
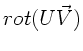
c)
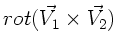
Aufgabe 4:
Der Vektor
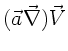 heißt der Gradient des
Vektorfeldes
heißt der Gradient des
Vektorfeldes 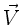 nach dem Vektor
nach dem Vektor 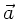 .
Zeigen Sie, daß
.
Zeigen Sie, daß
Aufgabe 5:
Überzeugen Sie sich davon, daß für jedes Feld 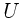 und
und 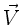 gilt:
gilt:
a)
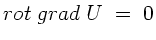
b)
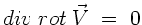 .
.
Lösungen zu den Rechenübungen am 11.November 1992.
Aufgabe 1:
a) Man zeigt explizit, daß
b) Wir setzen 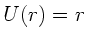 , dann ist
, dann ist
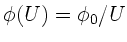 . Damit folgt:
. Damit folgt:
c) Nach Beispiel 3 ist:
Man zeigt explizit, daß
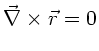 , also
, also
Aufgabe 2:
a) Wir rechnen explizit:
b) Mit den Ergebnissen von Beispiel 1 sowie der Aufgabe 1 folgt
Aufgabe 3:
a)
b)
c)
Nach zwei weiteren, bereits mehrfach durchgeführten Schritten folgt:
Aufgabe 4:
Folgt aus Beispiel 3 und Aufgabe 3c.
Aufgabe 5:
Folgt durch explizites Rechnen aus den Definitionen der Operatoren
Harm Fesefeldt
2007-08-21
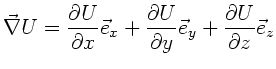
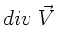
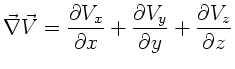
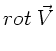
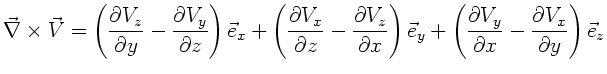
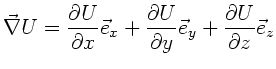
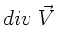
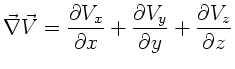
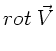
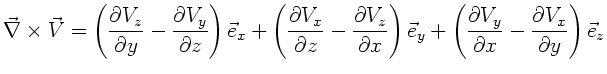
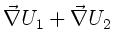
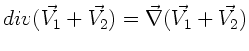
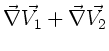
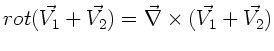
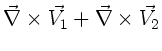
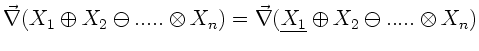
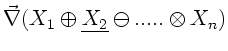
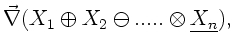
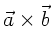
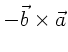
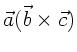
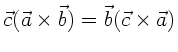
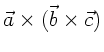
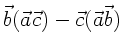
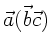
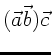
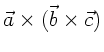
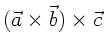
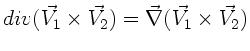
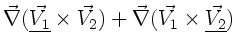
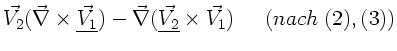
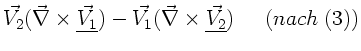
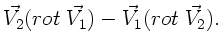
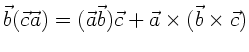 . Identifizieren wir hier
. Identifizieren wir hier
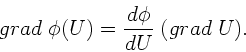
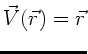
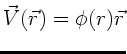
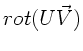
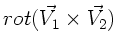
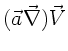 heißt der Gradient des
Vektorfeldes
heißt der Gradient des
Vektorfeldes 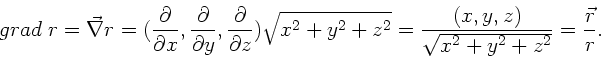
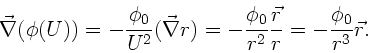
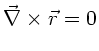 , also
, also