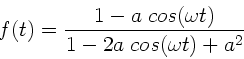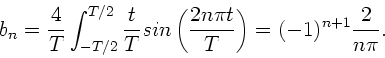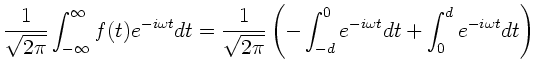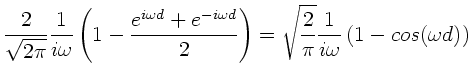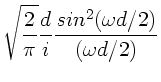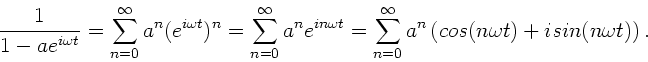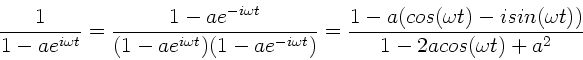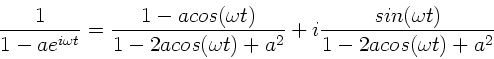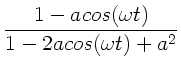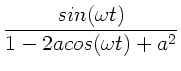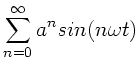Physik III, WS 1992/93
Rechenübungen am 4. November 1992
Ergänzungen zur Fourier- Analyse
Periodische Funktionen 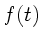 mit der Periode
mit der Periode 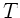 können in eine Fourier-
Reihe entwickelt werden,
können in eine Fourier-
Reihe entwickelt werden,
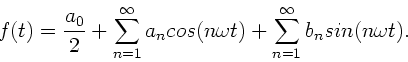 |
(1) |
Die Fourierkoeffizienten 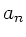 und
und 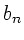 können hierbei in den
folgenden Formen geschrieben werden:
können hierbei in den
folgenden Formen geschrieben werden:
Hieraus und den Symmetrieeigenschaften der Zeitfunktion 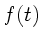 kann
man die verschwindenden Fourier- Koeffizienten bestimmen:
kann
man die verschwindenden Fourier- Koeffizienten bestimmen:
 |
(6) |
Sofern man einen Rechner zur Verfügung hat (hier genügt ein
programmierbarer Taschenrechner), kann man die Integration
numerisch durchführen. Man unterteilt das Integrationsintervall
![$[0,T]$](img14.gif) in
in 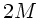 Teilintervalle mit den Stützstellen
Teilintervalle mit den Stützstellen
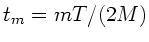 , berechnet an diesen Stützstellen die
Funktionswerte
, berechnet an diesen Stützstellen die
Funktionswerte
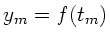 und bildet die Summen
und bildet die Summen
Der zugrunde liegende Algorithmus ist die Trapezformel der numerischen
Integration.
Hierbei muß bemerkt werden, daß man für die verschwindenden
Koeffizienten im allgemeinen keine guten Resultate erhält, d.h.
sie sind relativ weit von Null verschieden.
Außerdem sollte grundsätzlich mit doppelter Genauigkeit (64 bit)
gerechnet werden, was bei Taschenrechnern sowieso der Fall ist.
Komplexe Schreibweise
Die Formeln der Fourier- Analyse lassen sich kompakter schreiben,
wenn man komplexe Zahlen einführt. Wegen
 |
(10) |
folgt bei Einsetzen in die Fourier- Reihe
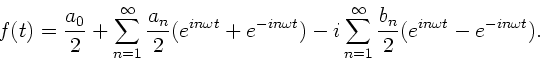 |
(11) |
Wir sortieren nach
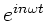 und
und
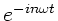 :
:
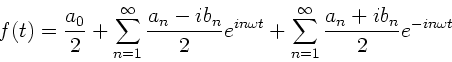 |
(12) |
Mit den Festsetzungen
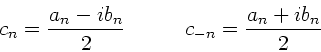 |
(13) |
folgt schließlich
Reihenentwicklungen
Für praktische Anwendungen sind normale Reihenentwicklungen außerordentlich
nützlich. Sei 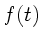 eine reelle Funktion, die als Real- oder
Imaginärteil einer komplexen Funktion
eine reelle Funktion, die als Real- oder
Imaginärteil einer komplexen Funktion 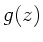 mit
mit
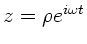 geschrieben werden kann:
geschrieben werden kann:
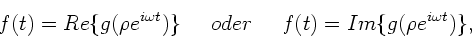 |
(16) |
dann kann die Reihenentwicklung für 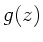 ,
,
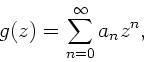 |
(17) |
benutzt werden, um eine Fourier- Reihe für 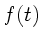 zu erhalten:
zu erhalten:
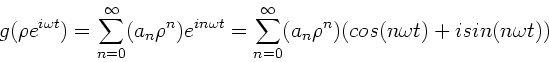 |
(18) |
Trennung nach Real- und Imaginärteil ergibt
(
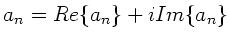 ):
):
Eine weitere Möglichkeit der Reihenentwicklung ist gegeben, wenn
in der Zeitfunktion  infinitesimale Parameter
infinitesimale Parameter  auftreten. Ein Beispiel möge dieses zeigen.
Sei
auftreten. Ein Beispiel möge dieses zeigen.
Sei
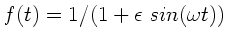 und
und
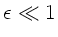 .
Da
.
Da
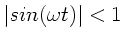 , kann man nach
, kann man nach
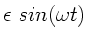 entwickeln:
entwickeln:
Bei dieser Art von Reihenentwicklungen muß man sich natürlich
darüber im Klaren sein, daß in höheren Termen von 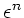 noch weitere Glieder mit
noch weitere Glieder mit
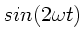 oder
oder
 auftreten können.
auftreten können.
Nichtperiodische Funktionen
Bei nichtperiodischen Funktionen wird aus dem diskreten
Frequenzspektrum ein kontinuierliches Frequenzspektrum:
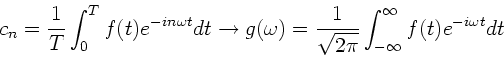 |
(24) |
Die Reihenentwicklung der Funktion 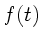 muß als Integral geschrieben
werden:
muß als Integral geschrieben
werden:
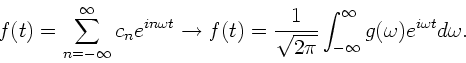 |
(25) |
Daß diese Ersetzungen richtig sind, ersieht man am einfachsten, wenn
man das Frequenzspektrum  wieder in das Integral für
wieder in das Integral für
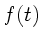 einsetzt:
einsetzt:
Da
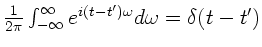 die Diracsche Deltafunktion ist, folgt
die Diracsche Deltafunktion ist, folgt
 |
(28) |
Aufgabe 1:
Wie groß sind die Amplituden der harmonischen Schwingungen, aus denen sich
die periodische Sägezahnkurve 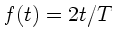 aufbaut ?
aufbaut ?
- Hinweis:
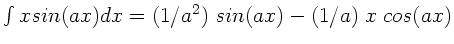

Aufgabe 2:
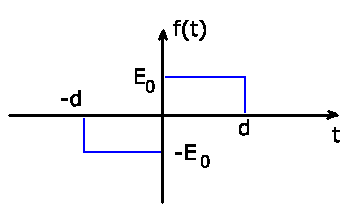
Berechnen Sie die Fourier- Transformierte der nichtperiodischen
Funktion 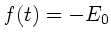 für
für 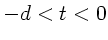 ,
,  für
für 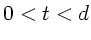 und
und
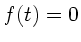 für
für  .
.
Aufgabe 3:
Bestimmen Sie die Fourierreihen Entwicklung für die Funktion
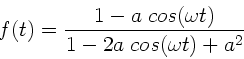 |
(29) |
- Hinweis: Diskutieren Sie die Potenzreihenentwicklung für
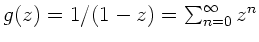 für
für 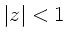 , wobei
, wobei 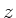 eine
komplexe Zahl ist.
eine
komplexe Zahl ist.
Lösungen zu den Rechenübungen am 4. November 1992.
Aufgabe 1:
Symmetrie von 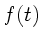 :
: 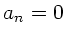 . Mit
. Mit
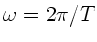 folgt:
folgt:
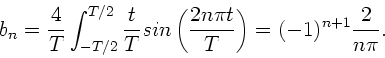 |
(30) |
Aufgabe 2:
Aufgabe 3:
Mit
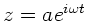 erhalten wir die Potenzreihen- Entwicklung:
erhalten wir die Potenzreihen- Entwicklung:
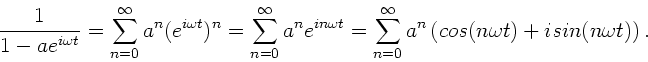 |
(34) |
Auf der linken Seite dieser Gleichung steht die imaginäre Einheit 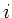 im Nenner. Um die linke Seite in Real und Imaginärteil trennen zu
können, muß die imaginäre Einheit in den Zähler gebracht werden.
Hierzu erweitern wir Zähler und Nenner mit dem komplex konjugierten
des Nenners :
im Nenner. Um die linke Seite in Real und Imaginärteil trennen zu
können, muß die imaginäre Einheit in den Zähler gebracht werden.
Hierzu erweitern wir Zähler und Nenner mit dem komplex konjugierten
des Nenners :
 :
:
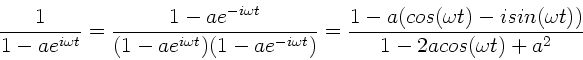 |
(35) |
Also:
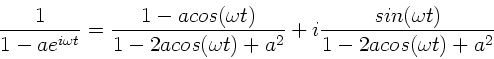 |
(36) |
Vergleich der Real- und Imaginärteile zeigt:
Harm Fesefeldt
2007-08-21
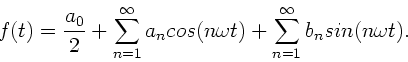
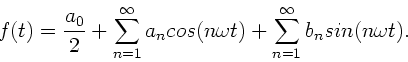
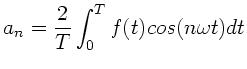
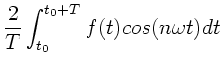
![$\displaystyle \frac{2}{T} \int_{0}^{T/2} [f(t)+f(-t)] cos(n\omega t) dt$](img9.gif)
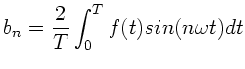
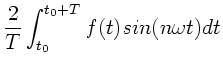
![$\displaystyle \frac{2}{T} \int_{0}^{T/2} [f(t)-f(-t)] sin(n\omega t) dt$](img12.gif)

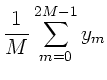

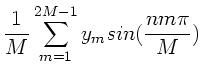

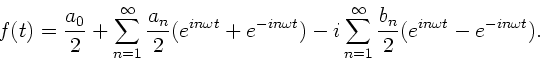
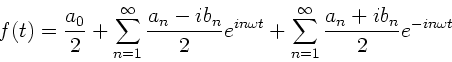
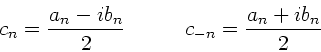
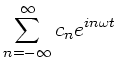
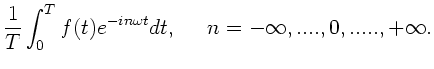
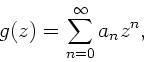
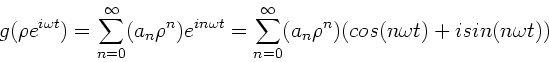
![$\displaystyle \sum_{n=0}^{\infty} \rho^{n}
[Re\{a_{n}\} cos(n\omega t) - Im\{a_{n}\} sin(n\omega t)]$](img41.gif)
![$\displaystyle \sum_{n=0}^{\infty} \rho^{n}
[Im\{a_{n}\} cos(n\omega t) + Re\{a_{n}\} sin(n\omega t)]$](img43.gif)
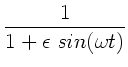
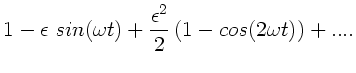
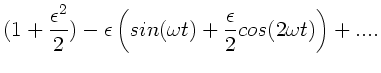
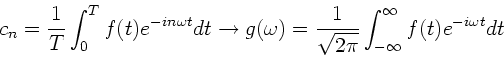
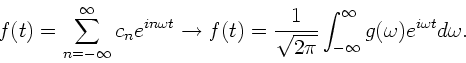

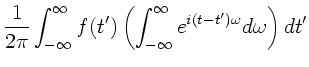

![]() für
für ![]() ,
, ![]() für
für ![]() und
und
![]() für
für ![]() .
.