Physik III, WS 1992/93
Übungen in der Übungsstunde am 21. Oktober 1992
Aufgabe 1:
Gegeben sei eine Welle der Form
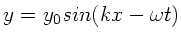 mit den
Parametern
mit den
Parametern
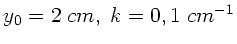 und
und
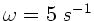 .
Berechnen Sie die a) Wellenlänge, b) Frequenz, c) Schwingungsdauer,
d) Phasengeschwindigkeit, e) Amplitude und f) Ausbreitungsrichtung.
Wie sieht die Funktion aus, wenn sich die identische Welle in
entgegengesetzter Richtung fortplanzt ?
.
Berechnen Sie die a) Wellenlänge, b) Frequenz, c) Schwingungsdauer,
d) Phasengeschwindigkeit, e) Amplitude und f) Ausbreitungsrichtung.
Wie sieht die Funktion aus, wenn sich die identische Welle in
entgegengesetzter Richtung fortplanzt ?
Aufgabe 2:
Zeigen Sie, daß
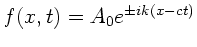 Lösungen der
Wellengleichung sind.
Lösungen der
Wellengleichung sind.
Aufgabe 3:
Gegeben ist das Wellenpaket zur Zeit 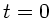 :
:
a) Wie lautet die Gleichung der Welle mit diesem Profil, die sich mit der
Geschwindigkeit
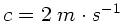 in positiver
in positiver 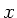 -Richtung
bewegt ?
-Richtung
bewegt ?
b) Zeigen Sie, daß diese Lösung die Wellengleichung erfüllt.
Aufgabe 4:
Eine harmonische, transversal polarisierte Welle laufe auf einem unendlich
langen Seil in positive 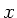 -Richtung.
-Richtung.
a) Zeigen Sie, daß ein Seilstückchen an der Stelle 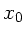 eine
harmonische Schwingung ausführt.
eine
harmonische Schwingung ausführt.
b) Wann erreicht ein solches Seilstückchen seine maximale
Geschwindigkeit ?
Lösung zu Aufgabe 1:
a)
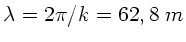 , b)
, b)
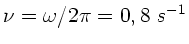 ,
c)
,
c)
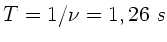 ,
,
d)
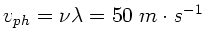 , e)
, e) 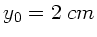 ,
f)
,
f) 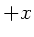 -Richtung.
-Richtung.
Entgegengesetze Richtung:
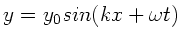 .
.
Lösung zu Aufgabe 2:
Man beachte hierbei die Definition der imaginären Einheit 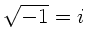 und
und 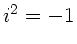 . Keine weitere Anleitung nötig !
. Keine weitere Anleitung nötig !
Lösung zu Aufgabe 3:
a)
b) Keine Anleitung nötig !
Lösung zu Aufgabe 4:
a) Bei
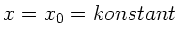 können wir eine harmonische Welle durch
können wir eine harmonische Welle durch
![$y(x_{0},t) = A_{0} sin[k(x_{0}-ct)]$](img21.gif) beschreiben. Diese Funktion löst die
DGL der harmonischen Schwingung:
beschreiben. Diese Funktion löst die
DGL der harmonischen Schwingung:
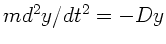 . Zweimalige
Differentation und Koeffizientenvergleich liefert
. Zweimalige
Differentation und Koeffizientenvergleich liefert
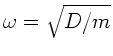 , wobei
, wobei 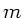 die Masse des Seilstückchens und
die Masse des Seilstückchens und
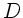 irgendeine Konstante ist, die die rücktreibende Kraft beschreibt.
irgendeine Konstante ist, die die rücktreibende Kraft beschreibt.
b) Geschwindigkeit des Seilstückchens
![$dy/dt = -kc A_{0} cos[k(x_{0}-ct)]$](img26.gif) . Die Maxima dieses Ausdrucks liegen bei
. Die Maxima dieses Ausdrucks liegen bei
![$\vert cos[k(x_{0}-ct)]\vert=1$](img27.gif) , d.h.
, d.h.
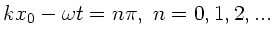 ,
also an den Stellen, wo die Schwingung
,
also an den Stellen, wo die Schwingung 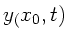 ihren Nulldurchgang
hat (analog Pendel).
ihren Nulldurchgang
hat (analog Pendel).
Harm Fesefeldt
2007-08-21
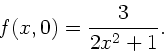
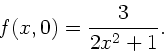
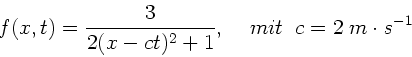
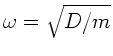 , wobei
, wobei