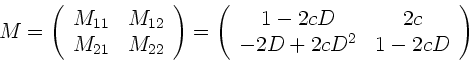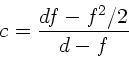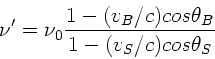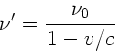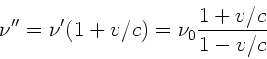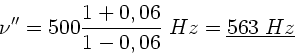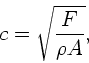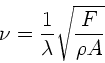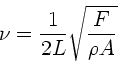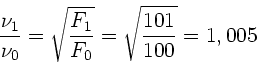Physik III, WS 1992/93
Lösungen zur Klausur
Besprechung: 10. Februar 1993
Aufgabe 1: (8 Punkte)
Der Gangunterschied zwischen den an Unterseite und Oberseite reflektierten
Strahlen ist
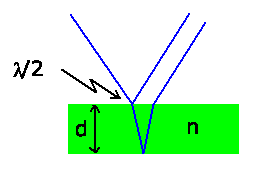
Verstärkung erhält man, wenn dieser Gangunterschied ein geradzahliges
Vielfaches der Wellenlänge ist:
Maximale Verstärkung erhält man also für die Wellenlängen:
Die folgende Tabelle zeigt die Werte der Wellenlängen in Abhängigkeit
von 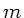 :
:
| m |
1 |
2 |
3 |
4 |
5 |
6 |
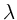 |
3000 nm |
1000 nm |
600 nm |
429 nm |
333 nm |
273 nm |
Im sichtbaren Teil des Spektrums liegen hierbei die beiden Wellenlängen
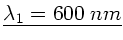 und
und
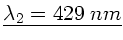 .
.
Aufgabe 2: (9 Punkte)
Zunächst ist klar, daß die Transmissionsachse des zweiten Polarisators
den Winkel
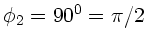 zur Polarisationsebene des einfallenden
Lichtes haben muß.
zur Polarisationsebene des einfallenden
Lichtes haben muß.
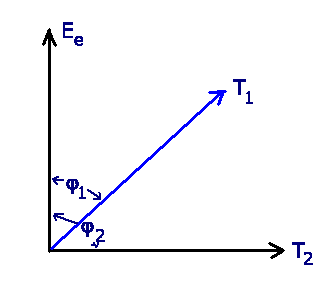
Der Winkel 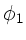 ist zunächst beliebig.
Die Intensität nach dem ersten Polarisator ist
ist zunächst beliebig.
Die Intensität nach dem ersten Polarisator ist
und nach dem zweiten Filter entsprechend
Da
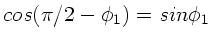 , kann man auch schreiben:
, kann man auch schreiben:
Die maximale Intensität folgt aus der Extremalbedingung
Die Lösung dieser Extremalbedingung kann im wesentlichen auf drei
Arten erfolgen. Einmal schreibt man die Gleichung für  in der Form
(siehe Formel in Aufgabenstellung):
in der Form
(siehe Formel in Aufgabenstellung):
![\begin{displaymath}
I = I_{0} \left[ cos\phi_{1} cos(\frac{\pi}{2}-\phi_{1}) \r...
...s(2\phi_{1}-\frac{\pi}{2}) +
cos(\frac{\pi}{2}) \right]^{2}
\end{displaymath}](img16.gif) |
(1) |
Dann folgt
![\begin{displaymath}
\frac{dI}{d\phi_{1}} = - I_{0} \left[ cos(2\phi_{1}-\frac{\...
...(\frac{\pi}{2}) \right] \; sin(2\phi_{1} - \frac{\pi}{2}) = 0
\end{displaymath}](img17.gif) |
(2) |
Dieses wird gelöst durch
Einfacher ist es allerdings, wenn man auf die Formel für 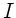
![\begin{displaymath}
I=I_{0} \left[ cos\phi_{1} \; cos(\frac{\pi}{2} -\phi_{1}) \right]^{2}
\end{displaymath}](img19.gif) |
(3) |
die Produktregel der Differentiation anwendet. Dieses ergibt
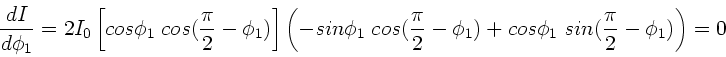 |
(4) |
und daher
Einige Kommilitonen haben einen besonders eleganten Weg gefunden.
Wegen
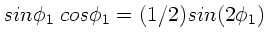 gilt
gilt
und daher
mit den Lösungen  oder
oder
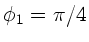 . Die erste
Lösung entspricht einem Minimum, die zweite einem Maximum.
Der Winkel ist also
. Die erste
Lösung entspricht einem Minimum, die zweite einem Maximum.
Der Winkel ist also
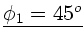 .
.
b) Die Intensität selbst folgt dann aus
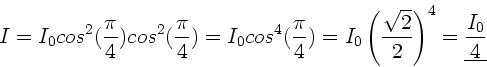 |
(5) |
Aufgabe 3: (8 Punkte)
Die allgemeine Formel zur Berechnung der Gruppengeschwindigkeit ist
Wegen
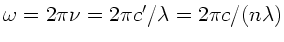 folgt
mit
folgt
mit
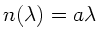 und
und
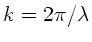 .
.
und
Weitere Lösungswege
Nach Vorlesung und Rechenübung vom 16.12.93 gilt auch
Diese Formel wurde ebenfalls bereits in der Vorlesung hergeleitet.
Wegen 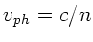 und
und
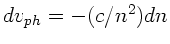 gilt dann
gilt dann
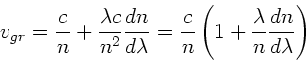 |
(6) |
Diese Formel wurde ebenfalls bereits in den Rechenübungen
am 16.12.93 hergeleitet. Wegen
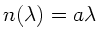 ergibt sich sofort
ergibt sich sofort
Aufgabe 4: (9 Punkte)
1. Lösung durch zweistufigen Abbildungsprozeß
Zunächst einmal muß der Spiegel aus der Abbildung entfernt werden.
Dazu muß die Abbildung einfach symmetrisch aufgeklappt werden, wobei
der Spiegel die Symmetrieebene ist. Die Richtigkeit dieses Vorgehens
wird in der zweiten Lösung mit Hilfe der Matrizen- Optik streng
bewiesen. In der folgenden Abbildung ist links das Auge als Objekt,
zwei identische Linsen 1 und 2 mit jeweils Abstand 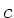 vom Spiegel,
sowie schließlich das Auge als Beobachter. In diesem allgemeinen
zweistufigen Prozeß ist als Nebenbedingung enthalten, daß die
Abstände Auge- Lupe auf beiden Seiten
vom Spiegel,
sowie schließlich das Auge als Beobachter. In diesem allgemeinen
zweistufigen Prozeß ist als Nebenbedingung enthalten, daß die
Abstände Auge- Lupe auf beiden Seiten 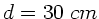 sind.
sind.
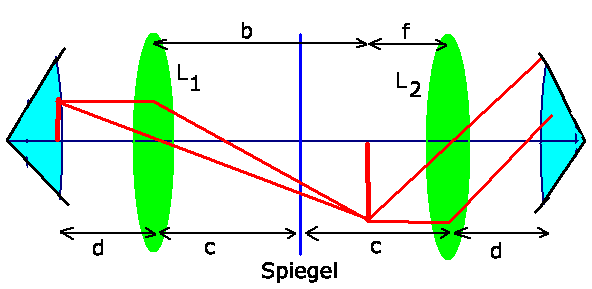
Als weitere Nebenbedingung muß beachtet werden, daß das Auge völlig
entspannt ist, d.h. auf Unendlich eingestellt ist. In diesem Fall muß
das Zwischenbild im Brennpunkt der Linse 2 sein. Daher gilt:
Die zweite Gleichung ist die Abbildungsgleichung der ersten Lupe.
Aus diesen beiden Gleichungen kann 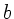 eliminiert und
eliminiert und 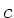 berechnet werden,
berechnet werden,
Einsetzen der Zahlenwerte (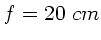 ,
, 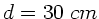 ) ergibt dann
) ergibt dann
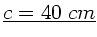 .
.
2. Lösung mit Hilfe der Matrizen- Optik
Die vorliegende Aufgabe kann streng mit Hilfe der Matrizen- Optik
behandelt werden. Die folgende Abbildung zeigt den Strahlengang.
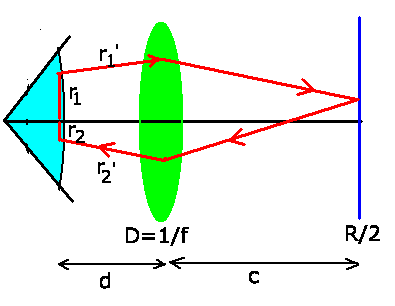
Die Transformationsgleichung ist:
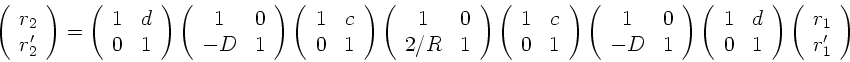 |
(7) |
Hierbei ist 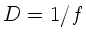 die Brechkraft der Lupe und
die Brechkraft der Lupe und 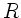 der Krümmungsradius
des Spiegels. Da
der Krümmungsradius
des Spiegels. Da 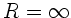 , folgt
, folgt 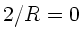 , sodaß die Reflexionsmatrix
am Spiegel zur Einheitsmatrix wird und weggelassen werden kann.
Die beiden Translationsmatrizen zwischen Lupe und Spiegel und zurück
können zusammengefaßt werden:
, sodaß die Reflexionsmatrix
am Spiegel zur Einheitsmatrix wird und weggelassen werden kann.
Die beiden Translationsmatrizen zwischen Lupe und Spiegel und zurück
können zusammengefaßt werden:
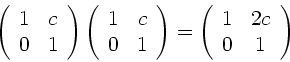 |
(8) |
Damit reduziert sich die Transformation zu
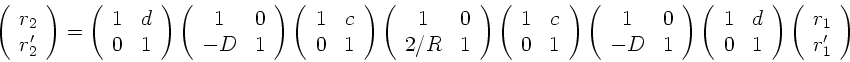 |
(9) |
mit der Systemmatrix
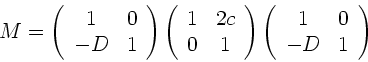 |
(10) |
Diese Transformation entspricht aber der folgenden zweistufigen
Abbildung,
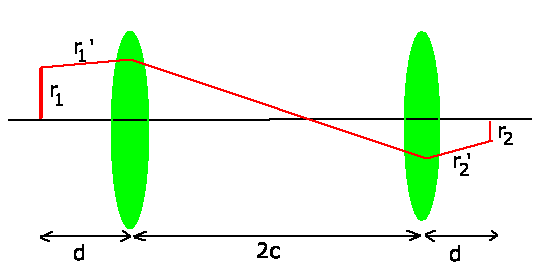
wie wir sie als Lösungsansatz bereits in der ersten Lösung verwendet haben.
Die Berechnung von 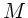 ergibt:
ergibt:
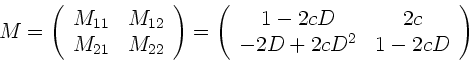 |
(11) |
und die Gesamttransformation wird zu
In diese Transformation muß jetzt noch die Bedingung des völlig
entspannten Auges eingearbeitet werden. Dieses bedeutet, daß ein
Lichtstrahl vom Punkt 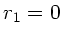 parallel zur optischen Achse in das
Auge zurückreflektiert wird (
parallel zur optischen Achse in das
Auge zurückreflektiert wird (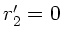 ), und zwar unabhängig
vom Winkel
), und zwar unabhängig
vom Winkel 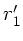 . Die zweite Gleichung wird unter diesen
Voraussetzungen
. Die zweite Gleichung wird unter diesen
Voraussetzungen
Einsetzen der Matrizelemente führt auf
Einsetzen von 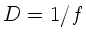 und Auflösen nach
und Auflösen nach 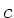 ergibt wie in der ersten
Lösung
ergibt wie in der ersten
Lösung
Aufgabe 5: (8 Punkte)
Die allgemeine Formel des Dopplereffektes ist (siehe Vorlesung):
Die Indizes ''B'' und ''S'' verweisen auf ''Beobachter'' und ''Sender''.
Die Geschwindigkeit des Zuges sei 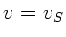 und seine Senderfrequenz
und seine Senderfrequenz
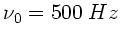 . Der Berg wirkt als Empfänger der Frequenz
. Der Berg wirkt als Empfänger der Frequenz
In diesem Fall ist 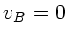 und
und 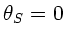 und damit
und damit
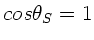 .
Wellen dieser Frequenz werden als Echo reflektiert. Relativ
zu diesem Sender bewegt sich der Zug mit der Geschwindigkeit
.
Wellen dieser Frequenz werden als Echo reflektiert. Relativ
zu diesem Sender bewegt sich der Zug mit der Geschwindigkeit 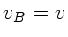 und
und
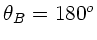 , also
, also
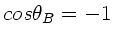 . Ein
Reisender im Zug hört daher das Echo mit der Frequenz
. Ein
Reisender im Zug hört daher das Echo mit der Frequenz
Wegen
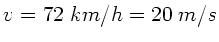 und
und 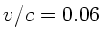 folgt
folgt
Aufgabe 6: (8 Punkte)
Die Phasengeschwindigkeit auf einer gespannten Saite ist nach Vorlesung
wobei 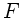 die die Spannung hervorrufende Kraft,
die die Spannung hervorrufende Kraft, 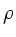 die Dichte und
die Dichte und
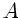 der Querschnitt ist. Wegen
der Querschnitt ist. Wegen 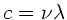 folgt auch
folgt auch
Bei der Grundschwingung der beiderseits eingespannten Saite ist die
Wellenlänge 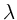 das Doppelte der Länge
das Doppelte der Länge 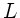 , daher auch
, daher auch
Da die Länge 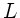 nicht verändert wird und die Saiten identisch sind
(gleiche Dichte und gleicher Querschnitt), folgt für das
Verhältnis der Frequenzen
nicht verändert wird und die Saiten identisch sind
(gleiche Dichte und gleicher Querschnitt), folgt für das
Verhältnis der Frequenzen
Mit
 ergibt sich für
ergibt sich für 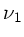 :
:
Die Schwebungsfrequenz schließlich ist
Harm Fesefeldt
2007-08-24
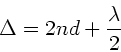
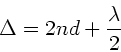

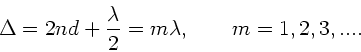
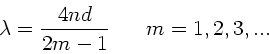

![]() ist zunächst beliebig.
Die Intensität nach dem ersten Polarisator ist
ist zunächst beliebig.
Die Intensität nach dem ersten Polarisator ist
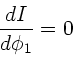
![\begin{displaymath}
I = I_{0} \left[ cos\phi_{1} cos(\frac{\pi}{2}-\phi_{1}) \r...
...s(2\phi_{1}-\frac{\pi}{2}) +
cos(\frac{\pi}{2}) \right]^{2}
\end{displaymath}](img16.gif)
![\begin{displaymath}
\frac{dI}{d\phi_{1}} = - I_{0} \left[ cos(2\phi_{1}-\frac{\...
...(\frac{\pi}{2}) \right] \; sin(2\phi_{1} - \frac{\pi}{2}) = 0
\end{displaymath}](img17.gif)
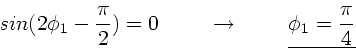
![\begin{displaymath}
I=I_{0} \left[ cos\phi_{1} \; cos(\frac{\pi}{2} -\phi_{1}) \right]^{2}
\end{displaymath}](img19.gif)
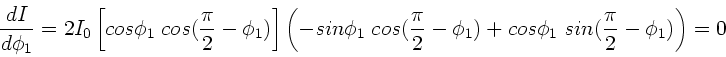
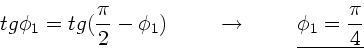
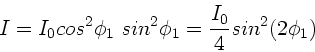
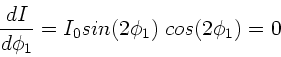
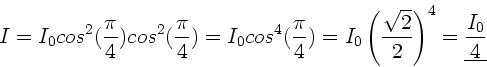
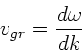
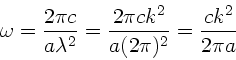
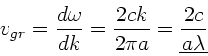
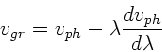
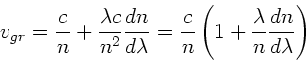
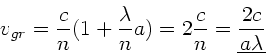

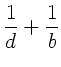
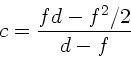

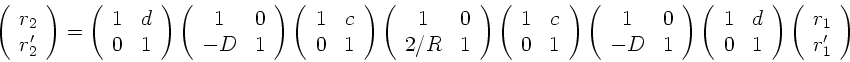
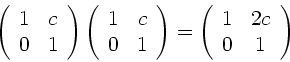
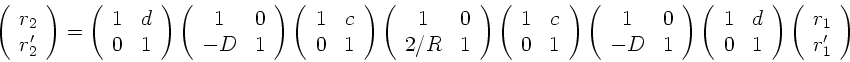
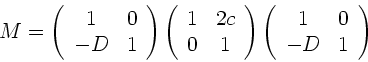

![]() ergibt:
ergibt: