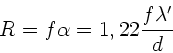Physik III, WS 1992/93
Lösungen zu den Übungen Nr.13
Besprechung: 10.Februar 1993
Aufgabe 1: (Bonusaufgabe) (6 Punkte)
a) Die Intensitätsverteilung am unendlich langen Einzelspalt ist nach
Vorlesung
mit
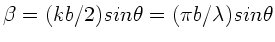 . Extrema
ergeben sich bei
. Extrema
ergeben sich bei
Minima ergeben sich für 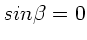 und
und 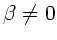 , d.h.
, d.h.
Maxima erhält man entsprechend für
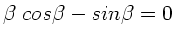 oder
oder
 . Letzteres wird erfüllt durch:
. Letzteres wird erfüllt durch:
Die Maxima liegen also nicht exakt zwischen den Minima, sondern
geringfügig zu kleineren Winkeln verschoben. Wegen
folgt für die Minima:
Für die ersten drei Nebenmaxima gilt:
b) Näherungsweise liegen die Maxima zwischen den Minima, d.h. bei
Dann ist aber
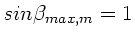 und daher
und daher
c) Die Intensität fällt auf die Hälfte ihres Wertes ab, wenn
oder
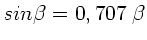 . Diese Gleichung wird gelöst durch
. Diese Gleichung wird gelöst durch
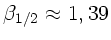 . Wegen
. Wegen
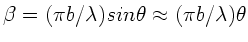 folgt:
folgt:
und
Aufgabe 2: (Bonusaufgabe) (6 Punkte)
Die Berechnung der Intensitätsverteilung bei der Beugung an ausgedehnten
Strukturen ist vom Prinzip her sehr einfach, die Komplikation liegt
häufig einzig und allein in der Berechnung komplizierter Integrale.
Wir diskutieren zunächst noch einmal ausführlich die Berechnung der
Intensitätsverteilung am unendlich langen Spalt und erweitern das Ergebnis
danach auf den Doppelspalt.
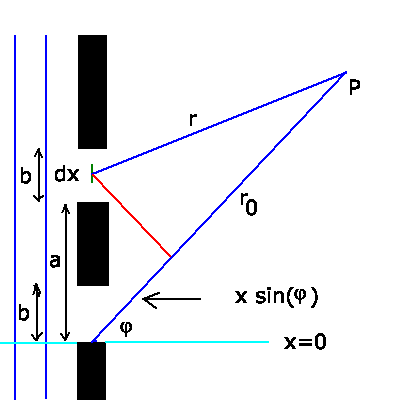
Eine ebene Lichtwelle der Wellenlänge 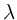 falle senkrecht auf
einen unendlich langen Spalt der Breite
falle senkrecht auf
einen unendlich langen Spalt der Breite 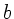 .
.
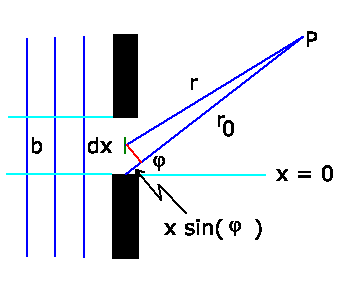
Jedes durch 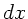 charakterisierte Flächenelement des Spaltes ist
nach Huygens Zentrum einer Kugelwelle. Die gesamte Lichterregung im
weit entfernten, durch den Beugungswinkel
charakterisierte Flächenelement des Spaltes ist
nach Huygens Zentrum einer Kugelwelle. Die gesamte Lichterregung im
weit entfernten, durch den Beugungswinkel 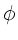 charakterisierten
Aufpunkt
charakterisierten
Aufpunkt 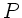 wird durch Integration über alle Elemente
wird durch Integration über alle Elemente 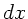 des Spaltes
erhalten, wobei die verschiedenen Phasen der Elementarwellen zu
berücksichtigen sind.
Wenn wir für die Größe der von
des Spaltes
erhalten, wobei die verschiedenen Phasen der Elementarwellen zu
berücksichtigen sind.
Wenn wir für die Größe der von 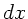 ausgehenden Wellenamplitude
den Ansatz
ausgehenden Wellenamplitude
den Ansatz
machen, dann ist die Elementarwelle im Punkt 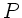 darstellbar durch
darstellbar durch
Hierbei ist allerdings bereits die Annahme eingeführt, daß alle
infinitesimalem Beiträge zur Welle im Punkt 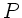 parallel sind.
Wegen des Vektorcharakters der Feldstärke
parallel sind.
Wegen des Vektorcharakters der Feldstärke 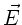 ist dieses eine
Näherung, die nur für
ist dieses eine
Näherung, die nur für 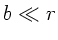 erfüllt ist. Ohne diese Näherung
werden die nachfolgend zu berechnenden Integrale außerordentlich
kompliziert. Mit der bereits eingeführten Näherung
erfüllt ist. Ohne diese Näherung
werden die nachfolgend zu berechnenden Integrale außerordentlich
kompliziert. Mit der bereits eingeführten Näherung
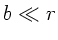 ist auch
ist auch
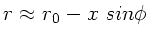 , daher
, daher
Diese Formel beendet den physikalischen Teil der Aufgabe, es folgt der
mathematische Teil. Die Gesamtamplitude im Aufpunkt 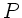 ergibt sich
aus der Summe (Integral) aller Teilamplituden der verschiedenen
Flächenelemente
ergibt sich
aus der Summe (Integral) aller Teilamplituden der verschiedenen
Flächenelemente 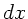 . Dieses Integration kann auf der reellen
Zahlengerade oder in der komplexen Ebene durchgeführt werden.
Wir zeigen zunächst die reelle Integration:
. Dieses Integration kann auf der reellen
Zahlengerade oder in der komplexen Ebene durchgeführt werden.
Wir zeigen zunächst die reelle Integration:
Dieses Integral wird gelöst durch
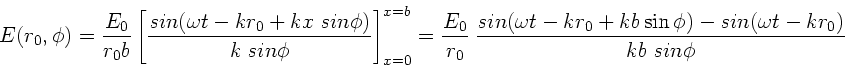 |
(1) |
Mit Hilfe trigonometrischer Formeln kann man zeigen, daß
Die Integration und die nachfolgenen Umrechnungen kann man vereinfachen,
wenn man die Feldstärke als Realteil einer komplexen Funktion schreibt.
Dieses Integral ist leicht auszuwerten und ergibt
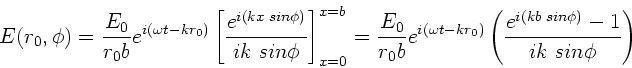 |
(2) |
 |
(3) |
Wegen
 folgt:
folgt:
Wir gehen zurück zum Realteil und erhalten:
also das gleiche Ergebnis wie oben. Die Intensität ist proportional
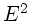 , gemittelt über die Zeit
, gemittelt über die Zeit 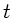 . Da allgemein
. Da allgemein
folgt in unserem Beispiel
Wegen
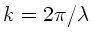 kann man dieses auch schreiben als:
kann man dieses auch schreiben als:
Die Erweiterung auf den Doppelspalt ist nun denkbar einfach, man muß
die Integration nur über beide Spalte erstrecken:
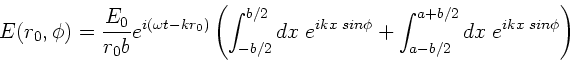 |
(4) |
Die Integration wird exakt wie beim Einzelspalt durchgeführt,
nur mit etwas mehr Schreibarbeit. Das Ergebnis ist:
mit
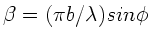 und
und
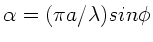 .
.
b) Skizze:
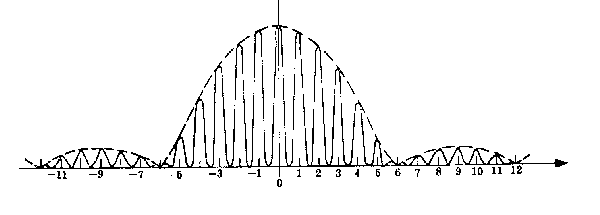
Aufgabe 3: (Bonusaufgabe) (4 Punkte)
Die Beugung an einer kreisförmigen Öffnung ergibt ein System
konzentrischer Maxima und Minima. Nach Vorlesung erscheint das erste
Minimum unter dem Winkel
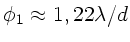 , wobei
, wobei
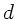 der Durchmesser der Öffnung ist. Daher folgt für den Radius
des Minimums auf der Netzhaut
der Durchmesser der Öffnung ist. Daher folgt für den Radius
des Minimums auf der Netzhaut
mit
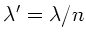 . Einsetzen der Zahlenwerte:
. Einsetzen der Zahlenwerte:
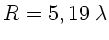 . Setzt man eine mittlere Wellenlänge von
. Setzt man eine mittlere Wellenlänge von
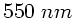 ein, so folgt
ein, so folgt
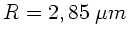 und für den Durchmesser
und für den Durchmesser
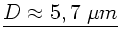 .
.
Aufgabe 4: (Bonusaufgabe) (4 Punkte)
Wegen
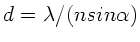 und
und 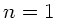 ,
,
 folgt
folgt
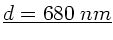 .
.
Harm Fesefeldt
2007-08-24
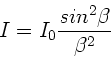
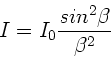
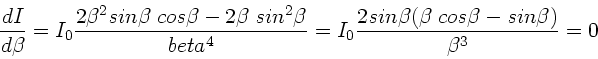
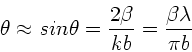
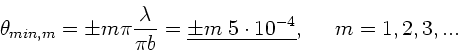
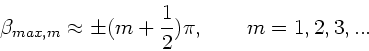
![\begin{displaymath}
I_{m} = I_{0} \frac{1}{\beta^{2}} = I_{0} \frac{1}{[(m+1/2)\pi]^{2}}
\end{displaymath}](img15.gif)
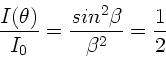

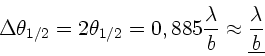

![]() charakterisierte Flächenelement des Spaltes ist
nach Huygens Zentrum einer Kugelwelle. Die gesamte Lichterregung im
weit entfernten, durch den Beugungswinkel
charakterisierte Flächenelement des Spaltes ist
nach Huygens Zentrum einer Kugelwelle. Die gesamte Lichterregung im
weit entfernten, durch den Beugungswinkel ![]() charakterisierten
Aufpunkt
charakterisierten
Aufpunkt ![]() wird durch Integration über alle Elemente
wird durch Integration über alle Elemente ![]() des Spaltes
erhalten, wobei die verschiedenen Phasen der Elementarwellen zu
berücksichtigen sind.
Wenn wir für die Größe der von
des Spaltes
erhalten, wobei die verschiedenen Phasen der Elementarwellen zu
berücksichtigen sind.
Wenn wir für die Größe der von ![]() ausgehenden Wellenamplitude
den Ansatz
ausgehenden Wellenamplitude
den Ansatz

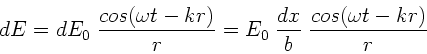
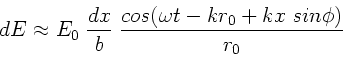
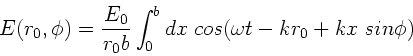
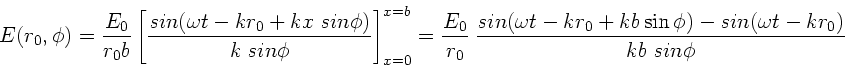

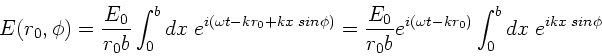
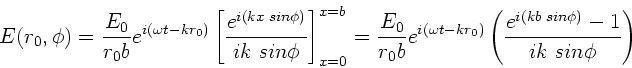

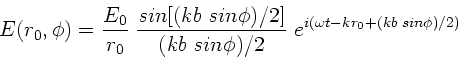
![\begin{displaymath}
E(r_{0},\phi) = \frac{E_{0}}{r_{0}} \frac{sin[(kb \; sin\ph...
...(kb \; sin\phi)/2} cos[\omega t -kr_{0} + (kb \; sin\phi)/2]
\end{displaymath}](img41.gif)
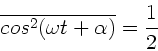
![\begin{displaymath}
I \sim \overline{E^{2}} = \frac{E_{0}^{2}}{r_{0}^{2}} \;
...
...\;
\frac{sin^{2}[(kb\; sin\phi)/2]}{[(kb\; sin\phi)/2]^{2}}
\end{displaymath}](img45.gif)
![\begin{displaymath}
I = I_{0} \;
\frac{sin^{2}[(\pi b \; sin\phi)/\lambda]}{[\pi b \; sin\phi)/\lambda]^{2}}
\end{displaymath}](img47.gif)

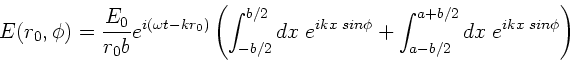
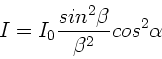

![]() , wobei
, wobei
![]() der Durchmesser der Öffnung ist. Daher folgt für den Radius
des Minimums auf der Netzhaut
der Durchmesser der Öffnung ist. Daher folgt für den Radius
des Minimums auf der Netzhaut