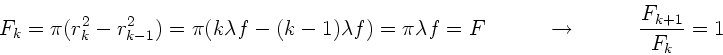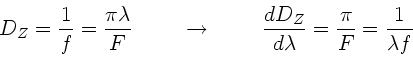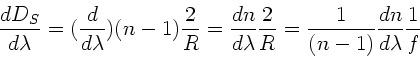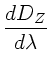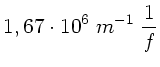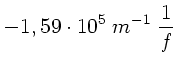Physik III, WS 1992/93
Lösungen zur Übung Nr. 12
Besprechung: 10. Februar 1993
Aufgabe 1: (5 Punkte)
a) Eine dünne Schicht reflektiert Licht einer bestimmten Wellenlänge
genau dann maximal, wenn die an der Ober- und Unterseite der Schicht
reflektierten Strahlen konstruktiv interferieren.
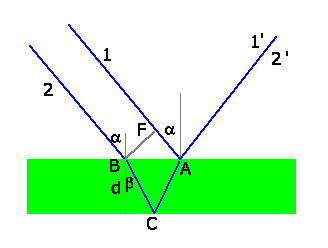
Der Gangunterschied ist
Hierbei wurde beachtet, daß bei Reflexion am dichteren Medium ein
Phasensprung von 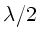 auftritt. Aus der Geometrie der Abbildung
folgt:
auftritt. Aus der Geometrie der Abbildung
folgt:
Mit dem Brechungsgesetz
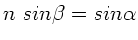 und einigen
weiteren Umformungen folgt:
und einigen
weiteren Umformungen folgt:
Damit Verstärkung auftritt, muß die Gangdifferenz ein Vielfaches der
Wellenlänge sein,
Daraus folgt
Die kleinstmögliche Schichtdicke ergibt sich für 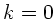 , also
, also
Für rotes Licht der Wellenlänge
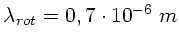 ,
Brechzahl
,
Brechzahl 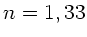 und Einfallswinkel
und Einfallswinkel
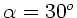 folgt:
folgt:
b) Für einen Einfallswinkel von
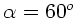 ergibt sich bei
sonst gleichen Bedingungen wie in Teil a):
ergibt sich bei
sonst gleichen Bedingungen wie in Teil a):
Diese Wellenlänge entspricht einer gelbgrünen Färbung.
Diskussion der Aufgabe
Die Zahlenangaben dieser Aufgabe wurden sorgfältig geprüft. Der Autor
dieser Musterlösungen ist kein Experte über Farbenlehre und insbesondere
über die physiologische Wahrnehmung von Farben. Bei einer exakten
Formulierung dieser Aufgabe hätte man Angaben über die spektrale
Intensitätsverteilung des einfallenden Lichtes und der spektralen
Sensitivität des beobachtenden Auges machen müssen. Die Wellenlänge
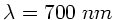 liegt jedoch am äußersten Ende des sichtbaren
Spektrums, mit einer kleinen Sensitivität des Auges. Falls diese
Wellenlänge verstärkt wird, werden notwendigerweise die anderen
sichtbaren Farben geschwächt. Wie weit diese allerdings geschwächt
werden, hängt von der spektralen Intensität der Quelle ab. Da man
trotzdem noch ''Rot'' sieht, dürfen die anderen Farben nicht
übermäßig stark im Spektrum vorkommen. Umgekehrt ist die Argumentation
bei Teil b). Hier muß man davon ausgehen, daß bei der Farbe Grün
die maximale Sensitivität des Auges ist. Sofern Grün überhaupt
im Spektrum vorkommt und darüber hinaus noch maximal verstärkt
wird, wird man die verbleibende Farbmischung wahrscheinlich als
grün empfinden. Im allgemeinen hängt natürlich der Farbeindruck von
der Mischung aller vorkommenden Farben ab.
liegt jedoch am äußersten Ende des sichtbaren
Spektrums, mit einer kleinen Sensitivität des Auges. Falls diese
Wellenlänge verstärkt wird, werden notwendigerweise die anderen
sichtbaren Farben geschwächt. Wie weit diese allerdings geschwächt
werden, hängt von der spektralen Intensität der Quelle ab. Da man
trotzdem noch ''Rot'' sieht, dürfen die anderen Farben nicht
übermäßig stark im Spektrum vorkommen. Umgekehrt ist die Argumentation
bei Teil b). Hier muß man davon ausgehen, daß bei der Farbe Grün
die maximale Sensitivität des Auges ist. Sofern Grün überhaupt
im Spektrum vorkommt und darüber hinaus noch maximal verstärkt
wird, wird man die verbleibende Farbmischung wahrscheinlich als
grün empfinden. Im allgemeinen hängt natürlich der Farbeindruck von
der Mischung aller vorkommenden Farben ab.
Aufgabe 2: (5 Punkte)
Die erforderliche Spiegelverschiebung 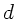 bis zum Verschwinden jeglicher
Interferenzen hängt von der Kohärenzlänge und damit von der
Linienbreite ab. Aus der gegebenen Linienbreite berechnet man zunächst
die Kohärenzlänge (siehe Rechenübungen vom 13.1.93):
bis zum Verschwinden jeglicher
Interferenzen hängt von der Kohärenzlänge und damit von der
Linienbreite ab. Aus der gegebenen Linienbreite berechnet man zunächst
die Kohärenzlänge (siehe Rechenübungen vom 13.1.93):
Wenn die optische Gangdifferenz 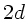 den Wert
den Wert 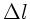 erreicht,
verschwinden die Interferenzen. Das ist der Fall, wenn
erreicht,
verschwinden die Interferenzen. Das ist der Fall, wenn
b) Eine Vergrößerung von 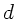 um
um 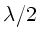 führt zu einer
Vergrößerung der optischen Gangdifferenz um
führt zu einer
Vergrößerung der optischen Gangdifferenz um 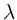 . Die Anzahl
. Die Anzahl
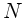 der Interferenzringe im Zentrum ist daher bei einer endlichen
Verschiebung
der Interferenzringe im Zentrum ist daher bei einer endlichen
Verschiebung 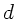 :
:
c) Die Frequenzstabilität ist definiert als (siehe Rechenübungen vom
13.1.93)
Daher folgt für die Kohärenzlänge:
Da
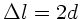 (siehe Teil a)), folgt
(siehe Teil a)), folgt
Aufgabe 3: (4 Punkte)
Wenn eine Spektrallinie der Wellenlänge 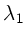 aus dem
Spektrum erster Ordnung unter dem Winkel
aus dem
Spektrum erster Ordnung unter dem Winkel 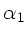 erscheint,
so gilt nach Vorlesung, mit der Gitterkonstanten
erscheint,
so gilt nach Vorlesung, mit der Gitterkonstanten 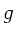 :
:
Entsprechend gilt für eine Spektrallinie 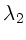 aus dem Spektrum
zweiter Ordnung:
aus dem Spektrum
zweiter Ordnung:
Beide Spektrallinien überdecken sich (
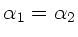 ), wenn
), wenn
Da das sichtbare Licht aber nur die Wellenlängen von 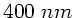 bis
bis
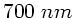 umfaßt, kann diese Bedingung nicht erfüllt
werden.
umfaßt, kann diese Bedingung nicht erfüllt
werden.
Aufgabe 4: (6 Punkte)
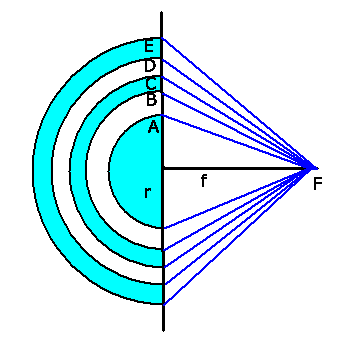
Läßt man eine ebene Welle senkrecht auf die Zonenplatte fallen,
so wirkt jedes Flächenelement eines freien Kreisringes als Zentrum
einer Kugelwelle (Huygenssches Prinzip). Diese Wellen sollen sich im
Brennpunkt verstärken, müssen also im Punkt 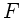 mit gleicher Phase
eintreffen. Diese Bedingung ist näherungsweise erfüllt, wenn
die Wege
mit gleicher Phase
eintreffen. Diese Bedingung ist näherungsweise erfüllt, wenn
die Wege 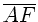 ,
, 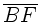 ,
, 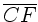 ,...sich
jeweils um
,...sich
jeweils um 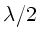 unterscheiden. Dieses führt auf die allgemeine
Bedingung
unterscheiden. Dieses führt auf die allgemeine
Bedingung
oder
Der zweite Term in der Klammer ist außerordentlich klein gegenüber 1,
daher
a) Für
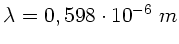 und
und 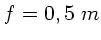 folgt
folgt
b) Der Flächeninhalt des 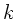 -ten Kreisringes ist
-ten Kreisringes ist
Die Flächeninhalte der Kreisringe sind also konstant und hängen nicht
von 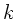 ab.
ab.
c) Die chromatische Aberration der Zonenlinse ist
Demgegenüber beträgt die chromatische Aberration einer Sammellinse
aus Glas:
Zahlenmäßig ergibt sich
Abgesehen vom Vorzeichen ist die chromatische Aberration bei der
Zonenplatte einen Faktor 10 größer als bei der normalen Glaslinse.
Da außerdem die Lichtstärke etwa einen Faktor 2 kleiner als bei
der Glaslinse ist, hat sich die Zonenplatte als optische
Linse nicht durchsetzen können. Trotzdem gibt es interessante
Anwendungen bei Radiowellen und akustischen Wellen.
Harm Fesefeldt
2007-08-24


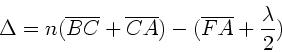
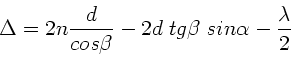
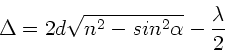
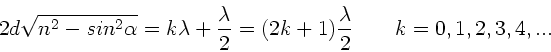
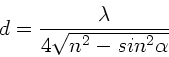
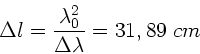
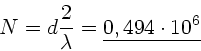
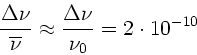
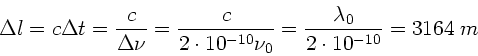
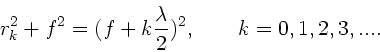
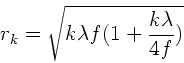

![]() und
und ![]() folgt
folgt