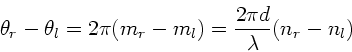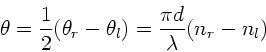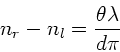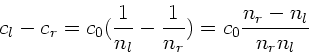Physik III, WS 1992/93
Lösungen zur Übung Nr. 11
Besprechung: 27. Januar 1993
Aufgabe 1: (5 Punkte)
Wir verwenden im folgenden die in der Aufgabenstellung angegebene
Richtung der Transmissionsachsen der Polarisatoren. Danach ist das
Licht hinter dem ersten Polarisator vertikal polarisiert, mit der
Intensität
Der Winkel zwischen den Transmissionsachsen der ersten beiden Polarisatoren
sei 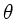 , dann folgt aus dem Gesetz von Malus:
, dann folgt aus dem Gesetz von Malus:
Der Winkel zwischen den beiden hinteren Polarisatoren ist 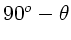 .
Nochmalige Anwendung von Malus Gesetz ergibt
.
Nochmalige Anwendung von Malus Gesetz ergibt
Mit Hilfe der Formel
erhält man:
Die maximale Intensität ist also
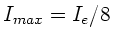 und die
Oszillationsfrequenz der Intensität ist
und die
Oszillationsfrequenz der Intensität ist
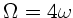 .
.
Aufgabe 2: (5 Punkte)
Diese Aufgabe wurde bereits ausführlich in der Vorlesung
(siehe Skript Seite 172-175) durchgerechnet, wobei für die
vorliegende Aufgabe lediglich eine kleine Modifikation notwendig ist.
In der Vorlesung wurde das 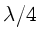 - Plättchen behandelt.
Dieses erzeugt aus einer linear polarisierten Welle eine zirkular
polarisierte Welle.
- Plättchen behandelt.
Dieses erzeugt aus einer linear polarisierten Welle eine zirkular
polarisierte Welle.
Setzen wir den Koordinatenursprung an die Vorderfläche des
Quarz- Plättchens, so ist die Feldstärke am Ort 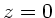 :
:
wobei die 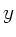 - Achse mit der Richtung der optischen Achse übereinstimmt.
Nach Durchgang des Lichts durch das Plättchen ergibt sich eine
Phasendifferenz zwischen der
- Achse mit der Richtung der optischen Achse übereinstimmt.
Nach Durchgang des Lichts durch das Plättchen ergibt sich eine
Phasendifferenz zwischen der 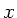 - und
- und 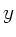 - Komponente von
(siehe Vorlesung):
- Komponente von
(siehe Vorlesung):
Um linear polarisiertes Licht zu erhalten, muß
Während sich für
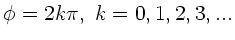 die Polarisationsebene
nicht ändert, ergibt sich für
die Polarisationsebene
nicht ändert, ergibt sich für
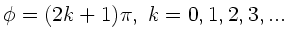 eine Drehung der Polarisationsebene um
eine Drehung der Polarisationsebene um 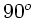 .
Wir müssen also fordern, daß
.
Wir müssen also fordern, daß
Daraus ergibt sich die notwendige Dicke 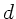 der Platte zu
der Platte zu
Einsetzen der Zahlenwerte:
Aufgabe 3: (5 Punkte)
Wir zerlegen die einfallende Welle in den ordentlichen und
außerordentlichen Strahl. Der ordentliche Strahl ist senkrecht zur
optischen Achse polarisiert, der außerordentliche Strahl parallel
zur optischen Achse. Beide Strahlen haben gleiche Richtung, sind jedoch
phasenverschoben. Beim Eintritt in das zweite Prisma, dessen optische
Achse nach Aufgabenstellung senkrecht zur optischen Achse des ersten
Prismas gerichtet sein sollte, wird der ordentliche Strahl zum
außerordentlichen Strahl und umgekehrt der außerordentliche Strahl
zum ordentlichen Strahl. Der Einfallswinkel bei der Brechung an der
Grenzfläche der beiden Prismen ist identisch mit dem Keilwinkel
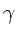 der Prismen (siehe untenstehende Skizze). Wir bezeichnen
mit dem Index 1 den im zweiten Prisma als ordentlichen Strahl
erscheinenden Lichtstrahl, umgekehrt mit dem Index 2 den im zweiten
Prisma als außerordentlichen Strahl erscheinenden Lichtstrahl.
Die weitere Bezeichnung der Winkel ist in der folgenden Skizze
angegeben.
Die Brechungsgesetze an der Grenzfläche der beiden Prismen lauten
der Prismen (siehe untenstehende Skizze). Wir bezeichnen
mit dem Index 1 den im zweiten Prisma als ordentlichen Strahl
erscheinenden Lichtstrahl, umgekehrt mit dem Index 2 den im zweiten
Prisma als außerordentlichen Strahl erscheinenden Lichtstrahl.
Die weitere Bezeichnung der Winkel ist in der folgenden Skizze
angegeben.
Die Brechungsgesetze an der Grenzfläche der beiden Prismen lauten
Numerisch folgt daraus, daß
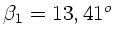 und
und
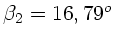 . Der Einfallswinkel auf die Begrenzungsfläche
des zweiten Prismas mit der Luft ist
. Der Einfallswinkel auf die Begrenzungsfläche
des zweiten Prismas mit der Luft ist
Nochmalige Anwendung des Brechungsgesetzes:
Der Winkel zwischen den beiden Lichtstrahlen 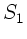 und
und 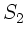 ist damit:
ist damit:
Die Strahlen sind wie in der folgenden Abbildung angegeben polarisiert.

Aufgabe 4: (5 Punkte)
a) Linear polarisiertes Licht läßt sich auffassen als Superposition
einer links- und rechtspolarisierten Welle. Die Zahl der Umläufe
der rechtspolarisierten Welle 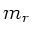 und linkspolarisierten Welle
und linkspolarisierten Welle
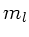 auf der Strecke
auf der Strecke 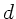 ist
ist
Die Differenz der Drehwinkel der entsprechenden Felder beträgt
Der resultierende Vektor liegt in der Winkelhalbierenden, hat also die
Drehung
erfahren. Daraus folgt:
Nach Aufgabenstellung ist
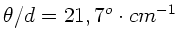 oder,
nach Umrechnung in Radian,
oder,
nach Umrechnung in Radian,
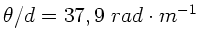 .
Die Differenz der Brechungsindizes ist also
.
Die Differenz der Brechungsindizes ist also
b) Die Differenz der Phasengeschwindigkeiten ist:
Bei Quarz ist der Unterschied der Brechungsindizes klein, sodaß
wir im Nenner einfach
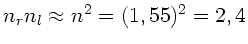 schreiben können (siehe Aufgabe 2). Dann ist
schreiben können (siehe Aufgabe 2). Dann ist
Harm Fesefeldt
2007-08-24
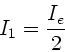
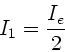
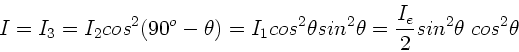
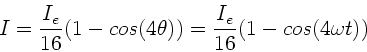
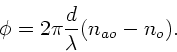
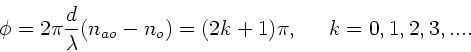
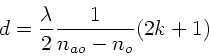

![]() und linkspolarisierten Welle
und linkspolarisierten Welle
![]() auf der Strecke
auf der Strecke ![]() ist
ist