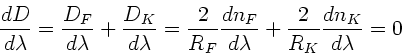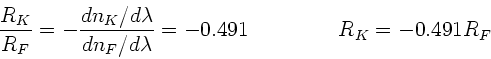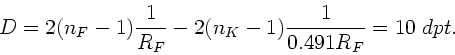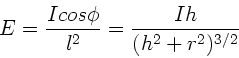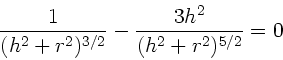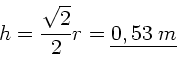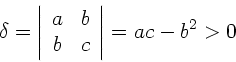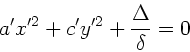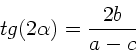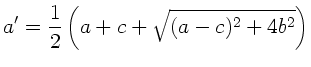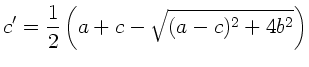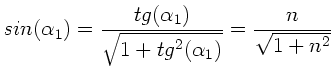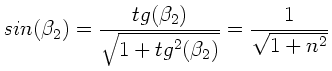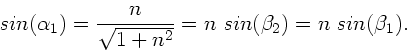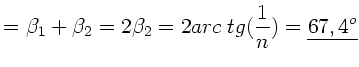Physik III, WS 1992/93
Lösungen zur Übung Nr. 10
Bonusübung
Besprechung: 20. Januar 1993
Aufgabe 1: (6 Punkte)
Die Gesamtbrechkraft eines zentrierten Systems kann durch die
Summe der Einzelbrechkräften dargestellt werden. Nach Aufgabenstellung
sollte die Gesamtbrechkraft 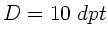 betragen. Daher
betragen. Daher
Die Brechkräfte der beiden Einzellinsen sind
wobei wir vorausgesetzt haben, daß die Linsen jeweils auf beiden
Seiten den gleichen Krümmungsradius haben. Die Vorzeichen von
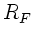 und
und 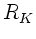 wurden dagegen noch offen gelassen.
Nach Vorlesung ist das Gesamtsystem achromatisch, wenn die Brennweite
und damit auch die Brechkraft nicht von der Wellenlänge abhängt,
d.h.
wurden dagegen noch offen gelassen.
Nach Vorlesung ist das Gesamtsystem achromatisch, wenn die Brennweite
und damit auch die Brechkraft nicht von der Wellenlänge abhängt,
d.h.
Daraus erhalten wir eine Nebenbedingung für die Krümmungsradien:
Zur Berechnung der Krümmungsradien verwenden wir die
Brechungsindizes bei der Natrium D-Linie und setzen die oben
abgeleitete Nebenbedingung ein:
Daraus folgt
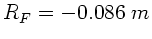 und
und
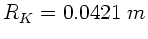 .
Für die Brennweiten folgt daraus
.
Für die Brennweiten folgt daraus
oder
Es handelt sich also um eine Kombination von einer Sammellinse
aus Kronglas und einer Zerstreuungslinse aus Flintglas.
Aufgabe 2: (4 Punkte)
Die Höhe der Lichtquelle über dem Tisch sei 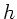 , der Abstand
der Lichtquelle vom Tischrand werde mit
, der Abstand
der Lichtquelle vom Tischrand werde mit 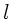 bezeichnet und der
Radius der Tischplatte mit
bezeichnet und der
Radius der Tischplatte mit
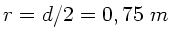 . Zur Berechnung
der Beleuchtungsstärke muß noch der Einfallswinkel
. Zur Berechnung
der Beleuchtungsstärke muß noch der Einfallswinkel 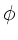 eingeführt werden (siehe Skizze)
eingeführt werden (siehe Skizze)
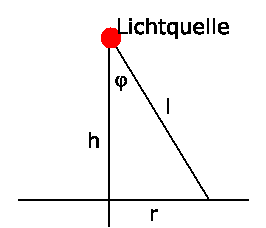
Dann gilt
Die Extremalbedingung 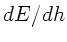 führt auf die Gleichung
führt auf die Gleichung
mit der Lösung:
Aufgabe 3: (4 Punkte)
Wir wählen als Fortpflanzungsrichtung wie üblich die z-Achse,
dann können wir die Komponenten der Feldstärke in x- und y- Richtung durch
beschreiben. Wegen
folgt auch
Die Form der allgemeinen Kegelschnitte,
ist genau dann eine Ellipse, wenn
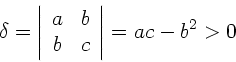 |
(1) |
ist (siehe irdendein Buch über Analytische Geometrie). In unserem
Fall ist
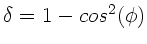 , was ersichtlich nur für
, was ersichtlich nur für
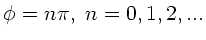 gleich Null ist, sonst immer größer
Null ist. Für
gleich Null ist, sonst immer größer
Null ist. Für 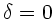 entartet die Ellipse zu einer Geraden.
Man erhält die Normalform der Ellipse,
entartet die Ellipse zu einer Geraden.
Man erhält die Normalform der Ellipse,
durch eine Drehung des Koordinatensystems um den Winkel 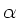 ,
der durch
,
der durch
gegeben ist. In unserem speziellen Fall ist 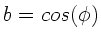 und
und
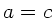 , daher
, daher
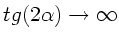 und
und
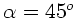 .
Der Winkel der Hauptachsen bezüglich der
.
Der Winkel der Hauptachsen bezüglich der 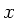 - Achse ist also immer
- Achse ist also immer
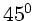 und nicht, wie manchmal in Prüfungen oder Klausuren
angenommen wird, gleich
und nicht, wie manchmal in Prüfungen oder Klausuren
angenommen wird, gleich 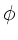 . Der Winkel
. Der Winkel 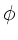 bestimmt das
Verhältnis der großen zur kleinen Hauptachse der Ellipse.
Allgemein gilt bei der oben durchgeführten Hauptachsentransformation:
bestimmt das
Verhältnis der großen zur kleinen Hauptachse der Ellipse.
Allgemein gilt bei der oben durchgeführten Hauptachsentransformation:
Für unseren speziellen Fall folgt hieraus:
Aufgabe 4: (6 Punkte)
Nach Vorlesung ist der reflektierte Strahl total polarisiert, wenn
der einfallende Strahl unter dem Brewster- Winkel einfällt.
Mit den Bezeichnungen der unten abgebildeten Skizze muß also sein:
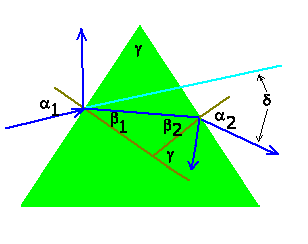
wobei wir den Brechungsindex 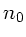 der umgebenden Luft gleich
1 gesetzt haben. Mit Hilfe trigonometrischer Umrechnungsformeln kann
man dies auch schreiben:
der umgebenden Luft gleich
1 gesetzt haben. Mit Hilfe trigonometrischer Umrechnungsformeln kann
man dies auch schreiben:
Außerdem gilt an der ersten brechenden Fläche das Brechungsgesetz:
Daher gilt auch:
Die Bedingung, daß beide reflektierten Strahlen total polarisiert
sind, ist also nur zu erreichen, wenn der Strahlendurchgang
symmetrisch ist (
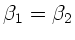 ). Mit Hilfe der allgemeinen
trigonometrischen Formeln
). Mit Hilfe der allgemeinen
trigonometrischen Formeln
ergeben sich der Reihe nach die folgenden Antworten (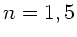 ):
):
Harm Fesefeldt
2007-08-24