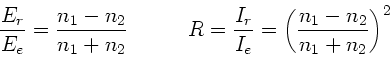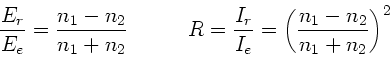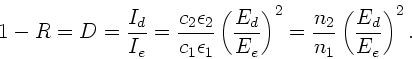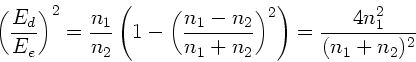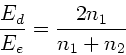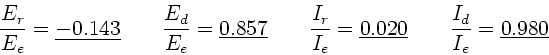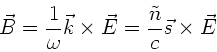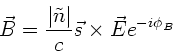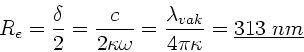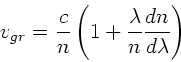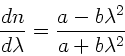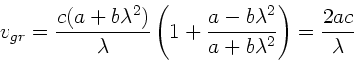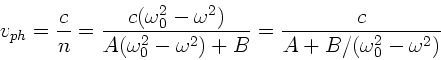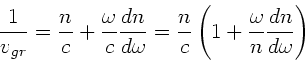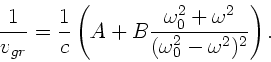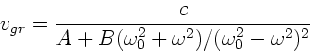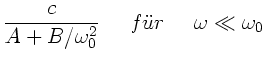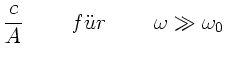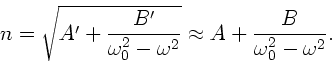Physik III, WS 1992/93
Lösungen zur Übung Nr. 9
Besprechung: 20. Januar 1993
Aufgabe 1: (5 Punkte)
Nach Vorlsesung ist zunächst
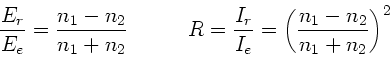 |
(1) |
Für die durchgelassene Intensität wurde hergeleitet:
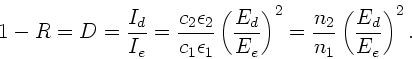 |
(2) |
Daraus folgt:
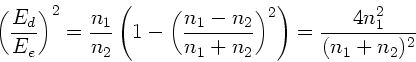 |
(3) |
und daher
Einsetzen der Zahlenwerte ergibt
Aufgabe 2: (5 Punkte)
Für die elektromagnetische Welle benutzen wir den Ansatz
wobei die Wellenzahl 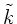 komplex ist, da der Brechungsindex
komplex ist, da der Brechungsindex
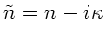 komplex ist. Da
komplex ist. Da
können wir die elektrische Feldstärke schreiben als
wobei wir zur Abkürzung
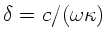 gesetzt haben.
gesetzt haben.
a) Das Magnetfeld 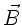 ist nach Maxwell in der folgenden Form
an die elektrische Feldstärke gekoppelt:
ist nach Maxwell in der folgenden Form
an die elektrische Feldstärke gekoppelt:
wobei 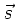 ein Einheitsvektor in Richtung der Ausbreitung
ist. Mit
ein Einheitsvektor in Richtung der Ausbreitung
ist. Mit
folgt
Der Phasenwinkel ist also
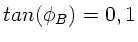 oder
oder
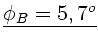 .
.
b) Die Intensität ist proportional zu 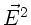 . Daher
. Daher
Die Intensität ist also bei der Strecke
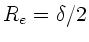 auf den
auf den
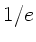 - ten Teil abgesunken. Zahlenwerte:
- ten Teil abgesunken. Zahlenwerte:
Dieses Ergebnis zeigt, daß schon bei ziemlich kleinen
Absorptionskoeffizienten die Eindringtiefe der Lichtwelle in der
Größenordnung oder kleiner als eine Wellenlänge ist. Daher
verliert nicht nur der Brechungsindex seine Bedeutung, sondern
insbesondere auch die Phasen- und Gruppengeschwindigkeit. Für
Wellen mit einer Ausdehnung kleiner als eine Wellenlänge kann
eine Phasengeschwindigkeit nicht mehr definiert werden.
Aufgabe 3: (5 Punkte)
Die Dispersionsformel 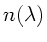 ist als Funktion der Wellenlänge
ist als Funktion der Wellenlänge
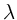 in dem Material angegeben. Wir verwenden daher die in den
Rechenübungen vom 16.12.92 angegebene Formel
in dem Material angegeben. Wir verwenden daher die in den
Rechenübungen vom 16.12.92 angegebene Formel
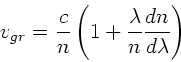 |
(4) |
Wegen
folgt
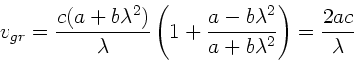 |
(5) |
Die Gruppengeschwindigkeit ist also umgekehrt proportional zu
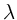 . Damit
. Damit 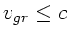 , muß
, muß
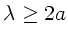 sein.
Die angegebene Formel für die Dispersion kann also nur für einen
beschränkten Wellenlängenbereich gelten.
sein.
Die angegebene Formel für die Dispersion kann also nur für einen
beschränkten Wellenlängenbereich gelten.
Aufgabe 4: (5 Punkte)
Der Brechungsindex ist als Funktion der Frequenz gegeben.
Für die Phasengeschwindigkeit folgt:
Zur Berechnung der Gruppengeschwindigkeit
verwenden wir die in den Rechenübungen vom 16.12.92 angegbene
Formel
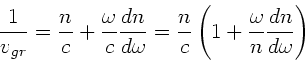 |
(6) |
Auswertung der Formel ergibt
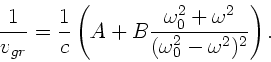 |
(7) |
und daher
Zur Anfertigung der Skizze bemerken wir zunächst, daß für
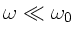 und
und
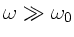 die folgenden
Grenzwerte angenommen werden:
die folgenden
Grenzwerte angenommen werden:
Im übrigen ist die Phasengeschwindigkeit durch 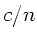 gegeben.
Für
gegeben.
Für
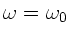 ist
ist
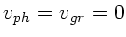 . Die
Phasengeschwindigkeit wird sogar kleiner Null bei
. Die
Phasengeschwindigkeit wird sogar kleiner Null bei 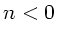 und springt
von
und springt
von 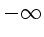 nach
nach 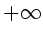 bei
bei 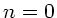 . Die Gruppengeschwindigkeit
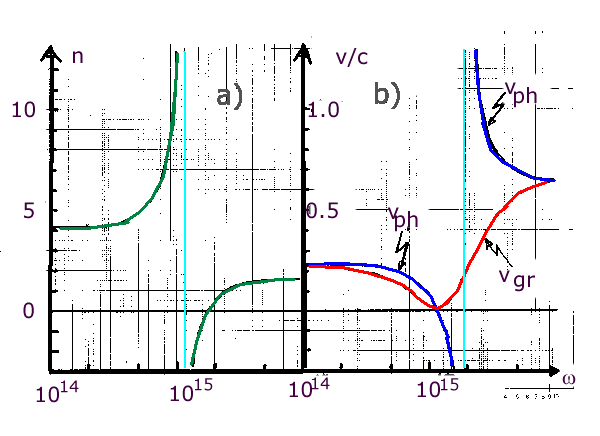
dagegen ist immer größer Null. Hieraus ergibt sich das in Bild
a) und b) angedeutete Verhalten für
. Die Gruppengeschwindigkeit
dagegen ist immer größer Null. Hieraus ergibt sich das in Bild
a) und b) angedeutete Verhalten für 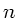 ,
, 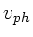 und
und 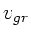 .
Es ist klar, daß in der Resonanz selbst der Brechungsindex durch
die angegebene Formel nicht beschrieben wird, da der
Dämpfungsparameter vernachlässigt wurde. Insbesondere kann
.
Es ist klar, daß in der Resonanz selbst der Brechungsindex durch
die angegebene Formel nicht beschrieben wird, da der
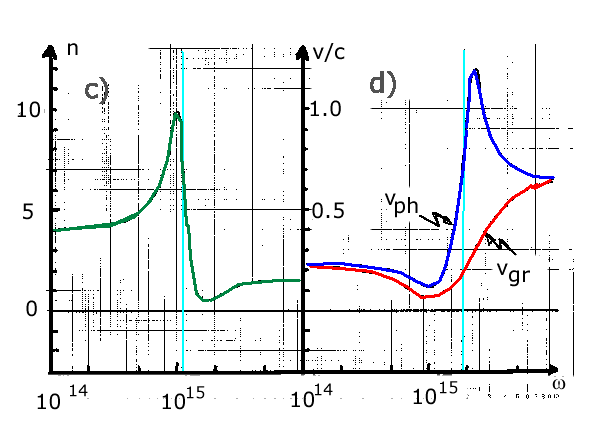
Dämpfungsparameter vernachlässigt wurde. Insbesondere kann 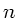 nicht kleiner Null werden. Aus den Skizzen a) und b) kann aber
durch Extrapolation sofort auf das wirkliche Verhalten geschlossen
werden. Diese Extrapolationen sind in den Skizzen c) und d) gezeigt.
Im übrigen muß darauf hingewiesen werden, daß die hier benutzte
Formel für den Brechungsindex eine Näherung für große Werte von
nicht kleiner Null werden. Aus den Skizzen a) und b) kann aber
durch Extrapolation sofort auf das wirkliche Verhalten geschlossen
werden. Diese Extrapolationen sind in den Skizzen c) und d) gezeigt.
Im übrigen muß darauf hingewiesen werden, daß die hier benutzte
Formel für den Brechungsindex eine Näherung für große Werte von
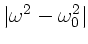 ist:
ist:
In der genaueren Näherungsformel kann 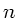 aber nicht negativ, sondern
höchstens imaginär werden. Darüber hinaus weisen wir nochmals darauf
hin, daß in der Resonanz die Eindringtiefe in das Medium in der
Größenordnung oder kleiner als eine Wellenlänge ist (siehe Aufgabe 2),
sodaß die Größen Brechungsindex und Geschwindigkeit keine Bedeutung
mehr haben.
aber nicht negativ, sondern
höchstens imaginär werden. Darüber hinaus weisen wir nochmals darauf
hin, daß in der Resonanz die Eindringtiefe in das Medium in der
Größenordnung oder kleiner als eine Wellenlänge ist (siehe Aufgabe 2),
sodaß die Größen Brechungsindex und Geschwindigkeit keine Bedeutung
mehr haben.
Harm Fesefeldt
2007-08-23