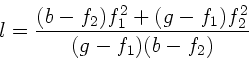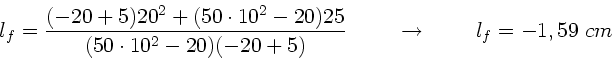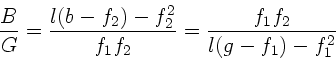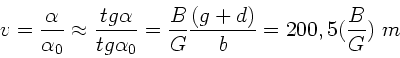Physik III, WS 1992/93
Lösungen zur Übung Nr. 8
Besprechung: 13. Januar 1993
Aufgabe 1: (4 Punkte)
Die Brechkraft 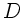 einer Linse in einem umgebendem Material mit
Brechungsindex
einer Linse in einem umgebendem Material mit
Brechungsindex 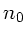 ist:
ist:
Für Luft also:
In Wasser gilt also:
Zahlenwerte:
Aufgabe 2: (5 Punkte)
Ein Strahlenbündel konvergiert in einem Punkt 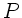 . Das heißt mit
anderen Worten, daß der Punkt
. Das heißt mit
anderen Worten, daß der Punkt 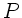 das Bild einer nicht nicht
näher bezeichneten Linse oder eines optischen Systems ist. Dieses
Zwischenbild wird jetzt als Gegenstand mit der Zerstreuungslinse weiter
abgebildet. Schiebt man die Zerstreuungslinse vor dem Punkt
das Bild einer nicht nicht
näher bezeichneten Linse oder eines optischen Systems ist. Dieses
Zwischenbild wird jetzt als Gegenstand mit der Zerstreuungslinse weiter
abgebildet. Schiebt man die Zerstreuungslinse vor dem Punkt 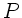 in
den Strahlengang, ist die Gegenstandsweite
in
den Strahlengang, ist die Gegenstandsweite 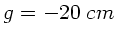 negativ, stellt man
die Zertreuungslinse hinter dem Punkt
negativ, stellt man
die Zertreuungslinse hinter dem Punkt 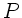 in den Strahlengang, so
ist die Gegenstandsweite
in den Strahlengang, so
ist die Gegenstandsweite 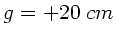 positiv. Daher
positiv. Daher
Unser Ergebnis ist also:
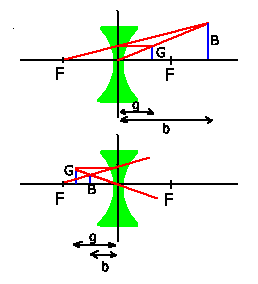
Im Fall a) befindet sich Gegenstand und Bild hinter der Linse, im Fall
b) befindet sich Gegenstand und Bild vor der Linse.
Aufgabe 3: (5 Punkte)
In der Vorlesung wurden Vergrößerungen einer Lupe bestimmt, wenn
das beobachtende Auge sich einmal im Brennpunkt der Lupe und
zum anderen direkt vor der Lupe
befindet. In dieser Aufgabe diskutieren wir noch einmal die
Vergrößerung, wenn der Abstand des Auges von der Lupe eine
beliebige Entfernung 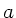 beträgt. Die Vergrößerung der
Lupe war in der Vorlesung definiert als
beträgt. Die Vergrößerung der
Lupe war in der Vorlesung definiert als
Die folgende Skizze veranschaulicht noch einmal diese Definition.
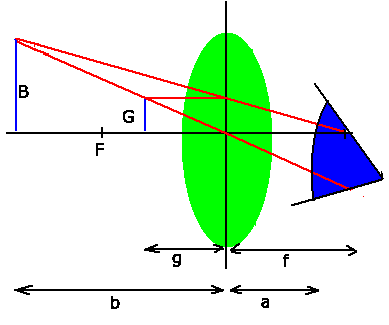
Wir bezeichnen den Abstand des Auges von der Lupe mit 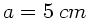 ,
die deutliche Sehweite mit
,
die deutliche Sehweite mit 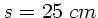 . Mit den Bezeichnungen der
obigen Abbildung ist dann:
. Mit den Bezeichnungen der
obigen Abbildung ist dann:
und daher (mit 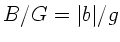 ):
):
Die letzte Formel setzen wir in die Abbildungsgleichung ein:
Zahlenwerte:
Anmerkung zur Definition der Vergrößerung
Die in der Vorlesung angegebene Definition der Vergrößerung ist
die allgemein übliche. Dennoch wird in einigen Büchern (z.B.
Bergmann-Schäfer) die Vergrößerung anders definiert, und zwar
als das Verhältinis der Sehwinkel mit Lupe und ohne Lupe, aber
jeweils bei der gleichen Sehweite 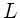 , die nicht unbedingt mit
der deutlichen Sehweite übereinzustimmen braucht. In diesem Fall
ist die Vergrößerung der Lupe identisch mit dem Abbildungsmaßstab
, die nicht unbedingt mit
der deutlichen Sehweite übereinzustimmen braucht. In diesem Fall
ist die Vergrößerung der Lupe identisch mit dem Abbildungsmaßstab
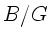 . Daher auch
. Daher auch
Wer diese Definition der Vergrößerung benutzt hat, erhält
für die Brennweite
Wir raten allerdings dringend davon ab, diese Definition in einer
möglichen Klausuraufgabe oder in Prüfungen zu verwenden.
Aufgabe 4: (6 Punkte)
In der Vorlesung wurde das Fernrohr für den Fall einer unendlichen
Gegenstandsweite diskutiert. In diese Aufgabe soll das Fernrohr
bei endlicher Gegenstandsweite diskutiert werden.
a) Zunächst berechnen wir die Brechkraft des Objektivs. Wegen
ist
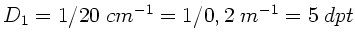 . Die
Brennweiten sind
. Die
Brennweiten sind
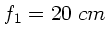 ,
,
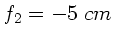 .
Mit der in den Rechenübungen am 9.12.92 abgeleiteten Newtonsche Form der
Abbildungsgleichung
.
Mit der in den Rechenübungen am 9.12.92 abgeleiteten Newtonsche Form der
Abbildungsgleichung
![\begin{displaymath}
\left[ g- \frac{f_{1}(f_{1}+l)}{l} \right] \left[ b
-\frac...
...2}+l)}{l} \right] = \left( \frac{f_{1} f_{2}}{l}
\right)^{2}
\end{displaymath}](img37.gif) |
(1) |
folgt nach Multiplikation der Gleichung mit 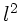 und
Ausmultiplizieren der Klammern:
und
Ausmultiplizieren der Klammern:
Die Gegenstandsweite ist
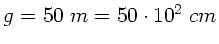 .
Normalerweise sind Fernrohre so konstruiert, daß sich das Auge
in der Brennweite des Okulars befindet (siehe Vorlesung).
Da das Bild in der deutlichen Sehweite von 25
.
Normalerweise sind Fernrohre so konstruiert, daß sich das Auge
in der Brennweite des Okulars befindet (siehe Vorlesung).
Da das Bild in der deutlichen Sehweite von 25
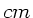 sein soll, muß
sein soll, muß
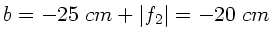 sein.
Man könnte das Auge aber auch direkt vor das Okular bringen.
In diesem Fall kann
sein.
Man könnte das Auge aber auch direkt vor das Okular bringen.
In diesem Fall kann 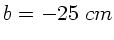 gesetzt werden. Wir rechnen im folgenden
beide Fälle durch und unterscheiden die Ergebnisse mit dem Index
gesetzt werden. Wir rechnen im folgenden
beide Fälle durch und unterscheiden die Ergebnisse mit dem Index 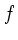 (Auge in Brennweite des Okulars) und Index 0 (Auge direkt vor dem
Okular).
Einsetzen der Zahlenwerte führt auf
(Auge in Brennweite des Okulars) und Index 0 (Auge direkt vor dem
Okular).
Einsetzen der Zahlenwerte führt auf
Daher ist der Abstand von Objektiv und Okular:
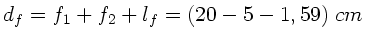 oder
oder
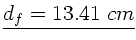
Entsprechend gilt für den Fall des Auges direkt vor dem Okular:
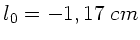 ,
,
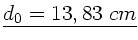 .
Der Unterschied ist also klein.
.
Der Unterschied ist also klein.
b) Zur Berechnung des Abbildungsmaßstabs benutzen wir eine der
in den Rechenübungen angegebenen Formeln:
Zur Überprüfung der Rechnung ist es empfehlenswert, den
Abbildungsmaßstab mit beiden Formeln zu berechnen. Einsetzen
der Zahlenwerte:
Das Bild ist also etwas weniger als 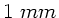 groß, also gerade noch in der deutlichen Sehweite sichtbar. Die
Vergrößerung ist dagegen (siehe Vorlesung):
groß, also gerade noch in der deutlichen Sehweite sichtbar. Die
Vergrößerung ist dagegen (siehe Vorlesung):
Dieses ergibt Vergrößerungen zwischen 2,4 und 3,2, je nachdem wo sich
das Auge befindet. Der Hersteller gibt natürlich die Vergrößerung
bei unendlicher Gegenstandsweite an. Diese beträgt nach Vorlesung
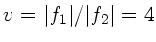 .
.
Harm Fesefeldt
2007-08-22
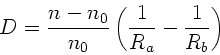
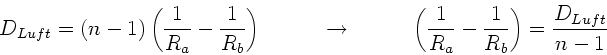
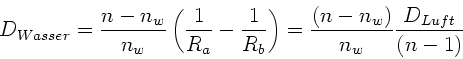
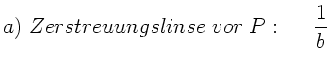
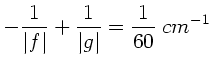
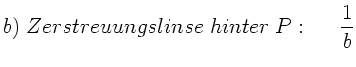
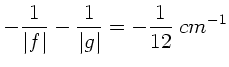

![]() beträgt. Die Vergrößerung der
Lupe war in der Vorlesung definiert als
beträgt. Die Vergrößerung der
Lupe war in der Vorlesung definiert als
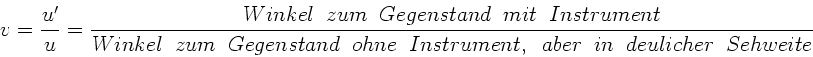

![]() ,
die deutliche Sehweite mit
,
die deutliche Sehweite mit ![]() . Mit den Bezeichnungen der
obigen Abbildung ist dann:
. Mit den Bezeichnungen der
obigen Abbildung ist dann:
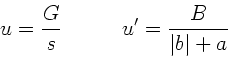
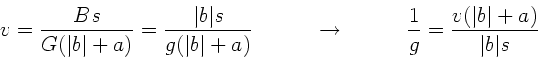
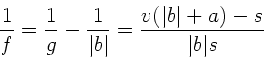
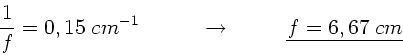
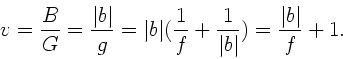
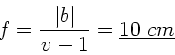
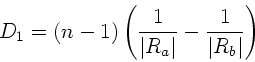
![\begin{displaymath}
\left[ g- \frac{f_{1}(f_{1}+l)}{l} \right] \left[ b
-\frac...
...2}+l)}{l} \right] = \left( \frac{f_{1} f_{2}}{l}
\right)^{2}
\end{displaymath}](img37.gif)