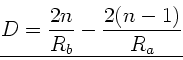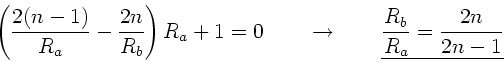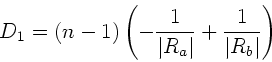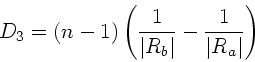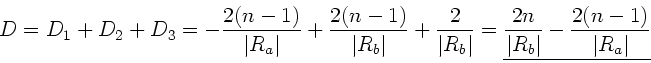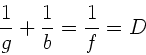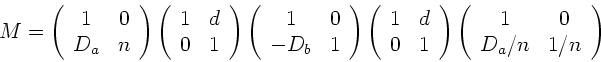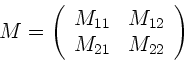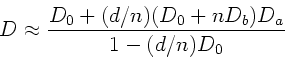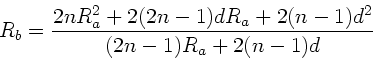Physik III, WS 1992/93
Lösungen zur Übung Nr. 7
Besprechung: 16. Dezember 1992
Aufgabe 1: (5 Punkte)
Die folgende Skizze zeigt den Strahlenverlauf und die Bezeichnung der
Winkel.
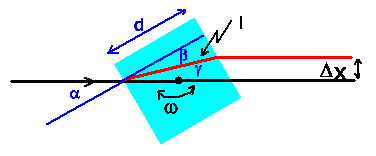
Man entnimmt folgende Zusammenhänge
Außerdem gilt das Brechungsgesetz
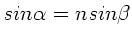 , daher auch
, daher auch
Hieraus folgt der Reihe nach für die Abweichung 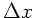 :
:
a) Die Abweichung 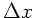 ist Null für
ist Null für 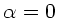 , d.h. für
senkrechten Einfall auf die Vorderfläche. Der Winkel
, d.h. für
senkrechten Einfall auf die Vorderfläche. Der Winkel 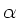 geht
von
geht
von 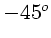 bis
bis 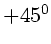 , wobei das Vorzeichen wechselt, sobald
der Lichtstrahl an der Kante des Würfels auftritt.
Die maximale Auslenkung erhält man also für
, wobei das Vorzeichen wechselt, sobald
der Lichtstrahl an der Kante des Würfels auftritt.
Die maximale Auslenkung erhält man also für
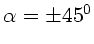 .
.
Zahlenwerte:
b) Zur Diskussion der Strahlauslenkung bei Rotation des Würfels mit
konstanter Winkelgeschwindigkeit 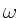 setzen wir
setzen wir
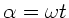 . Wie oben bereits diskutiert, wechselt die
Ablenkung
. Wie oben bereits diskutiert, wechselt die
Ablenkung 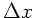 bei
bei
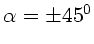 das Vorzeichen, daher
schreiben wir
das Vorzeichen, daher
schreiben wir
Die folgende Grafik zeigt diese Funktion.
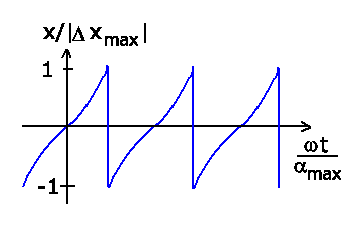
Aufgabe 2: (5 Punkte)
a) In der folgenden Abbildung sind der Einfallswinkel 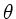 , der
Brechungswinkel
, der
Brechungswinkel 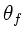 an der Stirnfläche der Faser und der
Winkel
an der Stirnfläche der Faser und der
Winkel 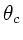 der Totalreflektion an der Begrenzungsfläche von Faser und
Mantel skizziert.
der Totalreflektion an der Begrenzungsfläche von Faser und
Mantel skizziert.
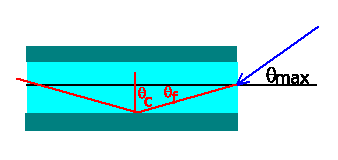
Der kritische Winkel der Totalreflektion ist
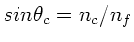 . Für alle Winkel größer als dieser
Winkel erhält man zusätzlich einen gebrochenen Strahl im Punkt
. Für alle Winkel größer als dieser
Winkel erhält man zusätzlich einen gebrochenen Strahl im Punkt  .
Aus der Geometrie ersieht man, daß
.
Aus der Geometrie ersieht man, daß
und daher
Einsetzen in das Brechungsgesetz am Punkt  führt auf
führt auf
Zahlenwerte:
b) In der folgenden Skizze zeigen wir das Kabel mit einem
Krümmungsradius  . Wir definieren den Radius bis zur
Mitte des Kabels. Falls jemand den Radius als Abstand zur inneren
Mantelfläche (
. Wir definieren den Radius bis zur
Mitte des Kabels. Falls jemand den Radius als Abstand zur inneren
Mantelfläche (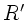 , siehe obige Abbildung) oder zur äußeren Mantelfläche
(
, siehe obige Abbildung) oder zur äußeren Mantelfläche
(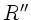 ) definiert hat, so
ändern sich die Ergebnisse geringfügig.
) definiert hat, so
ändern sich die Ergebnisse geringfügig.
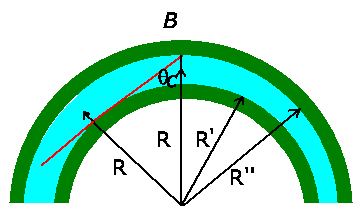
Aus der Geometrie ersieht man, daß der Winkel am Punkte 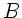 nicht
kleiner werden darf als
nicht
kleiner werden darf als
wobei 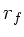 der Radius der Faser ist. Daher:
der Radius der Faser ist. Daher:
Zahlenwerte:
Der Krümmungsradius ist bei dieser Aufgabe nicht ganz eindeutig definiert
(siehe oben). Falls man den Radius 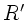 bis zur inneren Mantelfläche
als Krümmungsradius
genommen hat, so folgt
bis zur inneren Mantelfläche
als Krümmungsradius
genommen hat, so folgt
Wenn umgekehrt der Radius 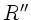 bis zur äußeren Mantelfläche als
Krümmungsradius definiert wurde, so gilt:
bis zur äußeren Mantelfläche als
Krümmungsradius definiert wurde, so gilt:
Aufgabe 3: (4 Punkte)
a) Wir benutzen die Abbildungsgleichung
Da
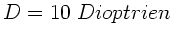 , ist
, ist
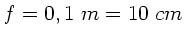 . Mit
. Mit 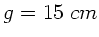 folgt
folgt
Nach Vorlesung ist
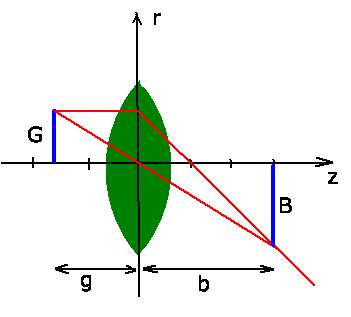
b) Zur Konstruktion des Strahlenganges muß man eine Skalierung
der Achsen vornehmen, da die Bild- und Gegenstandsgrößen sehr viel
kleiner als die Bild- und Gegenstandsweiten sind.
In der folgenden Zeichnung ist die  Achse
im Verhältnis
Achse
im Verhältnis 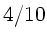 gegenüber der
gegenüber der 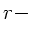 Achse gestaucht.
Üblicherweise zeichnet man den Strahlengang eines achsenparallelen
Einfallsstrahls, eines Strahls durch die Mitte der Linse und einen
Strahl durch den vorderen Brennpunkt, der die Linse nach der Brechung
parallel zur optischen Achse verläßt.
Achse gestaucht.
Üblicherweise zeichnet man den Strahlengang eines achsenparallelen
Einfallsstrahls, eines Strahls durch die Mitte der Linse und einen
Strahl durch den vorderen Brennpunkt, der die Linse nach der Brechung
parallel zur optischen Achse verläßt.
Aufgabe 4: (6 Punkte)
Lösung mit der Matrizen-Optik.
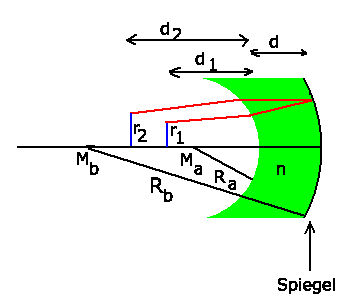
Wir behandeln diese Aufgabe zunächst mit der Matrizen- Optik (siehe
Rechenübungen vom 2.12.92) und zeichnen
daher den Strahlengang eines beliebigen Lichtstrahls durch die Linse.
Die Transformationsformel lautet ausführlich geschrieben:
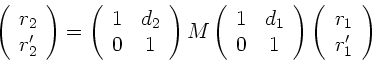 |
(1) |
mit der Linsenmatrix
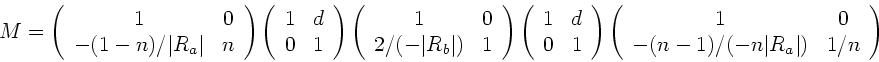 |
(2) |
Da nach Aufgabenstellung 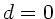 gesetzt werden sollte, werden
die beiden Translationsmatrizen durch die Linse zu Einheitsmatrizen,
können also weggelassen werden. Wir diskutieren die verbleibenden
Matrizen noch einmal von rechts nach links. Die erste Matrix auf der
rechten Seite beschreibt die Brechung des einfallenden Strahls.
Hier ist
gesetzt werden sollte, werden
die beiden Translationsmatrizen durch die Linse zu Einheitsmatrizen,
können also weggelassen werden. Wir diskutieren die verbleibenden
Matrizen noch einmal von rechts nach links. Die erste Matrix auf der
rechten Seite beschreibt die Brechung des einfallenden Strahls.
Hier ist 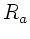 negativ zu nehmen, da dem Lichtstrahl die Fläche
konkav erscheint. Außerdem ist
negativ zu nehmen, da dem Lichtstrahl die Fläche
konkav erscheint. Außerdem ist 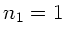 und
und 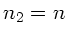 . Die mittlere
Matrix beschreibt die Reflexion am Spiegel. Hier ist
. Die mittlere
Matrix beschreibt die Reflexion am Spiegel. Hier ist 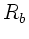 negativ, da
der Strahl die Fläche konkav sieht. Nach der Reflexion kehrt der
Strahl zurück zur Begrenzungsfläche zwischen Glas und Luft. Hier
ist jetzt aber
negativ, da
der Strahl die Fläche konkav sieht. Nach der Reflexion kehrt der
Strahl zurück zur Begrenzungsfläche zwischen Glas und Luft. Hier
ist jetzt aber 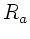 positiv einzusetzen, da der Strahl die
Begrenzungsfläche konvex sieht. Außerdem ist
positiv einzusetzen, da der Strahl die
Begrenzungsfläche konvex sieht. Außerdem ist 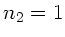 und
und
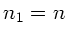 . In der obigen Formel haben wir die Vorzeichen bereits
explizit angeschrieben, sodaß in den weiteren Rechnungen
. In der obigen Formel haben wir die Vorzeichen bereits
explizit angeschrieben, sodaß in den weiteren Rechnungen
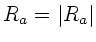 und
und 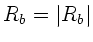 positiv sind. Mit den Abkürzungen
positiv sind. Mit den Abkürzungen
können wir die Linsenmatrix schreiben als
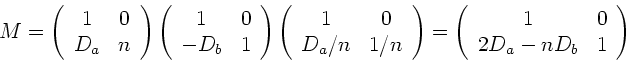 |
(3) |
Die Elemente der Matrix 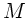 sind also
sind also
Die weitere Auswertung der Transformation liefert
a) Achsenparallele Strahlen (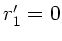 ) schneiden nach der Brechung
(
) schneiden nach der Brechung
(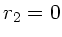 ) die optische Achse im Abstand
) die optische Achse im Abstand 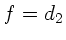 von der Linse,
wobei
von der Linse,
wobei 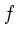 die Brennweite ist. Daher folgt aus der ersten
Transformationsformel:
die Brennweite ist. Daher folgt aus der ersten
Transformationsformel:
oder auch, nach Einsetzen der Abkürzungen:
b) Eine Lichtquelle im Punkt 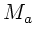 auf der optischen Achse
hat den Abstand
auf der optischen Achse
hat den Abstand 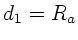 von der Linsenbegrenzung. Außerdem
ist
von der Linsenbegrenzung. Außerdem
ist 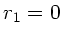 . Alle Strahlen von diesem Punkt sollen nach Brechung
und Reflektion die Steigung
. Alle Strahlen von diesem Punkt sollen nach Brechung
und Reflektion die Steigung 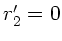 haben. Wir setzen dieses in
die zweite Transformationsformel ein und erhalten
haben. Wir setzen dieses in
die zweite Transformationsformel ein und erhalten
Einsetzen der Ausdrücke für 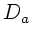 und
und 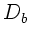 ergibt:
ergibt:
Lösung mit zentrierten Systemen
a) Man kann dieses Problem auch mit dem Satz behandeln, der aussagt,
daß sich bei zentrierten optischen Systemen die Brechkräfte
einfach addieren. Allerdings muß man sorgfältig auf die Vorzeichen
der Krümmungsradien achten.
Wir entfernen den Spiegel gedanklich von der Linsenoberfläche:
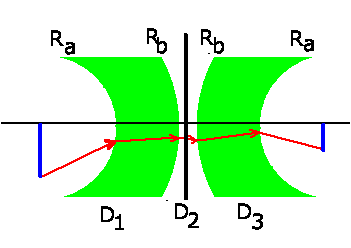
Der Lichtstrahl sieht beim Hinweg eine Linse mit zwei konkaven
Bregenzungsflächen und der Brechkraft:
wobei wir die Vorzeichenkonventionen bereits angebracht haben.
Beim Rückweg dagegen sieht das Licht eine Linse mit zwei konvexen
Begrenzungsflächen und der Brechkraft:
(siehe auch Vorzeichenkonvention der Rechenübungen vom 9.12.92,
Seite 4). Der Spiegel hat eine Brechkraft von
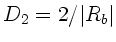 .
Insgesamt erhalten wir
.
Insgesamt erhalten wir
b) Setzen wir in der Abbildungsgleichung
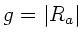 und
und 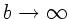 , so folgt das gleiche Ergebnis
wie oben für das Verhältnis der Radien.
, so folgt das gleiche Ergebnis
wie oben für das Verhältnis der Radien.
Die allgemeine Lösung
Die allgemeine Lösung für nichtverschwindende Dicke 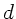 der Linse
ist ohne die Methoden der Matrizen- Optik kaum lösbar. Für den
interessierten Leser skizzieren wir kurz noch einmal den
Lösungsweg. Bei der Linsenmatrix müssen wir zwei Translationen
einschieben:
der Linse
ist ohne die Methoden der Matrizen- Optik kaum lösbar. Für den
interessierten Leser skizzieren wir kurz noch einmal den
Lösungsweg. Bei der Linsenmatrix müssen wir zwei Translationen
einschieben:
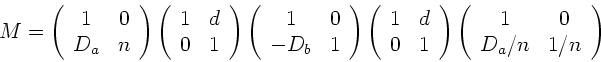 |
(4) |
Stures Ausmultiplizieren der Matrizen führt auf
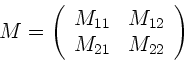 |
(5) |
mit
Ersichtlich geht für 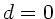 diese Linsenmatrix in die Matrix
für dünne Linsen über.
Die Gesamtabbildung lautet dann (siehe Rechenübungen):
diese Linsenmatrix in die Matrix
für dünne Linsen über.
Die Gesamtabbildung lautet dann (siehe Rechenübungen):
Die Brechkraft ist allgemein
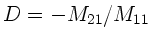 (siehe Rechenübungen).
Wir verzichten hier darauf, den allgemeinen Ausdruck explizit
hinzuschreiben. Falls man allerdings die Glieder mit
(siehe Rechenübungen).
Wir verzichten hier darauf, den allgemeinen Ausdruck explizit
hinzuschreiben. Falls man allerdings die Glieder mit 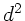 vernachlässigt, erhält man einen Ausdruck in erster Ordnung
für
vernachlässigt, erhält man einen Ausdruck in erster Ordnung
für 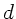 . Setzen wir als Abkürzung
. Setzen wir als Abkürzung
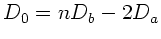 , so ist
, so ist
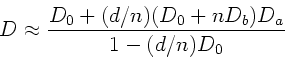 |
(6) |
Diese Formel geht für 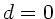 in
in 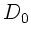 , die Brechkraft für die
dünne Linse, über.
Für praktische Anwendungen ist jedoch die Frage
von Teil b) außerordentlich wichtig, dient diese Spiegellinse
doch als Strahler. Wir setzen
, die Brechkraft für die
dünne Linse, über.
Für praktische Anwendungen ist jedoch die Frage
von Teil b) außerordentlich wichtig, dient diese Spiegellinse
doch als Strahler. Wir setzen 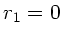 ,
, 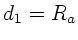 und
und
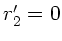 , dann erhalten wir
, dann erhalten wir
Einsetzen der Ausdrücke für 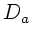 und
und 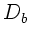 in die Matrixelemente
in die Matrixelemente
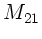 und
und 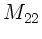 liefert dann nach einer etwas mühsamen Rechnung
liefert dann nach einer etwas mühsamen Rechnung
Dieser Ausdruck ist für 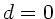 offensichtlich identisch mit unser
speziellen Lösung (siehe oben). Diese Formel ist im
Bergmann-Schäfer Band III (Optik), 8.Auflage, Seite 115,
angegeben.
offensichtlich identisch mit unser
speziellen Lösung (siehe oben). Diese Formel ist im
Bergmann-Schäfer Band III (Optik), 8.Auflage, Seite 115,
angegeben.
Harm Fesefeldt
2007-08-22


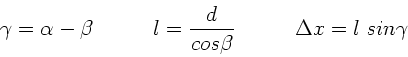
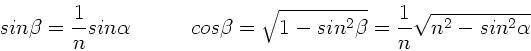
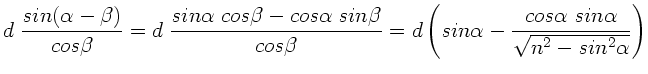
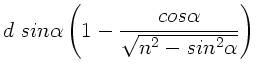
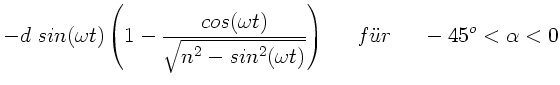
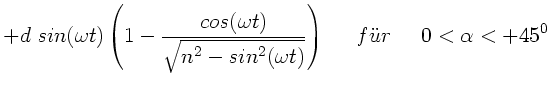
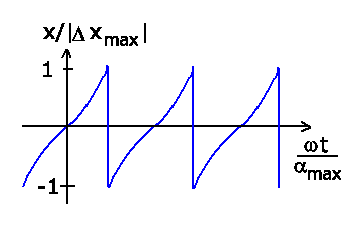
![]() , der
Brechungswinkel
, der
Brechungswinkel ![]() an der Stirnfläche der Faser und der
Winkel
an der Stirnfläche der Faser und der
Winkel ![]() der Totalreflektion an der Begrenzungsfläche von Faser und
Mantel skizziert.
der Totalreflektion an der Begrenzungsfläche von Faser und
Mantel skizziert. 
![]() . Für alle Winkel größer als dieser
Winkel erhält man zusätzlich einen gebrochenen Strahl im Punkt
. Für alle Winkel größer als dieser
Winkel erhält man zusätzlich einen gebrochenen Strahl im Punkt ![]() .
Aus der Geometrie ersieht man, daß
.
Aus der Geometrie ersieht man, daß
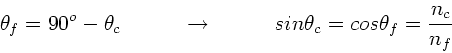
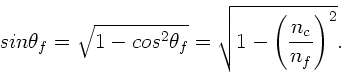
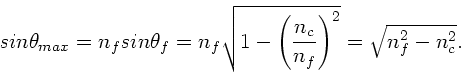

![]() nicht
kleiner werden darf als
nicht
kleiner werden darf als
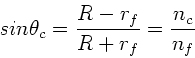
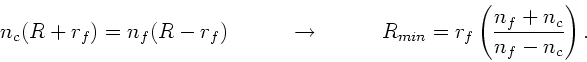
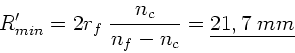
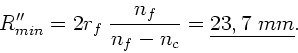
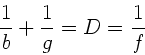

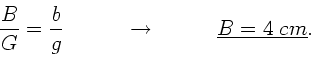


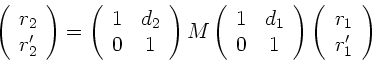
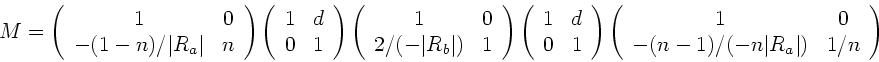
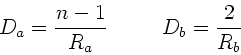
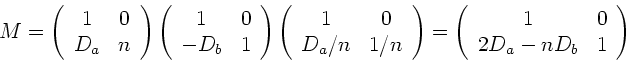
![\begin{displaymath}
0 = [1 + (2D_{a} - nD_{b}) f] r_{1} \; \; \; \; \; \; \; \;...
...
\; \; \; \; \; \; \; \; \; \; D=\frac{1}{f} = nD_{b}-2D_{a}
\end{displaymath}](img70.gif)