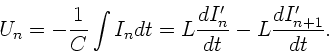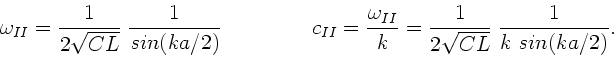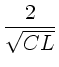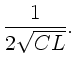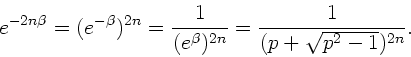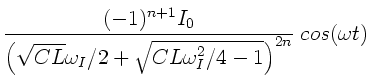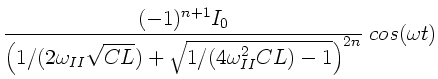Physik III, WS 1992/93
Lösungen zur Übung Nr. 5
Besprechung: 2. Dezember 1992
Aufgabe 1: (5 Punkte)
a) Die Welle 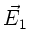 ist linear polarisiert, denn
ist linear polarisiert, denn
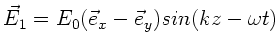 .
.
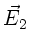 ist zirkular polarisiert, da
ist zirkular polarisiert, da
d.h. der Betrag des 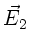 - Feldes verändert sich nicht mit
der Zeit. Den Umlaufsinn ersieht man am einfachsten, indem man den
Vektor an der Stelle
- Feldes verändert sich nicht mit
der Zeit. Den Umlaufsinn ersieht man am einfachsten, indem man den
Vektor an der Stelle 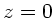 für die Zeiten
für die Zeiten
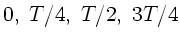 und
und 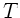 berechnet. Es ist
berechnet. Es ist
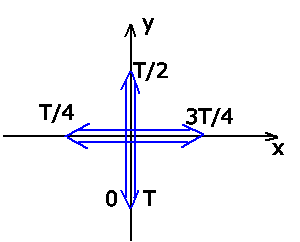
Wie man der folgenden Skizze ansieht, handelt es sich um eine
zirkulare rechtspolarisierte Welle.
b) Nach Vorlesung und den Übungsstunden vom 11.11.92
kann man die Maxwellsche Gleichung
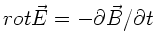 komponentenweise
folgendermaßen schreiben:
komponentenweise
folgendermaßen schreiben:
Dieses ergibt für 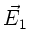 die beiden Gleichungen
die beiden Gleichungen
mit der Lösung (
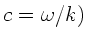 :
:
Entsprechend erhalten wir für 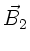 :
:
Aufgabe 2: (5 Punkte)
a) Stromdichte und elektrische Feldstärke sind durch
gegeben. Wir wählen die 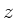 -Achse als Stromrichtung, dann ist
in zylindrischen Koordinaten das
-Achse als Stromrichtung, dann ist
in zylindrischen Koordinaten das  - Feld in positiver
- Feld in positiver
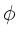 - Richtung gegeben und an der Oberfläche des Leiters (
- Richtung gegeben und an der Oberfläche des Leiters (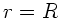 )
betragsmäßig gleich
)
betragsmäßig gleich
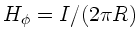 (siehe Physik II).
(siehe Physik II).
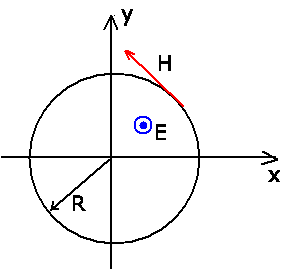
Der Poynting- Vektor ist auf der Oberfläche des
Leiters
also normal auf der Leiteroberfläche in den Leiter hineingerichtet.
Betragsmäßig ist:
a) Die Wärmeleistung des Stromes kann geschrieben werden als:
wobei wir die Integration über das Volumen eines Leiterelementes
der Länge 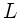 erstreckt haben. Die Integration des Poynting- Vektors über die
Oberfläche (Mantelfläche) des Leiters mit der Länge
erstreckt haben. Die Integration des Poynting- Vektors über die
Oberfläche (Mantelfläche) des Leiters mit der Länge 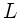 ist entsprechend:
ist entsprechend:
was offensichtlich mit dem vorherigen Ausdruck betragmäßig
identisch ist.
Zahlenwerte: Für die Wärmeleistung folgt pro Meter:
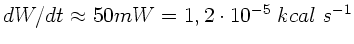 .
c) Die allgemeine Interpretation dieses Beispiel ist wie folgt:
Auf Grund des Poyntingschen Satzes kann die in Form von Wärme dem
elektromagnetischen Feld entzogene Energie nur durch eine einlaufende
Strahlung kompensiert werden. Diese Energiestrahlung erfolgt auf
Grund unseres Ergebnisses radial in den Leiter hinein. Der metallische
Leiter ist hiernach nur in bezug auf den elektrischen Strom als Leiter
anzusehen. Für die Energie ist der Kupferstab dagegen ein nichtleitendes
Medium. Diese wird über das den Zylinder umgebene Vakuum in Form
von Strahlung zugeführt. Das Vakuum stellt bezüglich der Energie
einen Leiter, bezüglich des elektrischen Stromes dagegen einen
Nichtleiter dar. Alles klar ??
.
c) Die allgemeine Interpretation dieses Beispiel ist wie folgt:
Auf Grund des Poyntingschen Satzes kann die in Form von Wärme dem
elektromagnetischen Feld entzogene Energie nur durch eine einlaufende
Strahlung kompensiert werden. Diese Energiestrahlung erfolgt auf
Grund unseres Ergebnisses radial in den Leiter hinein. Der metallische
Leiter ist hiernach nur in bezug auf den elektrischen Strom als Leiter
anzusehen. Für die Energie ist der Kupferstab dagegen ein nichtleitendes
Medium. Diese wird über das den Zylinder umgebene Vakuum in Form
von Strahlung zugeführt. Das Vakuum stellt bezüglich der Energie
einen Leiter, bezüglich des elektrischen Stromes dagegen einen
Nichtleiter dar. Alles klar ??
Aufgabe 3: (10 Punkte)
a) Wellenkette I.
Nach den Kirchhoffschen Regeln gilt in einem Glied der Kette für
die Spannungen:
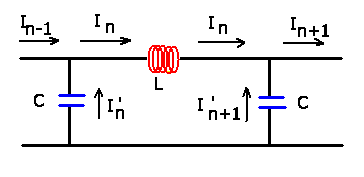
Nochmals nach der Zeit abgeleitet, ergibt die DGL für die Ströme:
Wegen
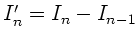 und
und
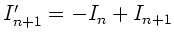 folgt
folgt
Der Strom 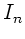 in einem Glied der Kette ist also gekoppelt mit
den Strömem
in einem Glied der Kette ist also gekoppelt mit
den Strömem 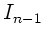 und
und 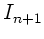 des vorhergehenden und
nachfolgenden Gliedes. Dieses ist völlig equivalent zum System
der durch Federn gekoppelten Massen (siehe Aufgabe 1.4). Als
Lösungsansatz war in der Aufgabenstellung eine harmonische Welle
vorgeschlagen. Dieser Ansatz ist nicht so speziell, wie er auf den
ersten Blick aussehen mag, kann man doch jede periodische Funktion
durch eine Summe von harmonischen Wellen darstellen (Fourier- Analyse).
Da die obige Gleichung linear ist, kann jede allgemeine periodische
Funktion als Lösung aus den harmonischen Wellen aufgebaut werden.
Im übrigen darf die Phasengeschwindigkeit natürlich nicht von der
Form der Welle abhängen.
des vorhergehenden und
nachfolgenden Gliedes. Dieses ist völlig equivalent zum System
der durch Federn gekoppelten Massen (siehe Aufgabe 1.4). Als
Lösungsansatz war in der Aufgabenstellung eine harmonische Welle
vorgeschlagen. Dieser Ansatz ist nicht so speziell, wie er auf den
ersten Blick aussehen mag, kann man doch jede periodische Funktion
durch eine Summe von harmonischen Wellen darstellen (Fourier- Analyse).
Da die obige Gleichung linear ist, kann jede allgemeine periodische
Funktion als Lösung aus den harmonischen Wellen aufgebaut werden.
Im übrigen darf die Phasengeschwindigkeit natürlich nicht von der
Form der Welle abhängen.
Mit dem Lösungsansatz
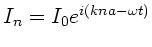 erhalten wir
erhalten wir
Nach Division durch
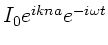 verbleibt:
verbleibt:
Wir bezeichnen die Frequenz der Wellenkette I mit 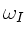 und
die Phasengeschwindigkeit mit
und
die Phasengeschwindigkeit mit 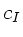 :
:
In diesem Zusammenhang bemerken wir, daß für 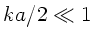 die
Phasengeschwindigkeit des kontinuierlichen Wellenleiters
(siehe Vorlesung Seite 95) herauskommt:
die
Phasengeschwindigkeit des kontinuierlichen Wellenleiters
(siehe Vorlesung Seite 95) herauskommt:
 und
und 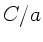 bezeichnet man auch als lineare
Induktivitätsbelegung und lineare Kapazitätsbelegung.
bezeichnet man auch als lineare
Induktivitätsbelegung und lineare Kapazitätsbelegung.
Wellenkette II.

Die Spannung am  -ten Kondensator ist
-ten Kondensator ist
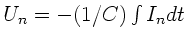 .
Die Bilanz der Spannungen im
.
Die Bilanz der Spannungen im  -ten Glied ist damit
-ten Glied ist damit
Ein zweites Mal differenziert, ergibt die DGL:
Wegen
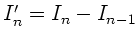 und
und
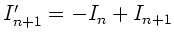 folgt:
folgt:
Wir verwenden wiederum den Ansatz
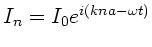 .
Mit einer ähnlichen Rechnung wie bei der Wellenkette I ergibt sich dann:
.
Mit einer ähnlichen Rechnung wie bei der Wellenkette I ergibt sich dann:
Hierbei haben wir die Frequenz und die Phasengeschwindigkeit der
Wellenkette II mit 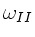 und
und 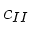 bezeichnet.
bezeichnet.
b) Beide Wellenketten besitzen Grenzfrequenzen, außerhalb derer
die Wellen gedämpft werden. Diesen Sachverhalt erkennt man
folgendermaßen: Falls
so muß
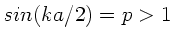 sein. Wie in der Anmerkung zur Aufgabe
erwähnt, ist
sein. Wie in der Anmerkung zur Aufgabe
erwähnt, ist 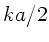 dann aber eine komplexe Zahl:
dann aber eine komplexe Zahl:
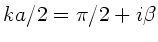 oder
oder
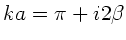 . Setzen wir diese Lösung in die harmonischen
Wellen für die Ströme ein, so gilt
. Setzen wir diese Lösung in die harmonischen
Wellen für die Ströme ein, so gilt
oder, falls wir den Realteil herausprojizieren:
Die Amplitude nimmt also mit wachsendem  schnell ab. Die
Frequenzbereiche, bei denen sich die Wellen ungedämpft fortpflanzen
können, sind daher:
schnell ab. Die
Frequenzbereiche, bei denen sich die Wellen ungedämpft fortpflanzen
können, sind daher:
Man bezeichnet diese Wellenketten daher auch als Hochpaßfilter bzw
Tiefpaßfilter.
c) Die expliziten Ausdrücke für die Ströme im gedämpften Bereich
erhält man mit der angegeben Formel
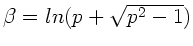 :
:
Mit
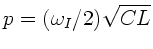 (Wellenkette I) und
(Wellenkette I) und
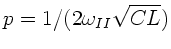 (Wellenkette II) erhalten wir
die Ströme:
(Wellenkette II) erhalten wir
die Ströme:
Harm Fesefeldt
2007-08-22
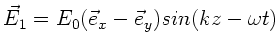 .
.

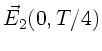
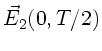
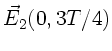
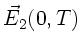

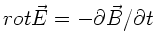 komponentenweise
folgendermaßen schreiben:
komponentenweise
folgendermaßen schreiben:
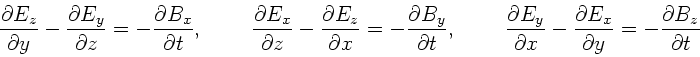
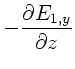
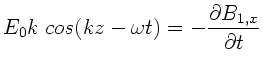
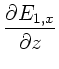
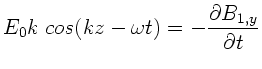
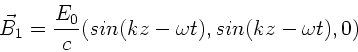
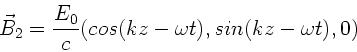
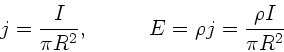


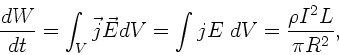


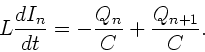
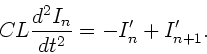
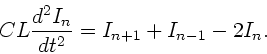
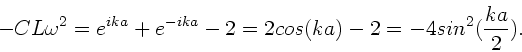
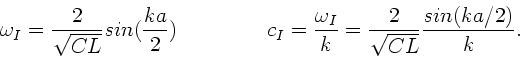
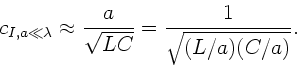

![]() -ten Kondensator ist
-ten Kondensator ist
![]() .
Die Bilanz der Spannungen im
.
Die Bilanz der Spannungen im ![]() -ten Glied ist damit
-ten Glied ist damit