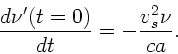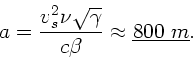Physik III, WS 1992/93
Lösungen zur Übung Nr. 4
Besprechung: 25. November 1992
Aufgabe 1: (10 Punkte)
a) Für den Teil a) dieser Aufgabe gibt es 4 Lösungsmethoden.
Man kann einmal alles im Reellen rechnen, zweitens kann die Feldstärke
komplex und die Fourierkoeffizienten reell angesetzt werden, drittens
kann umgekehrt die Feldstärke reell und die Fourierkoeffizienten
komplex geschrieben werden und letztens können auch beide, die
Feldstärke und die Fourierkoeffizienten komplex angesetzt werden.
Wir werden hier drei von diesen Methoden explizit durchrechnen.
Im folgenden bezeichnen wir die Kreisfrequenz der Grundschwingung
mit
 .
Die folgende Skizze gibt ein Bild des zu untersuchenden Signals
.
Die folgende Skizze gibt ein Bild des zu untersuchenden Signals

Methode 1:
Wir schreiben die Fourierkoeffizienten in der üblichen Form:
Dann kann man  schreiben als:
schreiben als:
Da  für
für
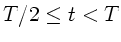 , folgt
, folgt
Wir benutzen die Integralformel
![\begin{displaymath}
\int_{0}^{T/2} e^{-\delta t} cos(bt) dt
= \left[ \frac{e^...
...os(bt))
\right]^{T/2}_{0} = \frac{\delta}{\delta^{2}+b^{2}}.
\end{displaymath}](img8.gif) |
(1) |
Im letzten Schritt wurde ausgenutzt, daß
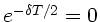 gesetzt
werden kann und damit der Beitrag der oberen Grenze zum Integral
verschwindet. Daher (mit
gesetzt
werden kann und damit der Beitrag der oberen Grenze zum Integral
verschwindet. Daher (mit 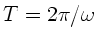 ):
):
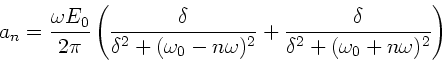 |
(2) |
Dasselbe kann für die Koeffizienten 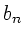 durchgerechnet werden.
Man erhält:
durchgerechnet werden.
Man erhält:
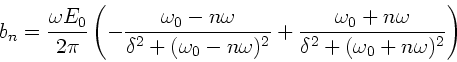 |
(3) |
Methode 2.
Bei der zweiten Methode setzen wir die Fourierkoeffizienten komplex an
und nehmen die Feldstärke weiterhin reell. Dieses Verfahren
wurde ebenfalls in der Vorlesung diskutiert.
Auch hier ist die Berechnung der Koeffizienten relativ einfach und ergibt
Wiederum verschwindet der Beitrag der oberen Grenze zum Integral,
daher ist
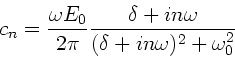 |
(4) |
Falls man in dieser Methode
 gesetzt
hat, erhält man auch
gesetzt
hat, erhält man auch
![\begin{displaymath}
c_{n} = \frac{\omega E_{0}}{4 \pi} \left[ \left(
\frac{\d...
...omega}{\delta^{2}+(\omega_{0}+n\omega)^{2}}
\right) \right].
\end{displaymath}](img21.gif) |
(5) |
Die Koeffizienten 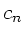 können, müssen aber nicht (siehe Teil b)),
in die Koeffizienten
können, müssen aber nicht (siehe Teil b)),
in die Koeffizienten 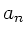 und
und
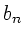 umgerechnet werden. Hierzu benutzen wir die in der Vorlesung
angegebene Formel
umgerechnet werden. Hierzu benutzen wir die in der Vorlesung
angegebene Formel
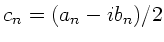 .
Die komplex konjugierte Zahl hierzu ist
.
Die komplex konjugierte Zahl hierzu ist
 . Hieraus folgt, daß
. Hieraus folgt, daß
Methode 3:
Bei der letzten Methode, die wir diskutieren wollen, benutzen wir
die komplexe Darstellung der Fourierkoeffizienten und setzen die
Feldstärke als Realteil der komplexen Funktion
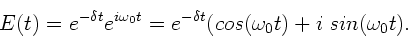 |
(6) |
Wir schreiben
und erinnern daran, daß die Fourierkoeffizienten 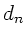 verschieden
von den Koeffizienten
verschieden
von den Koeffizienten 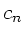 der Methode 2 sind.
Die Berechnung der Fourierkoeffizienten ist jetzt besonders
einfach:
der Methode 2 sind.
Die Berechnung der Fourierkoeffizienten ist jetzt besonders
einfach:
![\begin{displaymath}
d_{n} = \frac{E_{0}}{T} \int_{0}^{T/2}
e^{i(\omega_{0}-n\...
...delta)t}}
{i(\omega_{0}-n\omega+i\delta)} \right]^{T/2}_{0}.
\end{displaymath}](img30.gif) |
(7) |
Wegen
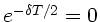 verschwindet wiederum der Beitrag der
oberen Grenze, daher
verschwindet wiederum der Beitrag der
oberen Grenze, daher
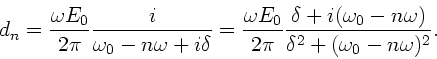 |
(8) |
Bei der letzten Umformung haben wir Zähler und Nenner mit dem
konjugiert Komplexen des Nenners erweitert.
In diesem Fall wollen wir zur Übung die
Koeffizienten 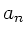 und
und 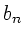 zurückrechnen.
Für das komplexe Feld erhalten wir
zurückrechnen.
Für das komplexe Feld erhalten wir
 |
(9) |
Für den Realteil ergibt sich (man beachte nochmal, daß wir bei
dieser Methode das elektrische Feld als Realteil einer komplexen
Funktion angesetzt haben):
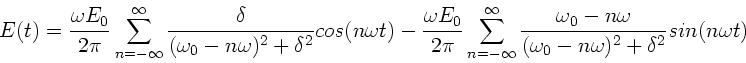 |
(10) |
Der Index 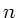 läuft immer noch von
läuft immer noch von 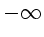 nach
nach 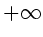 . Mit
. Mit
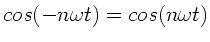 und
und
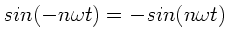 folgt aber sofort
folgt aber sofort
Man identifiziert sofort die 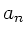 und
und 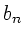 von Methode 1.:
von Methode 1.:
Diese Methode 3 haben wir in die Musterlösung aufgenommen,
da sie in der professionellen Literatur üblich ist.
mm
b) Wir haben also mit drei verschiedenen Methoden drei verschiedene
Sätze von Fourierkoeffizienten erhalten. Dieses zeigt schon, daß die
Fourierkoeffizienten selbst nur mathematische Größen sind.
Die physikalisch interessanten Größen sind die Amplituden und Phasen
der Oberschwingungen.
Während Teil a) dieser Aufgabe reine Mathematik war, wollen wir in Teil b)
und c) die physikalischen Aspekte dieser Aufgabe herausarbeiten.
Jeder physikalisch vorgebildete Mensch wird natürlich davon ausgehen,
daß die Amplitude ungefähr bei der Frequenz 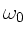 des emittierten
Lichtes maximal wird. Insofern ist die Antwort auf die Frage b) fast
trivial. Wer dieses allerdings nicht erkannt hat, hat die ganze Aufgabe
nicht verstanden.
Das Problem ist die Begründung aus den in Teil a) erhaltenen
Fourierkoeffizienten.
Zur Diskussion der Amplituden muß die Fourierreihe zunächst in
die Form
des emittierten
Lichtes maximal wird. Insofern ist die Antwort auf die Frage b) fast
trivial. Wer dieses allerdings nicht erkannt hat, hat die ganze Aufgabe
nicht verstanden.
Das Problem ist die Begründung aus den in Teil a) erhaltenen
Fourierkoeffizienten.
Zur Diskussion der Amplituden muß die Fourierreihe zunächst in
die Form
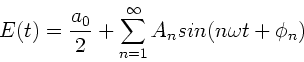 |
(11) |
umgeschrieben werden. Die 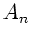 sind die Amplituden, die
sind die Amplituden, die 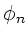 die Phasen der Oberschwingungen. Es gibt durchaus physikalische Probleme,
bei denen auch die Phasen interessant sind, im allgemeinen beschränkt
man die Untersuchung aber auf die Amplituden. Nach Vorlesung gilt
(
die Phasen der Oberschwingungen. Es gibt durchaus physikalische Probleme,
bei denen auch die Phasen interessant sind, im allgemeinen beschränkt
man die Untersuchung aber auf die Amplituden. Nach Vorlesung gilt
(
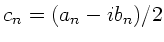 ):
):
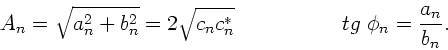 |
(12) |
Wer die 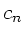 Koeffizienten ausgerechnet hat, kann sofort einen
geschlossenen Ausdruck für die Amplitude hinschreiben:
Koeffizienten ausgerechnet hat, kann sofort einen
geschlossenen Ausdruck für die Amplitude hinschreiben:
Dasselbe Ergebnis erhält man mit den Koeffizienten 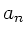 und
und
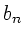 , allerdings nach einer etwas längeren Rechnung.
Die Extremalbedingung
, allerdings nach einer etwas längeren Rechnung.
Die Extremalbedingung
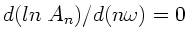 führt nach
kurzer Rechnung tatsächlich auf die Lösung
führt nach
kurzer Rechnung tatsächlich auf die Lösung
Das Aufsuchen des Maximums durch eine Extremalbedingung ist
bei der Methode 1 (
 )
ausgesprochen mühsam und auch nicht notwendig. Zunächst
bemerken wir, daß der Dämpfungsparameter
)
ausgesprochen mühsam und auch nicht notwendig. Zunächst
bemerken wir, daß der Dämpfungsparameter
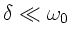 .
In dieser Approximation gilt z.B. für die Koeffizienten
.
In dieser Approximation gilt z.B. für die Koeffizienten 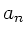 und
und 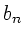 außerhalb des Maximums:
außerhalb des Maximums:
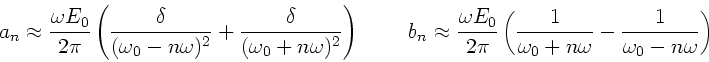 |
(13) |
Ersichtlich gehen die Beträge der Fourierkoeffizienten und damit auch
die Amplitude in dieser Approximation für
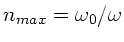 gegen Unendlich. Der Dämpfungsparameter sorgt lediglich dafür,
daß die Amplitude im Maximum endlich bleibt.
Zur genaueren Bestimmung berechnen wir zunächst die
gegen Unendlich. Der Dämpfungsparameter sorgt lediglich dafür,
daß die Amplitude im Maximum endlich bleibt.
Zur genaueren Bestimmung berechnen wir zunächst die 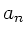 - und
- und
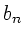 - Koeffizienten im Maximum. Der
- Koeffizienten im Maximum. Der 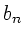 Koeffizient
wechselt bei
Koeffizient
wechselt bei
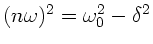 das
Vorzeichen, ist bei diesem Wert selbst also Null. Da aber
das
Vorzeichen, ist bei diesem Wert selbst also Null. Da aber
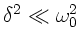 , kann der
, kann der 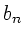 Koeffizient
im Maximum vernachlässigt werden. Numerisch erhalten wir
für
Koeffizient
im Maximum vernachlässigt werden. Numerisch erhalten wir
für
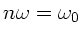 :
:
Für
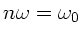 ist daher
ist daher
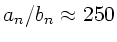 .
Im Ausdruck für
.
Im Ausdruck für 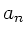 selbst ist im
Maximum der zweite Summand vernachlässigbar klein gegen den ersten
Summanden:
selbst ist im
Maximum der zweite Summand vernachlässigbar klein gegen den ersten
Summanden:
sodaß wir in der Nähe des Maximums einfach setzen können:
Dieser Ausdruck ist aber ersichtlich für
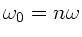 maximal.
Wer es ganz genau wissen will, dem bleibt allerdings nichts anderes
übrig, als einige
Werte um dieses Maximum herum numerisch zu berechnen. Die folgende Tabelle
zeigt Werte für
maximal.
Wer es ganz genau wissen will, dem bleibt allerdings nichts anderes
übrig, als einige
Werte um dieses Maximum herum numerisch zu berechnen. Die folgende Tabelle
zeigt Werte für 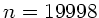 bis
bis 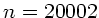 .
.
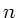 |
19998 |
19999 |
20000 |
20001 |
20002 |
 |
9,99895 |
9,99979 |
10,00024 |
10,00003 |
9,99995 |
Daher:
c) Zur Anfertigung der Skizze muß die Amplitude an einigen Stützpunkten
berechnet werden. Hierbei spielt es keine große Rolle, ob man die
exakten Formeln für die Amplituden oder die Approximationen für
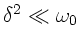 benutzt. Es war ausdrücklich nur eine
Skizze verlangt.
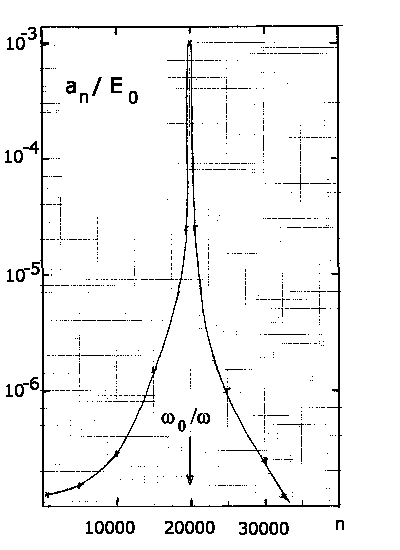
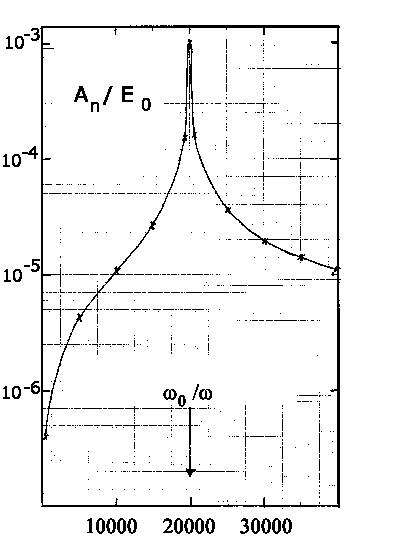
Die folgenden Figuren zeigen
benutzt. Es war ausdrücklich nur eine
Skizze verlangt.
Die folgenden Figuren zeigen 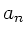 ,
, 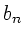 ,
, 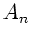 .
Bemerkenswert ist, daß außerhalb der Resonanz die
.
Bemerkenswert ist, daß außerhalb der Resonanz die
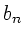 überwiegen, während im Maximum der
überwiegen, während im Maximum der 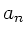 Term absolut
dominiert. Man beachte, daß die Ordinaten eine logarithmische Skala haben.
Term absolut
dominiert. Man beachte, daß die Ordinaten eine logarithmische Skala haben.
Die hier durchgerechnete Aufgabe ist das elektromagnetische Modell
der Stoßverbreiterung von Spektrallinien. Dieses Phänomen
spielt eine herausragende Rolle in der gesamten Atomphysik und
wird in Physik IV sicher noch einmal mit den Methoden der Quantenmechanik
behandelt.

Aufgabe 2: (5 Punkte)
Wir gehen von der in der Vorlesung angegebenen Formel aus:
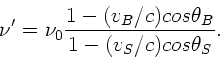 |
(14) |
Wir bezeichnen die Geschwindigkeit der Fledermaus 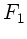 im folgenden
mit
im folgenden
mit
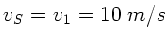 und ihre Senderfrequenz mit
und ihre Senderfrequenz mit
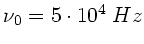 . Betrachten wir zunächst die
Fledermaus
. Betrachten wir zunächst die
Fledermaus 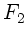 . Diese bewegt sich nicht, also
. Diese bewegt sich nicht, also 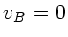 .
Sie hört einmal die direkt von
.
Sie hört einmal die direkt von 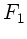 kommenden Frequenzen.
Diese sind wegen
kommenden Frequenzen.
Diese sind wegen
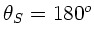 und damit
und damit
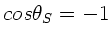 durch
durch
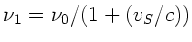 gegeben.
Die Wand wirkt als Empfänger der Welle der Frequenz
gegeben.
Die Wand wirkt als Empfänger der Welle der Frequenz
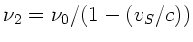 . In diesem Fall ist ebenfalls
. In diesem Fall ist ebenfalls
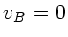 , aber
, aber 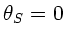 und damit
und damit
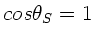 .
Diese Wellen werden reflektiert und ebenfalls von
.
Diese Wellen werden reflektiert und ebenfalls von 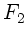 empfangen.
empfangen.
Die Fledermaus 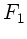 hört einmal die Frequenz
hört einmal die Frequenz 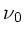 in ihrem
eigenen Ruhesystem. Wie oben schon gesagt, ist die Wand ein
Schallsender der Frequenz
in ihrem
eigenen Ruhesystem. Wie oben schon gesagt, ist die Wand ein
Schallsender der Frequenz  . Relativ zu diesem Sender bewegt
sich
. Relativ zu diesem Sender bewegt
sich 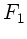 mit der Geschwindigkeit
mit der Geschwindigkeit 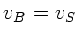 und
und
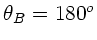 bzw
bzw
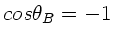 , somit
, somit
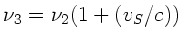 .
.
Zusammenfassung:
Aufgabe 3: (5 Punkte)
Die Situation ist in der folgende Skizze dargestellt.  ist der
ruhende Beobachter,
ist der
ruhende Beobachter,  der Dampfer.
der Dampfer.
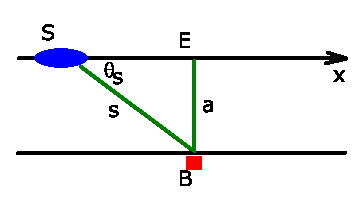
Die in der Vorlesung angegebene Formel für die am Ort 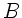 ankommenden
Frequenzen ist
ankommenden
Frequenzen ist
Im folgenden bezeichnen wir die ausgesandte Frequenz mit  , die
beim Beobachter ankommende wahre Frequenz mit
, die
beim Beobachter ankommende wahre Frequenz mit 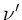 und die vom
Beobachter gemessene Frequenz mit
und die vom
Beobachter gemessene Frequenz mit 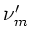 .
Für
.
Für
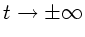 kann
kann
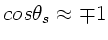 gesetzt werden,
sodaß
gesetzt werden,
sodaß
Aus der Parametrisierung der experimentellen Messungen
folgt für die Frequenzen bei
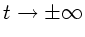 :
:
Setzen wir
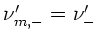 und
und
 , so erhalten
wir zwei Bestimmungsgleichungen für
, so erhalten
wir zwei Bestimmungsgleichungen für  und
und 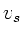 :
:
die gelöst werden durch:
Auf Grund dieser Parametrisierung erhält man eine Geschwindigkeit
und Frequenz, die etwas kleiner als die wirkliche Geschwindigkeit
von 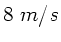 und Frequenz
und Frequenz 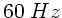 ist. Dieses liegt daran, daß
der Beobachter eine approximative,
und daher nicht ganz korrekte Parametrisierung verwendet hat
(siehe unten).
ist. Dieses liegt daran, daß
der Beobachter eine approximative,
und daher nicht ganz korrekte Parametrisierung verwendet hat
(siehe unten).
Zunächst muß festgestellt werden, daß der Beobachter die Zeitachse
so gelegt hat, daß der Nullpunkt beim minimalen Abstand des
Dampfers vom Beobachter liegt, also bei Punkt  der obigen Skizze.
Denn für
der obigen Skizze.
Denn für 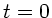 ist
ist
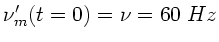 . Daß die gemessenen Frequenzen
für alle anderen Zeiten symmetrisch sind
(
. Daß die gemessenen Frequenzen
für alle anderen Zeiten symmetrisch sind
(
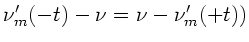 , liegt an der Tatsache,
daß
, liegt an der Tatsache,
daß  und daher
und daher
Diese Approximation stimmt umso besser, je kleiner
 wird, d.h. je mehr sich der Dampfer dem Punkt
wird, d.h. je mehr sich der Dampfer dem Punkt  nähert.
Mit
nähert.
Mit
 und
und
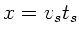 folgt:
folgt:
Man beachte auch, daß die Zeit 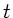 des Beobachters und die Zeit
des Beobachters und die Zeit  des Dampfers nur am Punkt
des Dampfers nur am Punkt  exakt übereinstimmen. Für weitere
Entfernungen ergibt sich auf Grund der endlichen Schallausbreitung
eine Differenz. Dieser Unterschied ist aber wegen
exakt übereinstimmen. Für weitere
Entfernungen ergibt sich auf Grund der endlichen Schallausbreitung
eine Differenz. Dieser Unterschied ist aber wegen 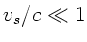 für
für
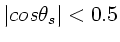 vernachlässigbar klein. Die zeitliche
Änderung der Frequenzen ist für
vernachlässigbar klein. Die zeitliche
Änderung der Frequenzen ist für 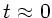 :
:
Aus den Messungen folgt
 ,
daher folgt für den Abstand
,
daher folgt für den Abstand 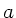 des Dampfers vom Ufer:
des Dampfers vom Ufer:
Man könnte bei der gesamten Lösung dieser Aufgabe natürlich auch
von der Annahme ausgehen, daß bei einem Dampfer grundsätzlich
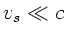 sein muß. Dann kann man von vornherein eine
Taylor- Entwicklung ansetzen und einfach die Parameter vergleichen.
sein muß. Dann kann man von vornherein eine
Taylor- Entwicklung ansetzen und einfach die Parameter vergleichen.
Eine ähnliche Methode wird benutzt, um die Geschwindigkeit und
den Abstand von der Erde bei Satelliten zu messen.
Harm Fesefeldt
2007-08-21



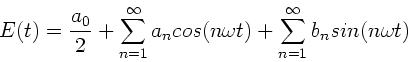
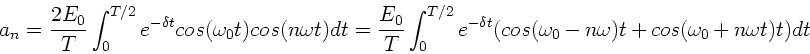
![\begin{displaymath}
\int_{0}^{T/2} e^{-\delta t} cos(bt) dt
= \left[ \frac{e^...
...os(bt))
\right]^{T/2}_{0} = \frac{\delta}{\delta^{2}+b^{2}}.
\end{displaymath}](img8.gif)
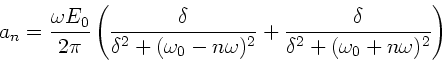
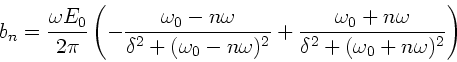

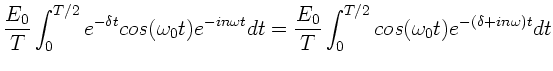
![$\displaystyle \frac{E_{0}}{T} \left[
\frac{e^{-(\delta+in\omega)t}}{(\delta+in\...
...in(\omega_{0}t) - (\delta +in\omega)
cos(\omega_{0}t) \right) \right]^{T/2}_{0}$](img18.gif)
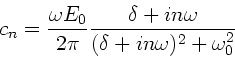
![\begin{displaymath}
c_{n} = \frac{\omega E_{0}}{4 \pi} \left[ \left(
\frac{\d...
...omega}{\delta^{2}+(\omega_{0}+n\omega)^{2}}
\right) \right].
\end{displaymath}](img21.gif)
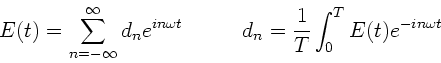
![\begin{displaymath}
d_{n} = \frac{E_{0}}{T} \int_{0}^{T/2}
e^{i(\omega_{0}-n\...
...delta)t}}
{i(\omega_{0}-n\omega+i\delta)} \right]^{T/2}_{0}.
\end{displaymath}](img30.gif)
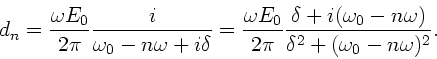

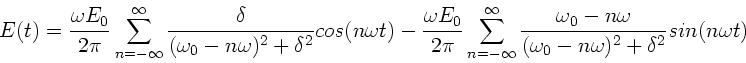

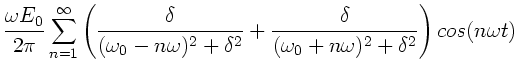
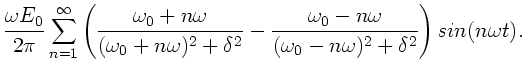
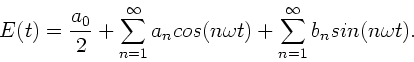
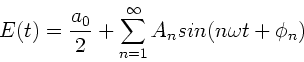
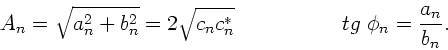
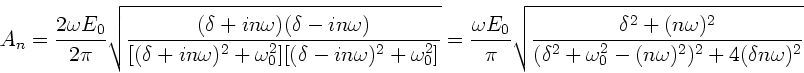
 )
ausgesprochen mühsam und auch nicht notwendig. Zunächst
bemerken wir, daß der Dämpfungsparameter
)
ausgesprochen mühsam und auch nicht notwendig. Zunächst
bemerken wir, daß der Dämpfungsparameter
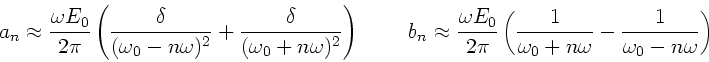
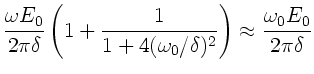

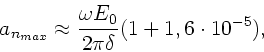
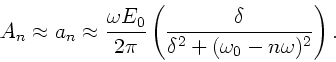
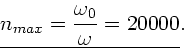



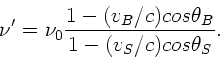
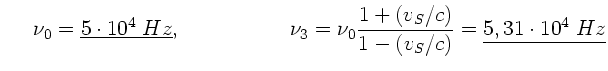


![]() ankommenden
Frequenzen ist
ankommenden
Frequenzen ist
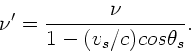

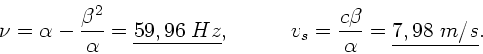
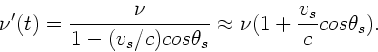
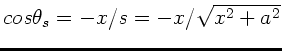 und
und