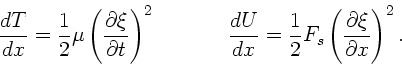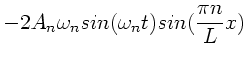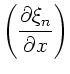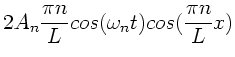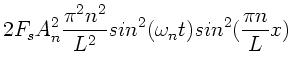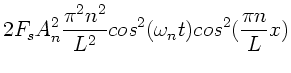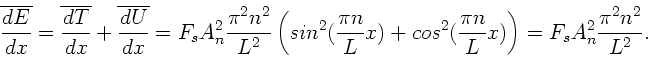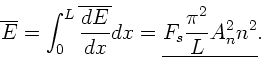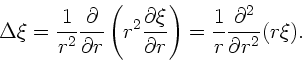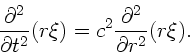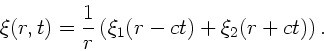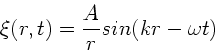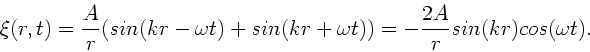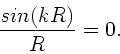Physik III, WS 1992/93
Lösungen zur Übung Nr. 3
Besprechung: 25. November 1992
Aufgabe 1: (5 Punkte)
a) Der Strom  ist gegeben durch
ist gegeben durch
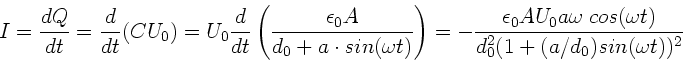 |
(1) |
b) Spezielle Lösung:
Man könnte die Amplituden des Grundtones und des ersten Obertones
mit der Integraldefinition der Fourierkoeffizienten berechnen. Dieses
Vorgehen erweist sich allerdings in diesem Fall bereits als
außerordentlich schwierig. Da nach Hinweis 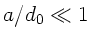 ist,
können wir nach Potenzen von
ist,
können wir nach Potenzen von
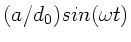 entwickeln. Wegen
entwickeln. Wegen
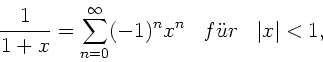 |
(2) |
folgt in zweiter Ordnung von 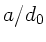 :
:
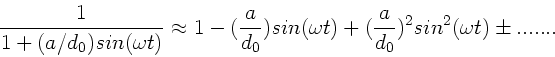 |
(3) |
und
Das Verhältnis der Amplituden ist
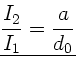 |
(7) |
Die Reihenentwicklung zu dieser Lösung wurde im übrigen in den
Rechenübungen am 4.11.92 auf Seite 3 angegeben.
Allgemeine Lösung:
Die allgemeine Lösung zu dieser Aufgabe wurde ebenfalls in den
Rechenübungen am 4.11.92 diskutiert (Seite 2/3). In der Aufgabe 3
dieser Rechenübungen setzen wir
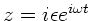 und
entwickeln die Potenzreihe gemäß:
und
entwickeln die Potenzreihe gemäß:
Andererseits erhalten wir für die linke Seite der letzten Gleichung,
wobei wir mit dem konjugiert Komplexen des Nenners erweitern:
Vergleich der Imaginärteile führt auf
Wir setzen
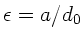 und bemerken, daß nach Aufgabenstellung
und bemerken, daß nach Aufgabenstellung
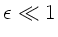 , also erst recht
, also erst recht
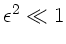 . Daher können
wir im Nenner der linken Seite
. Daher können
wir im Nenner der linken Seite 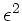 durch
durch
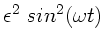 und
und
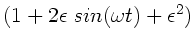 durch
durch
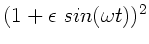 ersetzen. Die Summe auf der
rechten Seite schreiben wir zusätzlich in allgemeiner Form. Dieses
ergibt schließlich für den Strom:
ersetzen. Die Summe auf der
rechten Seite schreiben wir zusätzlich in allgemeiner Form. Dieses
ergibt schließlich für den Strom:
![\begin{displaymath}
I = -\frac{\epsilon_{0} A U_{0} a \omega}{d_{0}^{2}}
\left...
...eft( \frac{a}{d_{0}} \right)^{2n-1} sin(2n\omega t) \right] .
\end{displaymath}](img30.gif) |
(8) |
Für das Verhältnis der Amplituden des 1. Obertones zum Grundton erhält
man das gleiche Ergebnis wie in der obigen speziellen Lösung.
Aufgabe 2: (5 Punkte)
a) Spezielle Lösung
Die Auslenkung und die Steigung des Seils müssen an der
Verbindungsstelle 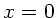 der beiden Seile
der beiden Seile  und
und 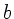 übereinstimmen.
Dieses bedeutet:
übereinstimmen.
Dieses bedeutet:
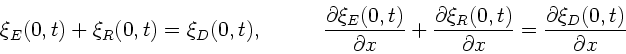 |
(9) |
Setzen wir die angegebenen Wellen ein, so erhält man
oder
 |
(12) |
Aufgelöst nach 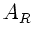 und
und 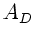 ergibt
ergibt
 |
(13) |
Die Wellenzahlen 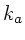 und
und 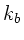 können durch die Dichten
ausgedrückt werden,
können durch die Dichten
ausgedrückt werden,
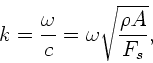 |
(14) |
wobei 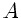 der Querschnitt und
der Querschnitt und 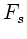 die Spannungskraft bedeutet.
Diese beiden Größen sind für beide Seile gleich groß, daher
die Spannungskraft bedeutet.
Diese beiden Größen sind für beide Seile gleich groß, daher
 |
(15) |
Zahlenwerte eingesetzt:
 |
(16) |
b) Allgemeine Lösung
Der in der Aufgabenstellung gemachte Ansatz für die drei Wellen
schließt schon die Kenntnis der Phasen für die reflektierte und
durchgelassene Welle ein. Allgemeiner hätten wir ansetzen können:
Die Stetigkeitsbedingung
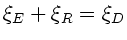 ergibt an der Stelle
ergibt an der Stelle
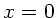 :
:
 |
(20) |
oder:
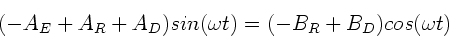 |
(21) |
Da diese Gleichung für alle Zeiten gelten soll, müssen die Koeffizienten
für die Sinusterme und Cosinusterme getrennt gleich Null werden:
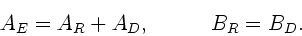 |
(22) |
Aus der zweiten Stetigkeitsbedingung folgern wir entsprechend:
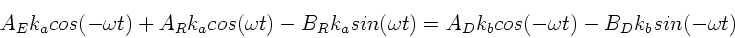 |
(23) |
Wiederum müssen die Koeffizienten der Sinusterme und Cosinusterme
getrennt betrachtet werden, woraus folgt:
 |
(24) |
Die zweite Gleichung kann zusammen mit der oben hergeleiteten
Bedingung 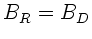 nur erfüllt werden, wenn
nur erfüllt werden, wenn
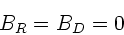 |
(25) |
Unsere Annahme für den einfachen Ansatz der Wellen war also
gerechtfertigt.
Aufgabe 3: (5 Punkte)
Nach Vorlesung ist die Wellenlänge der  -ten Eigenschwingung durch
-ten Eigenschwingung durch
 gegeben, die Kreisfrequenz entsprechend durch
gegeben, die Kreisfrequenz entsprechend durch
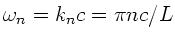 oder auch
oder auch
 mit der linearen
Massendichte
mit der linearen
Massendichte 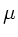 . Nach Übung 2.2 sind die linearen Dichten der
kinetischen und potentiellen Energie:
. Nach Übung 2.2 sind die linearen Dichten der
kinetischen und potentiellen Energie:
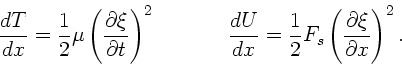 |
(26) |
Aus
folgt
Die zeitliche Mittelung ergibt in beiden Fällen:
 |
(31) |
daher
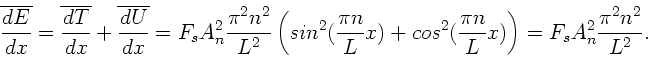 |
(32) |
Als Endergebnis erhalten wir
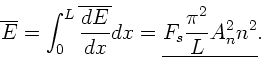 |
(33) |
Die mittlere Energie nimmt also quadratisch mit  zu. Diese gewaltige
Energiezunahme der Obertöne kann nur abgefangen werden, wenn die
Amplitude mit
zu. Diese gewaltige
Energiezunahme der Obertöne kann nur abgefangen werden, wenn die
Amplitude mit
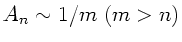 abnimmt. Hieraus kann eine
Nebenbedingung für die Größe der Fourierkoeffizienten hergeleitet
werden.
abnimmt. Hieraus kann eine
Nebenbedingung für die Größe der Fourierkoeffizienten hergeleitet
werden.
Aufgabe 4: (5 Punkte)
Der Laplace Operator 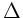 in der allgemeinen dreidimensionalen
Wellengleichung
in der allgemeinen dreidimensionalen
Wellengleichung
 |
(34) |
ist für kugelsymmetrische Probleme durch
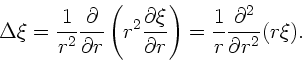 |
(35) |
gegeben. Die Wellengleichung erhält dann die Form:
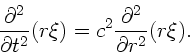 |
(36) |
Die Funktion 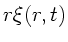 erfüllt also unsere normale Wellengleichung,
hat daher die allgemeine Lösung
erfüllt also unsere normale Wellengleichung,
hat daher die allgemeine Lösung
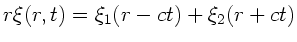 . Dieses kann man auch
schreiben als:
. Dieses kann man auch
schreiben als:
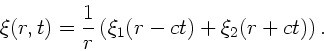 |
(37) |
Die Form der obigen Lösung kann man natürlich durch
Energiebetrachtung einer auslaufenden Kugelwelle erraten.
Spezielle Lösungen sind die auslaufenden harmonischen Kugelwellen
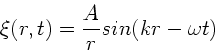 |
(38) |
und die stehenden Kugelwellen
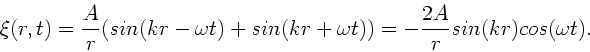 |
(39) |
- Man beachte: Die auslaufenden Wellen
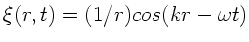 und stehenden Kugelwellen
und stehenden Kugelwellen
 erfüllen zwar auch die
Wellengleichung, sind aber unphysikalisch, da die Amplitude für
erfüllen zwar auch die
Wellengleichung, sind aber unphysikalisch, da die Amplitude für
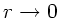 über alle Grenzen wächst, d.h.
über alle Grenzen wächst, d.h.
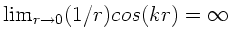 . Im Gegensatz dazu gilt
für die Sinuslösung:
. Im Gegensatz dazu gilt
für die Sinuslösung:
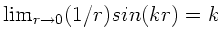 .
.
Als Nebenbedingung müssen wir fordern, daß an den Kugelwänden
keine Luftschwingungen stattfinden, d.h.  :
:
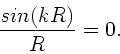 |
(40) |
Diese Bedingung wird erfüllt für alle
 |
(41) |
Mit
 können wir auch schreiben
können wir auch schreiben
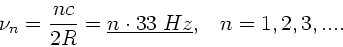 |
(42) |
Harm Fesefeldt
2007-08-21
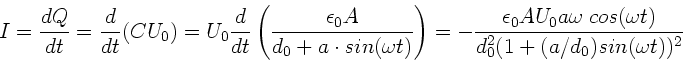
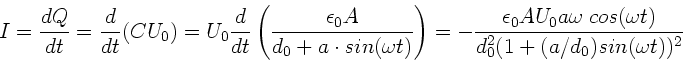
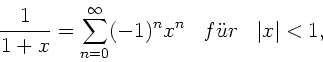
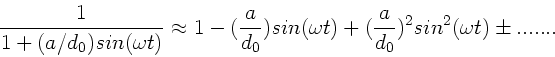
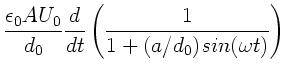
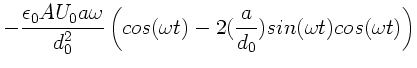
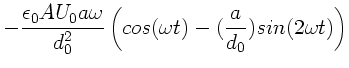
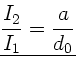
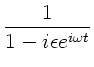
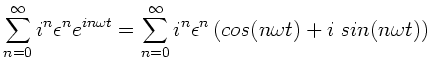

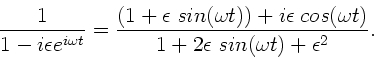
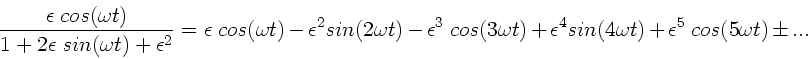
![\begin{displaymath}
I = -\frac{\epsilon_{0} A U_{0} a \omega}{d_{0}^{2}}
\left...
...eft( \frac{a}{d_{0}} \right)^{2n-1} sin(2n\omega t) \right] .
\end{displaymath}](img30.gif)
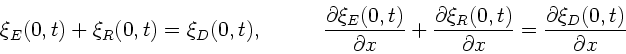

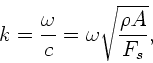


 mit der linearen
Massendichte
mit der linearen
Massendichte