Physik III, WS 1992/93
Lösungen zur Übung Nr. 2
Besprechung: 11. November 1992
Aufgabe 1: (4 Punkte)
Nach Vorlesung kann die Schallgeschwindigkeit in einem Gas durch
ausgedrückt werden. Hierbei ist 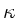 der Adiabatenkoeffizient,
der Adiabatenkoeffizient,
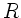 die allgemeine Gaskonstante,
die allgemeine Gaskonstante, 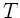 die Temperatur und
die Temperatur und 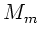 die
Molmasse. Die mittlere quadratische Geschwindigkeit ist (siehe
Physik I)
die
Molmasse. Die mittlere quadratische Geschwindigkeit ist (siehe
Physik I)
Auflösen nach 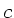 und Einsetzen der Zahlenwerte ergibt
und Einsetzen der Zahlenwerte ergibt
Aufgabe 2: (6 Punkte)
Bei der Schwingung erfährt das Seilstück mit der Länge 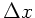 eine
Dehnung
eine
Dehnung
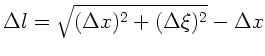 .
.
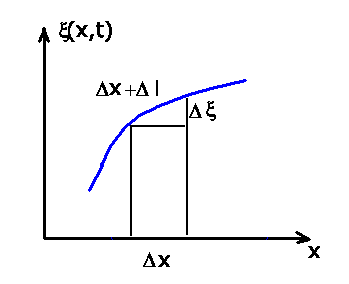
Dieses kann man ausdrücken (siehe Anmerkung zur Aufgabe):
Für
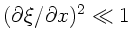 ergibt die Taylorentwicklung
ergibt die Taylorentwicklung
Die potentielle Energie bei der Dehnung ist dann (siehe Hinweis zur
Aufgabe):
also
Die lineare kinetische Energiedichte ist
mit der linearen Massendichte 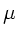 . Da die Welle in positiver
. Da die Welle in positiver
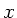 - Richtung laufen soll, gilt
- Richtung laufen soll, gilt
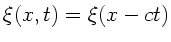 .
Mit
.
Mit 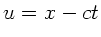 ist dann
ist dann
und
- Man beachte: Dasselbe Ergebnis hätten wir erhalten, wenn
die Welle in negativer
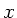 - Richtung läuft. Für die allgemeine
Lösung
- Richtung läuft. Für die allgemeine
Lösung
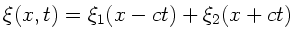 der
Wellengleichung gilt diese Formel dagegen nicht. In diesem Fall erhält
man stattdessen
der
Wellengleichung gilt diese Formel dagegen nicht. In diesem Fall erhält
man stattdessen
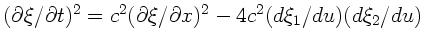 .
.
Diesen obigen Ausdruck setzen wir in die Formel für 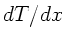 ein und
erhalten
ein und
erhalten
Nach Vorlesungsscript (Seite 13) ist aber
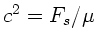 , daher
, daher
Aufgabe 3: (5 Punkte)
Nach Vorlesung ist der Schallpegel (Lautstärke)
Aufgelöst nach 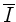 und Einsetzen der Zahlenwerte
und Einsetzen der Zahlenwerte
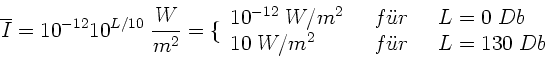 |
(1) |
Nach Vorlesung Seite 27 ist der zeitliche Mittelwert der Intensität
und daher (
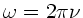 )
)
Für Luft bei 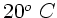 und Normaldruck ist
und Normaldruck ist
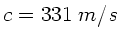 und
und
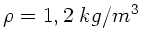 . Zahlenwerte eingesetzt
ergibt
. Zahlenwerte eingesetzt
ergibt
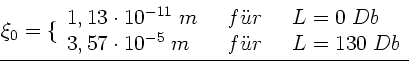 |
(2) |
Aufgabe 4: (5 Punkte)
Nach Vorlesung ist die resultierende Welle zweier harmonischer Wellen
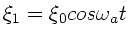 und
und
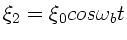 mit dicht nebeneinander liegenden
Frequenzen
mit dicht nebeneinander liegenden
Frequenzen 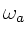 und
und 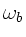 durch
durch
gegeben, mit der modulierten Amplitude 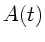 und der mittleren Frequenz
und der mittleren Frequenz 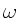 .
Das menschliche Ohr ist ein Empfänger mit quadratischem Gesetz, es
reagiert nicht auf
.
Das menschliche Ohr ist ein Empfänger mit quadratischem Gesetz, es
reagiert nicht auf 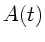 , sondern auf
, sondern auf 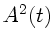 , d.h.
, d.h.
Die wahrgenommenen Kreisfrequenzen der Schwebung sind also
oder für die Frequenzen:
Da die Stimmgabel mit der niedrigsten Frequenz angegeben war (500 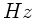 ),
muß die Stimmgabel mit der höchsten Frequenz
),
muß die Stimmgabel mit der höchsten Frequenz 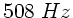 haben.
Für die mittleren Frequenzen gibt es zwei Lösungen.
Nach einigem Probieren findet man:
haben.
Für die mittleren Frequenzen gibt es zwei Lösungen.
Nach einigem Probieren findet man:
mit den Schwebungsfrequenzen
oder
mit den Schwebungsfrequenzen
Harm Fesefeldt
2007-08-21
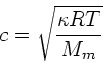
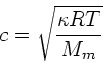
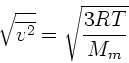
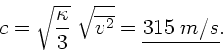
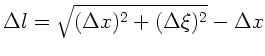 .
.

![\begin{displaymath}
\Delta l = \left[ \sqrt{1+\left(\frac{\partial\xi}{\partial x}\right)^{2}}
-1 \right] \Delta x. \nonumber
\end{displaymath}](img11.gif)
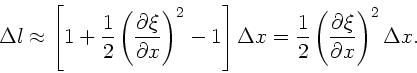
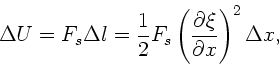
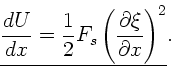
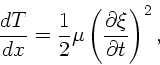
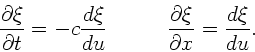
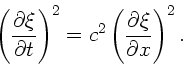
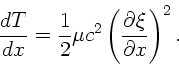
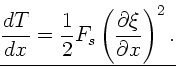
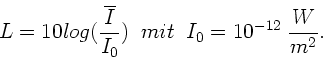
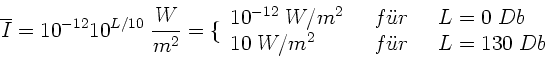
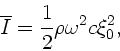
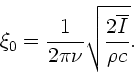
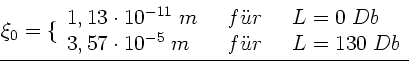
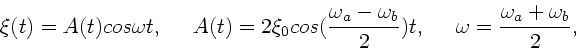
![\begin{displaymath}
A^{2}(t) = 4 \xi_{0}^{2} cos^{2}(\frac{\omega_{a}-\omega_{b}}{2})t
= 2 \xi_{0}^{2} [1 + cos(\omega_{a}-\omega_{b})t ].
\end{displaymath}](img47.gif)