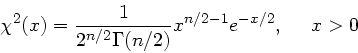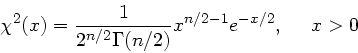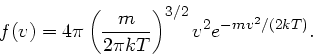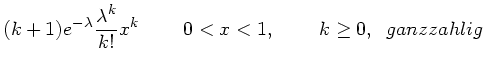12. Übung
Bearbeitung vom 24.01.07 - 29.01.07
Aufgabe 1: Variablentransformation
Die 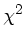 - Verteilung mit
- Verteilung mit 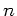 Freiheitsgraden lautete:
Freiheitsgraden lautete:
Zeigen Sie, daß man aus der 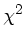 - Verteilung mit 3 Freiheitsgraden mit Hilfe
der Transformnation
- Verteilung mit 3 Freiheitsgraden mit Hilfe
der Transformnation
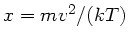 die Maxwellsche Geschwindigkeitsverteilung
von Atomen oder Molekülen in einem idealen Gas erhält (siehe auch Aufgabe 3 im
Übungsblatt Nr.8):
die Maxwellsche Geschwindigkeitsverteilung
von Atomen oder Molekülen in einem idealen Gas erhält (siehe auch Aufgabe 3 im
Übungsblatt Nr.8):
Anmerkung: Für die Gammafunktion gilt:
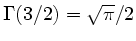 .
.
Aufgabe 2: Zweidimensionale Verteilungen
Im folgenden sind 3 zweidimensionale Wahrscheinlichkeitsdichten angegeben:
a) Bei welchen Verteilungen sind die beiden Variablen korreliert ?
b) Bestimmen Sie die eindimensionalen Randverteilungen (eine unendliche Summe braucht nicht
ausgewertet zu werden).
Anmerkung: Es gilt
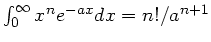 für
für 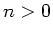 , ganzzahlig.
, ganzzahlig.
Aufgabe 3: Korrelationen
In den 3 Files file1.dat, file2.dat, file3.dat haben wir Stichproben aus
zweidimensionalen Verteilungen mit jeweils 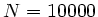 Wertepaaren abgespeichert.
Bestimmen Sie die Korrelationskoeffizienten einschließlich der Fehler.
Tragen Sie die Stichproben in 2-dimensionale Histogramme ein und überprüfen Sie
Ihre Ergebnisse visuell. Vergleichen Sie auch die Randverteilungen der 3 Stichproben
miteinander.
Wertepaaren abgespeichert.
Bestimmen Sie die Korrelationskoeffizienten einschließlich der Fehler.
Tragen Sie die Stichproben in 2-dimensionale Histogramme ein und überprüfen Sie
Ihre Ergebnisse visuell. Vergleichen Sie auch die Randverteilungen der 3 Stichproben
miteinander.
Harm Fesefeldt
2007-01-23