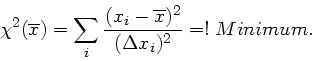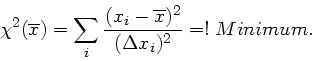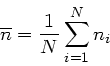11. Übung
Bearbeitung vom 17.01.07 - 22.01.07
Aufgabe 1: Fehlerfortpflanzung
Die Zeit 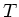 für die Periode der Bewegung eines mathematischen Pendels ist durch
für die Periode der Bewegung eines mathematischen Pendels ist durch
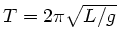 gegeben.
Dabei ist
gegeben.
Dabei ist 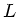 die Länge des Pendels und
die Länge des Pendels und 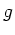 die Erdbeschleunigung. Berechnen Sie
die Erdbeschleunigung. Berechnen Sie 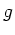 und
und 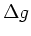 unter
Benutzung der Meßwerte
unter
Benutzung der Meßwerte
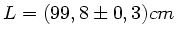 und
und
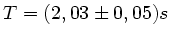 . Nehmen Sie an, daß die Meßwerte
unkorreliert sind.
Aufgabe 2: Gewichtetes Mittel
. Nehmen Sie an, daß die Meßwerte
unkorreliert sind.
Aufgabe 2: Gewichtetes Mittel
a) Beweisen Sie die Formel (38) im Skript Teil 9, Absatz 11.4, für die Berechnung des gewichteten Mittelwertes
mit Hilfe der 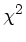 Bedingung
Bedingung
Hierbei werden die 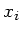 als unabhängige Messungen vorausgesetzt.
als unabhängige Messungen vorausgesetzt.
b) Die Masse des 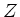 - Bosons ist mittlerweise eine der am genauesten gemessenen Größen der Physik. Das war nicht
immer so. Im Datenfile Z_Mass.dat finden Sie die Messungen verschiedener Experimente. In jeder Zeile ist die
erste Zahl die Jahreszahl der Veröffentlichung, die zweite Zahl die Masse in Einheiten von GeV (
- Bosons ist mittlerweise eine der am genauesten gemessenen Größen der Physik. Das war nicht
immer so. Im Datenfile Z_Mass.dat finden Sie die Messungen verschiedener Experimente. In jeder Zeile ist die
erste Zahl die Jahreszahl der Veröffentlichung, die zweite Zahl die Masse in Einheiten von GeV (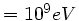 ) und die
letzte Zahl der Fehler der Messung. Berechnen Sie das gewichtete Mittel der
) und die
letzte Zahl der Fehler der Messung. Berechnen Sie das gewichtete Mittel der 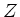 -Masse einschließlich des Fehlers
mit allen bis dahin veröffentlichten Ergebnissen
am Ende des Jahres 1989, am Ende des Jahres 1995 und am Ende des Jahres 2000.
-Masse einschließlich des Fehlers
mit allen bis dahin veröffentlichten Ergebnissen
am Ende des Jahres 1989, am Ende des Jahres 1995 und am Ende des Jahres 2000.
Aufgabe 3: Maximum Likelihood
a) Bei der Poisson- Verteilung gibt es nur einen Parameter 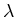 . Zeigen Sie, daß aus der Likelihood- Bedingung
. Zeigen Sie, daß aus der Likelihood- Bedingung
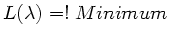 folgt, daß der arithmetische Mittelwert einer unabhängigen Stichprobe
folgt, daß der arithmetische Mittelwert einer unabhängigen Stichprobe
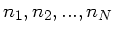
der beste Estimator des Parameters 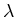 ist.
ist.
b) Im Datenfile Poisson.dat befinden sich die Werte einer Stichprobe aus einer Poisson- Statistik. Bestimmen Sie
hieraus mit Hilfe der Maximum Likelihood Methode den Wert für 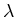 einschließlich des Fehlers.
einschließlich des Fehlers.
Harm Fesefeldt
2007-01-16