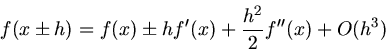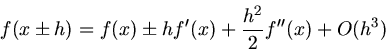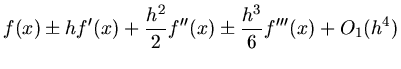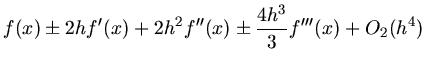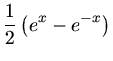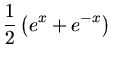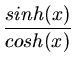4. Übung
Bearbeitung vom 15.11.06 - 20.11.06
Aufgabe 1: Numerische Differentiationen
Wir schreiben die Taylerentwicklung um den Punkt 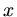 bis zur Ordnung
bis zur Ordnung 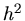 :
:
Hieraus folgt:
Dieses ist die 3- Point Approximation. Wir gehen einen Schritt weiter und schreiben die Taylorentwicklungen
für die Punkte 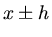 sowie
sowie 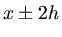 bis zur Ordung
bis zur Ordung 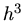 :
:
Daraus berechnen wir (bitte zu Hause nachrechnen!):
Dieses nennt man die 5-Point Approximation.
a) Ersetzen Sie im Programm newton_cos.cc die analytische Berechnung der Ableitung durch ein
numerisches Verfahren mit der 5-Point Approximation.
b) Die Hyperbelfunktionen sind definiert als
Der 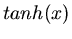 hat eine Nullstelle bei
hat eine Nullstelle bei 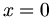 . Die Ableitung ist
. Die Ableitung ist 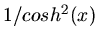 . Sie können die
Funktion graphisch in unserem Funktionsplotter visualisieren. Für welche
Bereiche des Startwertes
. Sie können die
Funktion graphisch in unserem Funktionsplotter visualisieren. Für welche
Bereiche des Startwertes 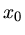 konvergiert das Newton- Verfahren nicht ?
konvergiert das Newton- Verfahren nicht ?
Aufgabe 2: Fourieranalyse
Verändern Sie das Programm test_hebbeker1.cc so, daß es eine Fourierzerlegung der in
hebbeker1.o programmierten Funktion durchführt, und zwar mit 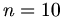 Fourieramplituden
und
Fourieramplituden
und 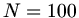 Funktionswerten.
Linken Sie dazu die Object- Datei zusammen mit test_hebbeker1.cc zu einer ausführbaren Datei.
Funktionswerten.
Linken Sie dazu die Object- Datei zusammen mit test_hebbeker1.cc zu einer ausführbaren Datei.
Aufgabe 3: Differentialgleichungen (Zusatzaufgabe für die Oberschlauen)
Mit Hilfe der Ausdrücke (1) und (2) kann man ebenso eine numerische Formel für die zweite Ableitung
herleiten:
Die Funktion
erfüllt mathematisch exakt die Gleichung
Wenn man für die Ableitungen die numerischen 5- Punkt Approximationen einzetzt, erhält man
Untersuchen Sie, wie 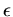 vom Parameter
vom Parameter 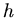 in der Taylor- Entwicklung abhängt.
in der Taylor- Entwicklung abhängt.
Harm Fesefeldt
2006-11-14