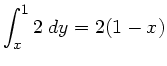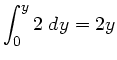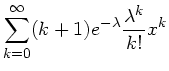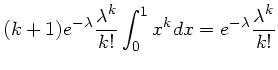Lösungen zur 12. Übung
Bearbeitung vom 24.01.07 - 29.01.07
Aufgabe 1: Variablentransformation
Wegen der Erhaltung der Wahrscheinlichkeit muss
sein, daher
Mit
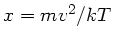 ,
,
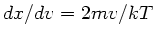 und
und 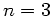 folgt
folgt
Umformung des Ausdrucks und Einsetzen von
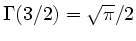 liefert dann
die im Übungsblatt angegebene Formel.
liefert dann
die im Übungsblatt angegebene Formel.
Aufgabe 2: Zweidimensionale Verteilungen
In der ersten Verteilung ist die Wahrscheinlichkeitsdichte nur in einem Dreieck
in der 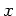 -
-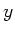 - Ebene von Null verschieden, das durch die Punkte (0,0), (0,1) und (1,1)
definiert ist. Daher sind
- Ebene von Null verschieden, das durch die Punkte (0,0), (0,1) und (1,1)
definiert ist. Daher sind 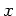 und
und 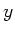 korreliert.
Die Randverteilungen sind:
korreliert.
Die Randverteilungen sind:
Bei der zweiten Verteilung sind die Variablen unkorreliert, da
Hier sind 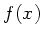 und
und 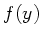 direkt die Randverteilungen.
direkt die Randverteilungen.
In der letzen Verteilung sind 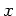 und
und 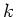 korreliert mit den Randverteilungen
korreliert mit den Randverteilungen
Wegen des Terms 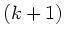 läßt sich die Summe nicht mehr vereinfachen.
läßt sich die Summe nicht mehr vereinfachen.
Aufgabe 3: Korrelationen
Die Stichproben haben alle drei die gleichen Mittelwerte und Varianzen, unterscheiden sich
lediglich im Korrelationskoeffizienten. Im File1 ist 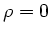 , im File2
ist
, im File2
ist 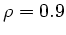 , im File3 ist wiederum
, im File3 ist wiederum 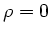 , allerdings ist die Verteilung trotzdem
extrem korreliert (siehe pict1.gif,
pict2.gif und pict3.gif ). Das Analyseprogramm
ist in correlation.C angegeben.
, allerdings ist die Verteilung trotzdem
extrem korreliert (siehe pict1.gif,
pict2.gif und pict3.gif ). Das Analyseprogramm
ist in correlation.C angegeben.
Harm Fesefeldt
2007-01-23
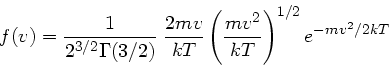
![]() -
-![]() - Ebene von Null verschieden, das durch die Punkte (0,0), (0,1) und (1,1)
definiert ist. Daher sind
- Ebene von Null verschieden, das durch die Punkte (0,0), (0,1) und (1,1)
definiert ist. Daher sind ![]() und
und ![]() korreliert.
Die Randverteilungen sind:
korreliert.
Die Randverteilungen sind: