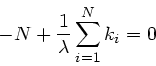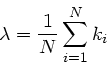11. Übung
Bearbeitung vom 17.01.07 - 22.01.07
Aufgabe 1: Fehlerfortpflanzung
Wir schreiben die Formel um nach
Die partiellen Ableitungen sind
Der quadratische Fehler ist dann
Wir verwenden bei der Angabe nur 2 Stellen des Fehlers, daher
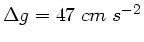 .
Unser gemessenes Ergebnis ist also
.
Unser gemessenes Ergebnis ist also
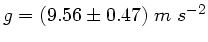 .
.
Aufgabe 2: Gewichtetes Mittel
a) Aus
folgt
Mit den Gewichten
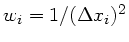 also
also
oder
b) Das Programm Zmass.C bestimmt diese Mittelwerte. Der offizielle Wert in der PDG Tabelle ist allerdings nur
aus den letzten 5 Ergebnissen bestimmt, liegt also etwas höher als der von uns errechnete Wert.
Aufgabe 3: Maximum Likelihood
a) Wir setzen die Formel für die Poisson- Verteilung
in die Likelihood- Formel ein:
Die Ableitung nach 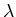 liefert:
liefert:
Daraus folgt
und
b) Im Programm poisson.C bestimmen wir zunächst den Mittelwert. Es ergibt sich zu 2.4.
Theoretisch sollte der symmetrische Fehler durch
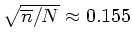 gegeben sein. Aus der
Maximum Likelihood Kurve lesen wir einen Wert von
gegeben sein. Aus der
Maximum Likelihood Kurve lesen wir einen Wert von 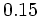 ab. Das Endergebnis ist also:
ab. Das Endergebnis ist also:
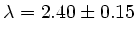 .
.
Harm Fesefeldt
2007-01-16
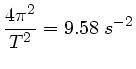
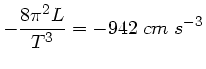
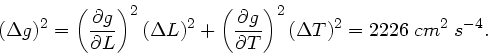
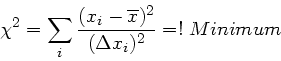
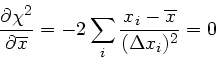
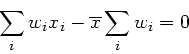
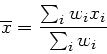
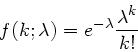
![\begin{displaymath}
L -2 \sum_{i=1}^{N} ln f(k_{i}, \lambda) = -2 \sum_{i=1}^{N} [(-\lambda) + k_{i} ln(\lambda) - ln(k_{i}!)]
\end{displaymath}](img16.gif)
![\begin{displaymath}
\frac{\partial L}{\partial \lambda} = - 2 \sum_{i=1}^{N} [(-1) + \frac{k_{i}}{\lambda}] = 0
\end{displaymath}](img18.gif)