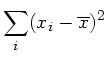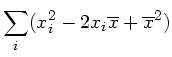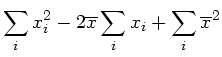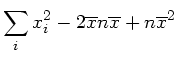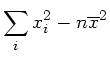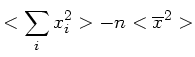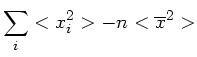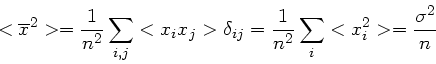10. Übung

Bearbeitung vom 10.01.07 - 15.01.07

Aufgabe 1: Transformationsmethode
Das Integral ist in diesem Fall

$$P(\xi) = \int_{-\infty}^{\xi} \frac{1}{\pi(1+x^{2}} dx = \fr... ...ight]_{-\infty}^{\xi} = \frac{1}{\pi} arctg(\xi) + \frac{1}{2}$$

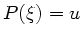Wir würfeln eine Zahl $u \in U[0,1]$ und setzen $P(\xi) = u$. Die Umkehrung ist dann

$$\xi = tan(\pi(u-0.5))$$

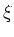$\xi$ ist dann eine Veränderliche aus einer Cauchy- Verteilung. Das Program ist zusammen mit dem Programm von Aufgabe 2 in Cauchy_BreitWigner.C gelistet.
Aufgabe 2: Rückweisungsmethode
Die modifizierte Breit-Wigner Verteilung ist noch nicht auf 1 normiert. Bei Benutzung der Rückweisungsmethode braucht man die Normierung nicht zu kennen, man muß lediglich das Maximum der Funktion bestimmen, damit die Effizienz maximal wird. Das Programm ist in Cauchy_BreitWigner.C enthalten. Die Effizienz ist ca. 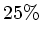$25 \%$.
Aufgabe 3: Stichproben
Wir schreiben

$$(n-1) s^{2} = \sum_{i} (x_{i} - \overline{x})^{2}$$

$$= \sum_{i} (x_{i}^{2} - 2 x_{i} \overline{x} + \overline{x}^{2} )$$

$$= \sum_{i} x_{i}^{2} - 2 \overline{x} \sum_{i} x_{i} + \sum_{i} \overline{x}^{2}$$

$$= \sum_{i} x_{i}^{2} - 2 \overline{x} n \overline{x} + n \overline{x}^{2}$$

$$= \sum_{i} x_{i}^{2} - n \overline{x}^{2}$$

Wir bilden jetzt die Erwartungswerte auf beiden Seiten:

$$< (n-1) s^{2}> = < \sum_{i} x_{i}^{2} > - n < \overline{x}^{2} >$$

$$= \sum_{i} < x_{i}^{2} > - n < \overline{x}^{2} >$$

$$= n \sigma^{2} -n < \overline{x}^{2} >$$

Der rechts stehende Ausdruck ist

$$< \overline{x}^{2} > = \frac{1}{n^{2}} \sum_{i,j} <x_{i} x_{... ... \frac{1}{n^{2}} \sum_{i} < x_{i}^{2} > = \frac{\sigma^{2}}{n}$$

Eingesetzt in den obigen Ausdruck folgt

$$<(n-1) s^{2} > = n \sigma^{2} - \sigma^{2} = (n-1) \sigma^{2}$$

oder eben $< s^{2} > = \sigma^{2}$.
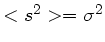Aufgabe 4: Nochmal eine Stichprobe (Zusatzaufgabe)
Für große Werte von 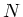$N$ erhält man natürlich perfekte Übereinstimmung von 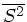$\overline{S^{2}}$ mit dem 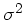$\sigma^{2}$ von Aufgabe 2. Für kleine Werte von 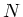$N$ ist die Übereinstimmung nicht ganz so gut (???). Das Programm ist in Average.C gelistet.