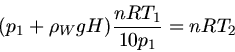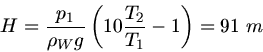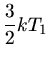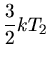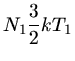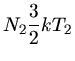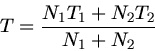Übung Nr.11
Besprechung: Donnerstag, d. 19. Januar 2006
Aufgabe 1:
Für eine Längenänderung 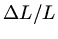 benötigt man eine Kraft (siehe Skript
benötigt man eine Kraft (siehe Skript
mit dem Elastizitätsmodul 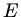 und Querschnitt
und Querschnitt 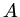 . In unserem Fall wirkt keine Kraft von außen, sondern das
Seil möchte sich durch eine Erniedrigung
. In unserem Fall wirkt keine Kraft von außen, sondern das
Seil möchte sich durch eine Erniedrigung 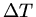 der Temperatur verkürzen:
der Temperatur verkürzen:
Da die Länge des Seils konstant bleibt, wird die Kraft (Spannung) im Seil erhöht:
Zusammen mit der Vorspannung 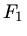 erhalten wir die Gesamtkraft:
erhalten wir die Gesamtkraft:
Man muß also immer darauf gefaßt sein, daß Seile, die man im Sommer gespannt hat, im Winter reißen.
Aufgabe 2:
Die Anomalie des Wassers sorgt dafür, daß unterhalb einer gewissen Oberfläche des Wassers die Temperatur 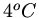 beträgt. Bei dieser Temperatur ist die Dichte am größten, sodaß das Wasser dieser Temperatur nach unten absinkt.
Dieses gilt nicht nur für Temperaturen kleiner als
beträgt. Bei dieser Temperatur ist die Dichte am größten, sodaß das Wasser dieser Temperatur nach unten absinkt.
Dieses gilt nicht nur für Temperaturen kleiner als 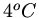 (Eis), sondern auch für höhere Temperaturen.
Die Temperatur ist also nicht nur am Boden des Sees
(Eis), sondern auch für höhere Temperaturen.
Die Temperatur ist also nicht nur am Boden des Sees 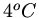 , sondern bis auf eine relativ kleine Schicht an der Oberfläche
im gesamten See. Weiterhin wurde in der Aufgabe angegeben, daß die Luftblase langsam aufsteigen soll. Dann findet nämlich
immer ein Temperaturausgleich zwischen dem Wasser und der Luft der Blase statt. Die Luftblase hat also die gleiche Temperatur
wie das Wasser.
, sondern bis auf eine relativ kleine Schicht an der Oberfläche
im gesamten See. Weiterhin wurde in der Aufgabe angegeben, daß die Luftblase langsam aufsteigen soll. Dann findet nämlich
immer ein Temperaturausgleich zwischen dem Wasser und der Luft der Blase statt. Die Luftblase hat also die gleiche Temperatur
wie das Wasser.
An der Oberfläche gilt dann
mit
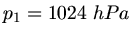 äußerer Luftdruck,
äußerer Luftdruck,
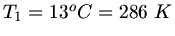 Temperatur.
In der Tiefe
Temperatur.
In der Tiefe 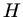 gilt:
gilt:
mit
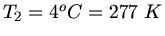 . Nach Aufgabenstellung sollte
. Nach Aufgabenstellung sollte
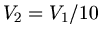 sein, der Druck
sein, der Druck 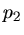 ist
ist
Eingesetzt in die Gleichung folgt:
Das Volumen 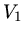 holen wir uns aus der ersten Gleichung
holen wir uns aus der ersten Gleichung
Aufgelöst nach 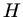 folgt:
folgt:
Aufgabe 3:
Leistung ist Energie pro Zeit, d.h.
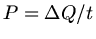 . Die Energie, die der Tauchsieder abgibt,
wird in die Erwärmung des Wassers und in die Erwärmung des Gefäßes hineingesteckt:
. Die Energie, die der Tauchsieder abgibt,
wird in die Erwärmung des Wassers und in die Erwärmung des Gefäßes hineingesteckt:
mit 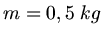 ,
,
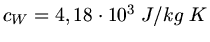 (siehe Skript),
(siehe Skript),
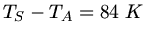 und
und
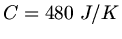 . Die Zeit ist dann:
. Die Zeit ist dann:
Zusatzfrage: Sie vergessen, den Tauchsieder abzustellen. Nach welcher Zeit nach dem Beginn des Kochens ist das
gesamte Wasser verdampft ?
Lösung: Hier ist die Energie
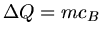 mit wiederum
mit wiederum 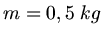 , jetzt aber die Verdampfungswärme
, jetzt aber die Verdampfungswärme
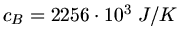 (siehe Skript). Da wir die Temperatur nicht mehr erhöhen, braucht die Wärmekapazität des
Gefäßes nicht mehr berücksichtigt zu werden. Die Zeit ist dann
(siehe Skript). Da wir die Temperatur nicht mehr erhöhen, braucht die Wärmekapazität des
Gefäßes nicht mehr berücksichtigt zu werden. Die Zeit ist dann
Nach dieser Zeit wird es brenzlig, da können Sie schon mal die Feuerwehr rufen.
Online-Aufgabe:
In der Online- Aufgabe war nach der Mischungstemperatur zweier idealer Gase gefragt. Die mittlere kinetischen
Energien der einzelnen Gasatome sind:
Die Gesamtenergien in den beiden Gasen sind also:
Nach der Mischung muss die Summe der Gesamtenergien der Einzelgase gleich der Gesamtenergie des vermischten Gases sein:
Daraus folgt die Mischungstemperatur
Mit 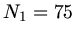 ,
, 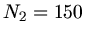 ,
,
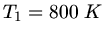 und
und
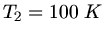 folgt
folgt
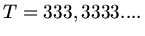 .
In der Animation beobachtet man einen etwas anderen Wert. Dies liegt daran, daß wir in der Rechnung die Atome als
punktförmig angenommen haben. Dieses kann man in der Animation nicht machen, da die Teilchen dann keine
Stossprozesse mehr machen würden. Man müsste theoretisch die van der Waalsche Zustandsgleichung anwenden, bei der die
endliche Ausdehnung der Atome berücksichtigt wird.
.
In der Animation beobachtet man einen etwas anderen Wert. Dies liegt daran, daß wir in der Rechnung die Atome als
punktförmig angenommen haben. Dieses kann man in der Animation nicht machen, da die Teilchen dann keine
Stossprozesse mehr machen würden. Man müsste theoretisch die van der Waalsche Zustandsgleichung anwenden, bei der die
endliche Ausdehnung der Atome berücksichtigt wird.
Frage: Was passiert in der Animation, wenn die Masse der Teilchen verändert wird ?
Frage: Was passiert in der Animation, wenn der Radius der Teilchen verändert wird ?
Harm Fesefeldt
2006-01-23