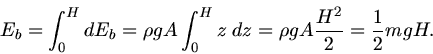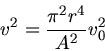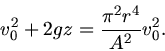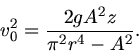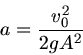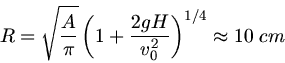Lösungen zur Übung Nr.10
Besprechung: Donnerstag, d. 12. Januar 2006
Aufgabe 1:
Im ersten Fall muß die gesamte Wassermnge 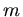 auf die Höhe
auf die Höhe 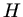 gebracht werden. Energieerhaltung verlangt hier
einfach
gebracht werden. Energieerhaltung verlangt hier
einfach 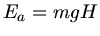 . Im zweiten Fall beträgt die Energie zum Anheben der Wasseroberfläche um den Betrag
. Im zweiten Fall beträgt die Energie zum Anheben der Wasseroberfläche um den Betrag 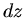 :
:
Hierbei ist 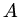 Bodenfläche des Tanks,
Bodenfläche des Tanks, 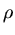 die Dichte des Wassers und
die Dichte des Wassers und 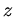 die Höhe des Wasserspiegels. Die Integration liefert
die Höhe des Wasserspiegels. Die Integration liefert
Also ist
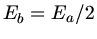 , man benötigt im zweiten Fall also nur halb so viel Energie. Dieses Ergebnis ist plausibel,
da die potentielle Energie im ersten Fall beim Herunterfallen des Wassers verloren geht b.z.w. in Wärme verwandelt
wird.
, man benötigt im zweiten Fall also nur halb so viel Energie. Dieses Ergebnis ist plausibel,
da die potentielle Energie im ersten Fall beim Herunterfallen des Wassers verloren geht b.z.w. in Wärme verwandelt
wird.
Aufgabe 2:
a) Wir wenden die allgemeine Bernoulli- Gleichung an:
Auf unsrere Aufgabe angewendet, folgt:
Hierbei ist 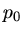 der äußere Luftdruck, der oben und unten am Gefäß derselbe ist,
der äußere Luftdruck, der oben und unten am Gefäß derselbe ist, 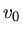 ist die Senkgeschwindigkeit der
Wasseroberfläche,
ist die Senkgeschwindigkeit der
Wasseroberfläche, 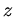 die Höhe der Wasseroberfläche über der unteren Öffnung. Daraus erhalten wir eine Beziehung zwischen
die Höhe der Wasseroberfläche über der unteren Öffnung. Daraus erhalten wir eine Beziehung zwischen
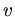 ,
, 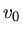 und
und 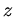 :
:
Eine zweite Beziehung zwischen 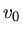 ,
, 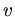 und dem Radius
und dem Radius 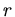 der kreisförmigen Wasserobefläche erhalten wir
aus der Kontinuitätsgleichung
der kreisförmigen Wasserobefläche erhalten wir
aus der Kontinuitätsgleichung
Dann können wir die Geschwindigkeit 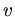 durch
durch 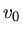 ausdrücken,
ausdrücken,
und in die erste Gleichung einsetzen:
Wir bringen 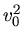 auf die linke Seite und alles andere auf die rechte Seite:
auf die linke Seite und alles andere auf die rechte Seite:
Nach Aufgabenstellung sollte 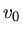 konstant sein, darf also nicht von
konstant sein, darf also nicht von 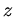 oder
oder 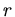 abhängen. Das kann nur erfüllt werden,
wenn
abhängen. Das kann nur erfüllt werden,
wenn
gilt, mit einer Proportionalitätskonstanten 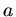 . Dann gilt nämlich
. Dann gilt nämlich
b) Jetzt ist
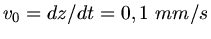 , damit können wir die Konstante
, damit können wir die Konstante 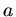 bestimmen.
bestimmen.
Damit die Uhr eine Stunde laufen kann, muß die Anfangshöhe der Wasseroberfläche 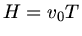 mit
mit
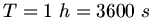 sein, d.h.
sein, d.h. 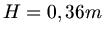 . Wir gehen zurück auf unsere obige Ausgangsformel und schreiben den Radius
. Wir gehen zurück auf unsere obige Ausgangsformel und schreiben den Radius
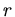 als Funktion von
als Funktion von 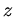 :
:
und setzen 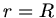 sowie
sowie 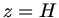 . Dieses ergibt
. Dieses ergibt
Aufgabe 3:
Wir betrachten die Oberflächen der beiden Wassersäulen. Der Gesamtdruck an diesen beiden Punkten muß gleich sein. Dann gilt
wobei 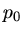 der äußere Luftdruck und
der äußere Luftdruck und 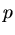 der statische Druck ist.
der statische Druck ist.
Die Geschwindigkeit ist dann
und das Volumen pro Sekunde:
Harm Fesefeldt
2006-01-13