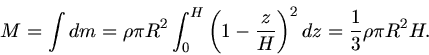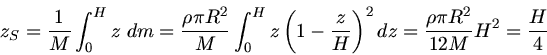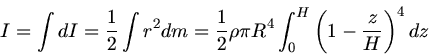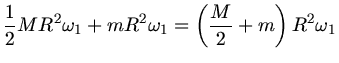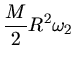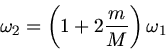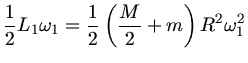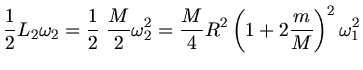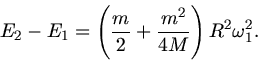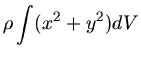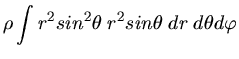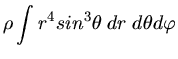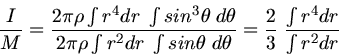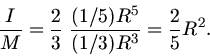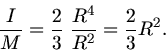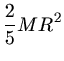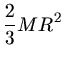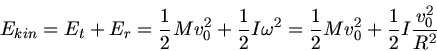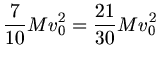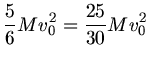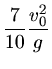Lösungen zur Übung Nr.9
Besprechung: Donnerstag, d. 22. Dezember 2005
Aufgabe 1:
Wir zerlegen den Kreiskegel in dünne Scheiben der Dicke 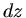 und Radius
und Radius 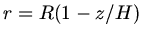 .
. 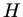 ist die Höhe des Kegels
und
ist die Höhe des Kegels
und 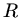 der Radius des Basiskreises (siehe Abbildung).
der Radius des Basiskreises (siehe Abbildung).
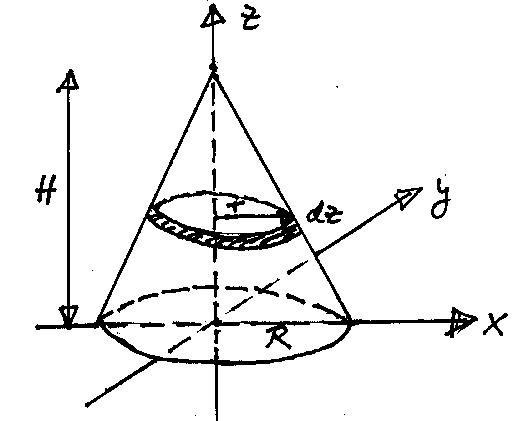
Abbildung 1:
Bezeichnungen beim Kreiskegel
|
Die Masse einer dünnen Kreisscheibe ist dann
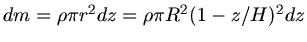 , mit der Massendichte
, mit der Massendichte
 . Die Masse des gesamten Kreiskegels ist dann
. Die Masse des gesamten Kreiskegels ist dann
a) Wir wählen die Symmetrieachse des Kegels als 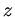 - Achse. Dann liegen aus Symmetriegründen die
- Achse. Dann liegen aus Symmetriegründen die 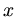 - und
- und 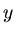 - Koordinaten
des Schwerpunktes bei
- Koordinaten
des Schwerpunktes bei 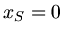 und
und 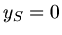 . Für die
. Für die 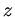 - Koordinate folgt nach Definition
- Koordinate folgt nach Definition
b) Das Trägheitsmoment einer Kreisscheibe ist nach Skript
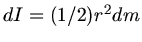 . Integration von
. Integration von 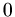 bis
bis 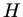 ergibt:
ergibt:
Hierbei haben wir die Ausdrücke für 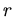 und
und 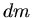 am Anfang der Lösung benutzt. Auswertung des Integrals führt auf
am Anfang der Lösung benutzt. Auswertung des Integrals führt auf
Aufgabe 2:
Die Drehimpulse 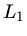 vorher und
vorher und 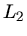 nachher sind
nachher sind
Drehimpulserhaltung verlangt 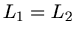 . Daraus folgt
. Daraus folgt
Die Winkelgeschwindigkeit vergrößert sich also.
b) Für die Energien gilt entsprechend:
Die Zunahme der Energie ist
c) Diese Energie muss vom Ingenieur aufgebracht werden, indem er gegen die Zentrifugalkraft Arbeit leistet.
Aufgabe 3:
a) Trägheitsmomente werden allgemein durch eine Formel
dargestellt, wobei 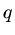 ein numerischer Faktor und
ein numerischer Faktor und 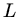 eine charakteristische Länge des Körpers ist.
Daher gilt auch
eine charakteristische Länge des Körpers ist.
Daher gilt auch
Wir betrachten allgemein eine Kugel mit Wandstärke
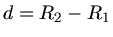 . Die Rotationsachse gehen durch den Mittelpunkt
der Kugel, wir wählen sie als
. Die Rotationsachse gehen durch den Mittelpunkt
der Kugel, wir wählen sie als 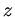 - Achse (siehe Abbildung).
- Achse (siehe Abbildung).
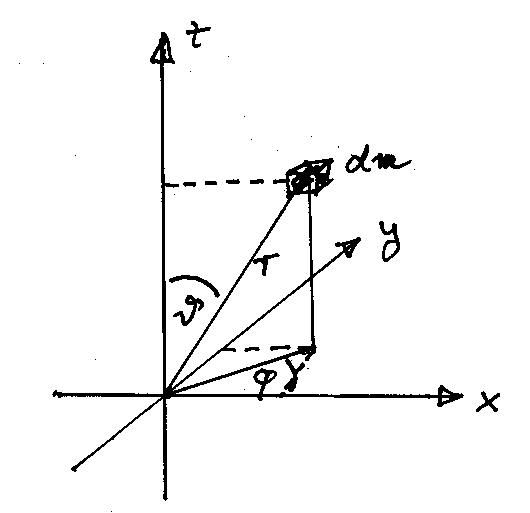
Abbildung 2:
Kugelkoordinaten
|
Dann können wir für die Massse
schreiben. Für das Trägheitsmoment erhalten wir ähnlich:
Das Verhältnis ist allgemein
Für eine Vollkugel setzen wir die Integrationsgrenzen 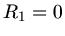 und
und 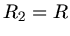 und erhalten
und erhalten
Bei der Hohlkugel ist
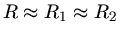 und daher
und daher
Wir fassen zusammen:
b) Die Geschwindigkeit beider Kugeln ist am Anfang gleich, und zwar 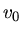 , die kinetische Energie ist aber
verschieden:
, die kinetische Energie ist aber
verschieden:
Im letzten Schritt haben wir
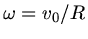 benutzt. Wir setzen die Werte für
benutzt. Wir setzen die Werte für 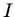 und erhalten
und erhalten
Diese Energie wird in potentielle Energie umgesetzt,
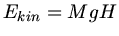 , daher
, daher
Harm Fesefeldt
2006-01-10