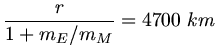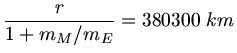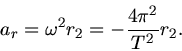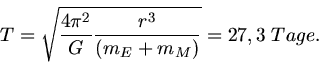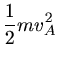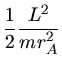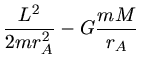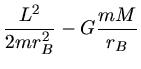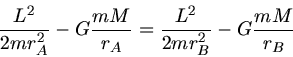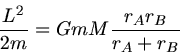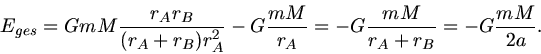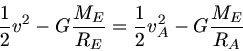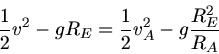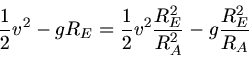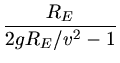Lösungen zur Übung Nr.8
Besprechung: Donnerstag, d. 15. Dezember 2005
Aufgabe 1:
a) Erde und Mond bewegen sich auf Kreisbahnen um ihren gemeinsamen Schwerpunkt, daher gilt
Daraus folgern wir
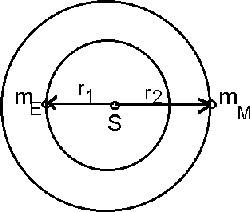
Abbildung 1:
Erde- Mond System mit Schwerpunkt S.
 |
Das Bewegungszentrum liegt also noch innerhalb der Erdkugel. Diese 380000 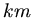 werden üblicherweise als
Abstand von Erde und Mond angegeben. Das ist ersichtlich nicht ganz richtig, es ist genau genommen der Bahnradius des
Mondes.
werden üblicherweise als
Abstand von Erde und Mond angegeben. Das ist ersichtlich nicht ganz richtig, es ist genau genommen der Bahnradius des
Mondes.
b) Die Umlaufdauer des Mondes wird über die Bewegungsgleichung
bestimmt. Hier muss man jetzt aufpassen. Im Gravitationsgesetz steht der Abstand
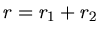 zwischen Mond und
Erde, während die Radialbeschleunigung des Mondes mit dem Bahnradius
zwischen Mond und
Erde, während die Radialbeschleunigung des Mondes mit dem Bahnradius 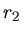 beschrieben werden muss:
beschrieben werden muss:
Damit findet man
Aufgabe 2:
Wir betrachten die Punkte 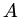 und
und 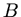 in der folgenden Skizze.
in der folgenden Skizze.
Abbildung 2:
Ellipsenbahn eines Planeten mit Sonne S.
 |
In diesen Punkten ist der Drehimpuls durch
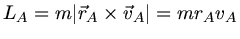 und
und
 gegeben, da der Ortsvektor in diesen beiden
Punkten senkrecht zur Geschwindigkeit ist.
Dann ist mit
gegeben, da der Ortsvektor in diesen beiden
Punkten senkrecht zur Geschwindigkeit ist.
Dann ist mit
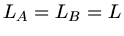
und mit Formel (3), Skript Teil 7, Seite 5 auch
Da neben dem Drehimpuls auch die Gesamtenergie konstant ist, folgt
Damit können wir jetzt den Drehimpuls berechnen:
Diesen Ausdruck setzen wir jetzt in die Formel für die Gesamtenergie z.B. im Punkte 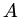 ein:
ein:
Aufgabe 3:
Diese Aufgabe ist sehr ähnlich der Aufgabe 2.
Die Bahnen beider Satelliten werden durch Ellipsenbahnen beschrieben. Die Anfangsgeschwindigkeiten sind bei Abschuss am
Äquator durch
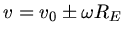 beschrieben, mit der Kreisfrequenz
beschrieben, mit der Kreisfrequenz 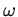 der Eigenrotation der Erde.
Den größten Abstand
von der Erde erreicht der Satellit im Schnittpunkt der Bahn mit der großen Halbachse. Die Geschwindigkeit im Punkte
der Eigenrotation der Erde.
Den größten Abstand
von der Erde erreicht der Satellit im Schnittpunkt der Bahn mit der großen Halbachse. Die Geschwindigkeit im Punkte 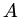 sei
sei 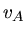 , dann gilt wegen Drehimpulserhaltung
, dann gilt wegen Drehimpulserhaltung
Abbildung 3:
Bahnen von Satelliten der Erde
 |
Erhaltung der Gesamtenergie verlangt:
Wir ersetzen
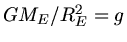 durch die Schwerebeschleunigung auf der Erdoberfläche, dann erhalten wir
durch die Schwerebeschleunigung auf der Erdoberfläche, dann erhalten wir
Wir übernehmen 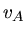 aus der Formel für die Drehimpuls- Erhaltung und erhalten:
aus der Formel für die Drehimpuls- Erhaltung und erhalten:
Damit erhalten wir die quadratische Gleichung für den Abstand 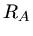 :
:
mit den zwei Lösungen:
Die erste Lösung ist der Abschußort, der zweite Lösung ist der maximale Abstand.
Wir setzen jetzt noch die Anfangsgeschwindigkeiten
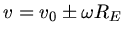 ein und erhalten für die beiden
Satelliten die Maximalabstände
ein und erhalten für die beiden
Satelliten die Maximalabstände
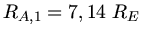 und
und
 . Man sieht, daß die Eigenrotation der Erde einen großen
Einfluss auf die Ellipsenbahn hat.
. Man sieht, daß die Eigenrotation der Erde einen großen
Einfluss auf die Ellipsenbahn hat.
b) Der kritische Satellit ist der mit der größeren Geschwindigkeit. Der Maximalabstand vom Erdmittelpunkt wird
unendlich, wenn der Nenner in der Formel von Teil a) Null wird, d.h.
oder
mit
 erhalten wir
erhalten wir
Der zweite Satellit verschwindet dagegen erst bei
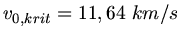 im Weltall. Die kritische Geschwindigkeit
ohne Erdrotation ist
im Weltall. Die kritische Geschwindigkeit
ohne Erdrotation ist 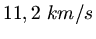 .
.
Harm Fesefeldt
2005-12-16