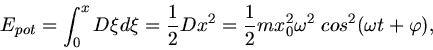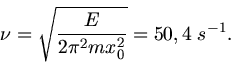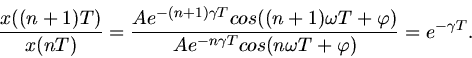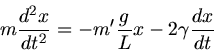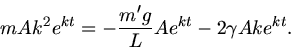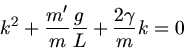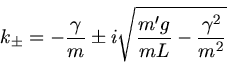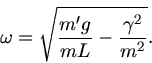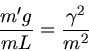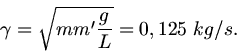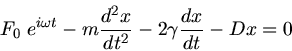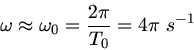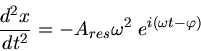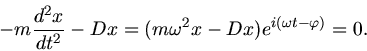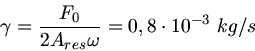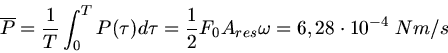Lösungen zur Übung Nr.7
Besprechung: Donnerstag, d. 8. Dezember 2005
Aufgabe 1:
Wir müssen die Schwingungsfrequenz als Funktion der Gesamtenergie darstellen.
Die Gesamtenergie ist immer die Summe aus kinetischer und potentieller Energie,
Die allgemeine Lösung der Schwingungsgleichung ohne Dämpfung ist
Die Geschwindigkeit hierzu ist
Für die kinetische Energie erhalten wir:
Für die potentielle Energie erhalten wir
mit der Eigenfreqeunz
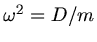 . Die Gesamtenergie ist dann
. Die Gesamtenergie ist dann
mit
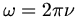 . Für die gesuchte Frequenz erhalten wir hieraus:
. Für die gesuchte Frequenz erhalten wir hieraus:
Aufgabe 2:
Die gedämpfte Schwingung stellen wir dar mit einer Cosinus - Funktion, deren Amplitude exponentiell abnimmt.
Diese Lösung erfüllt die Schwingungsgleichung (bitte nachrechnen). Daher folgt für das Verhältnis
der Auslenkungen bei zwei aufeinanderfolgenden Schwingungen:
Nach Aufgabenstellung
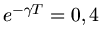 . Daher
. Daher
Die Kreisfrequenz der ungedämpften Schwingung ist
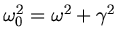 , die Frequenz also
, die Frequenz also
Aufgabe 3:
a) Wir wollen diese Aufgabe nutzen, um den allgemeinen Lösungsansatz der gedämpften Schwingungsgleichung mit komplexen Zahlen
zu lösen. Die Bewegungsgleichung lautet in diesem Fall
Man beachte, daß 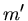 die um den Auftrieb verringerte Masse des Pendelkörpers ist:
die um den Auftrieb verringerte Masse des Pendelkörpers ist:
Wir versuchen den Lösungsansatz
Hierbei haben wir die Phase  gesetzt. Dieses ist nichts weiter als die Wahl des Zeit- Nullpunktes.
Dann folgen die Ableitungen
gesetzt. Dieses ist nichts weiter als die Wahl des Zeit- Nullpunktes.
Dann folgen die Ableitungen
Dieses setzen wir in die Schwingungsgleichung ein und erhalten die Bedingung für 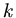 :
:
Nach Wegkürzen von 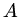 und
und 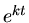 bleibt
bleibt
mit den 2 Lösungen:
Die 2 Lösungen der Schwingungsgleichung sind also
mit
Physikalisch interessant sind nur die Realteile der Lösungen:
Da
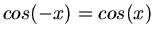 ist, sind beide Lösungen physikalisch identisch gleich.
Für die Schwingungsdauer erhalten wir:
ist, sind beide Lösungen physikalisch identisch gleich.
Für die Schwingungsdauer erhalten wir:
b) Der aperiodische Grenzfall wird erreicht für  , daher
, daher
oder
,5cm
Aufgabe 4:
Die Schwerkraft erzeugt eine konstante Auslenkung der Feder, verschiebt also lediglich den Nullpunkt der Auslenkung.
Die Bewegungsgleichung ist
Im Resonanzfall gilt bei schwacher Dämpfung
Wir versuchen wieder einen komplexen Lösungsansatz,
wobei  der Phasenwinkel zwischen der treibenden Kraft und der Schwingung ist. Die zweite Ableitung lautet
der Phasenwinkel zwischen der treibenden Kraft und der Schwingung ist. Die zweite Ableitung lautet
und daher (beachte
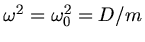 )
)
Im Resonanzfall ist also bei schwacher Dämpfung die äußere Kraft gleich der Reibungskraft:
Diese Gleichung spalten wir jetzt in einen Realteil und Imaginärteil auf,
Aus der zweiten Gleichung folgern wir, daß
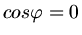 sein muß, also
sein muß, also
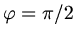 . Damit wird
. Damit wird
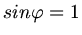 und daher
folgt aus der ersten Gleichung:
und daher
folgt aus der ersten Gleichung:
oder
b) Die Leistung ist
Der Realteil der treibenden Kraft ist
Die Geschwindigkeit ist
mit Realteil (beachte
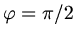 )
)
Die mittlere Leistung ist
c) Im Resonanzfall besteht zwischen Geschwindigkeit  und der äußeren Kraft
und der äußeren Kraft 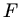 kein Phasenunterschied. Die Amplitude
der Geschwindigkeit hat ein Maximum. Daher hat auch die Arbeit, die während einer Periode von der äußeren Kraft
geleistet wird, ein Maximum.
kein Phasenunterschied. Die Amplitude
der Geschwindigkeit hat ein Maximum. Daher hat auch die Arbeit, die während einer Periode von der äußeren Kraft
geleistet wird, ein Maximum.
Animation
Alle Aufgaben dieser Übung können Sie mit dem folgenden
Java- Applet visuell nachvollziehen. Eine Bedienungsanleitung finden Sie
beim Klicken auf den Doc- Button.
Harm Fesefeldt
2005-12-09