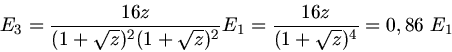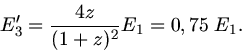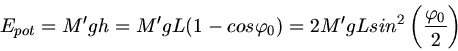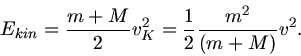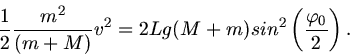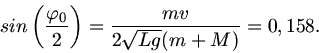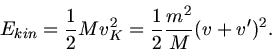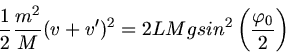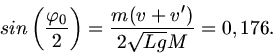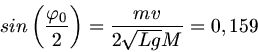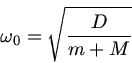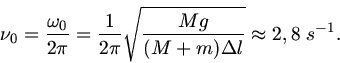Lösungen zur Übung Nr.6
Besprechung: Donnerstag, d. 1. Dezember 2005
Aufgabe 1:
Beim zentralen elastischen Stoß ist die Geschwindigkeit der Kugeln nach dem Stoß:
Abbildung:
Elastischer Stoß dreier Kugeln auf einer Geraden
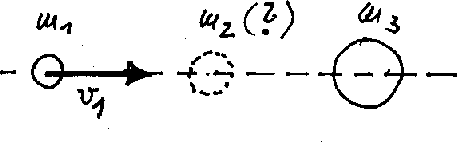 |
Die Energie 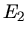 der zweiten Kugel ist also
der zweiten Kugel ist also
Im letzten Schritte haben wir noch die Abkürzung
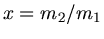 eingeführt. Entsprechend gilt beim Stoß der zweiten mit
der dritten Kugel
eingeführt. Entsprechend gilt beim Stoß der zweiten mit
der dritten Kugel
mit
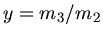 . Daher ist auch
. Daher ist auch
Weiterhin setzen wir
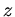 ist also konstant. Die Energie der dritten Kugel können wir jetzt als Funktion der Variablen
ist also konstant. Die Energie der dritten Kugel können wir jetzt als Funktion der Variablen
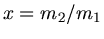 und der
Konstanten
und der
Konstanten 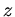 schreiben:
schreiben:
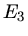 wird maximal, wenn der Nenner minimal wird. Daher suchen wir nach dem
wird maximal, wenn der Nenner minimal wird. Daher suchen wir nach dem 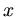 , bei dem
, bei dem
wird. Die Auswertung dieser Extremalaufgabe ergibt
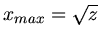 (bitte nachrechnen) oder
(bitte nachrechnen) oder
Die Energie der dritten Kugel berechnet sich zu:
b) Wir nehmen jetzt die zweite Kugel weg und berechnen die Energie der dritten Kugel beim direkten elastischen Stoß
der ersten mit der dritten Kugel. Hierzu verwenden wir eine oben bereits abgeleitete Formel
Man sieht also, daß der Energieübertrag von der ersten auf die dritte Kugel größer wird, wenn man eine Kugel mit der
Masse
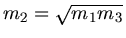 dazwischen schaltet. Entsprechend kann man mehrere Kugeln mit Massen
dazwischen schaltet. Entsprechend kann man mehrere Kugeln mit Massen
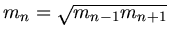 einfügen. Man kommt dann zu einer Kugelpyramide, wie sie auch in der Vorlesung als
Experiment gezeigt worden ist.
einfügen. Man kommt dann zu einer Kugelpyramide, wie sie auch in der Vorlesung als
Experiment gezeigt worden ist.
Aufgabe 2:
Allgemein gilt, wenn 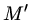 die Masse des Pendelkörpers ist, für die potentielle Energie beim Maximalausschlag mit dem
Winkel
die Masse des Pendelkörpers ist, für die potentielle Energie beim Maximalausschlag mit dem
Winkel 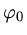 :
:
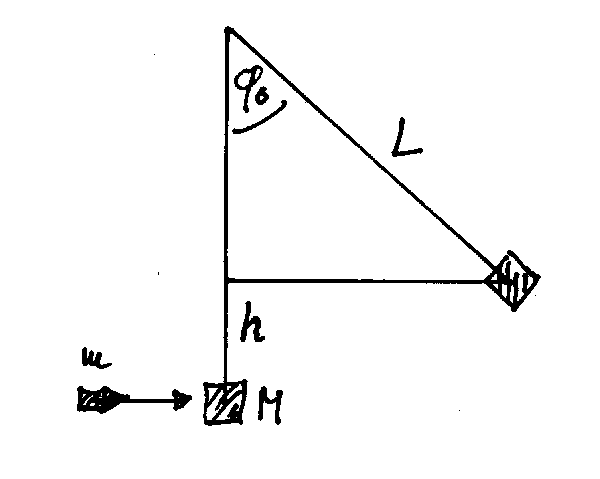
Abbildung 2:
Bezeichnungen beim ballistischen Pendel
|
Wir machen hier also nicht die Approximation
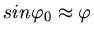 , da wir über die Größe der
Auslenkung nichts wissen. Die Masse
, da wir über die Größe der
Auslenkung nichts wissen. Die Masse 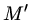 ist bei den drei Fällen a), b) und c) verschieden, nämlich einmal
ist bei den drei Fällen a), b) und c) verschieden, nämlich einmal
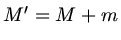 (Teil a) und
(Teil a) und 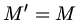 (Teil b und c). Diese potentielle Energie muß gleich der kinetischen Energie des
Pendelkörpers nach dem Aufprall der Geschosskugel sein. Für die Berechnung dieser kinetischen Energie können wir aber nicht den
Energiesatz verwenden, da der Stoß der Kugel in allen drei Fällen inelastisch ist und ein Teil der Energie durch Reibung
verloren geht. Hier können wir nur den Impulssatz anwenden.
(Teil b und c). Diese potentielle Energie muß gleich der kinetischen Energie des
Pendelkörpers nach dem Aufprall der Geschosskugel sein. Für die Berechnung dieser kinetischen Energie können wir aber nicht den
Energiesatz verwenden, da der Stoß der Kugel in allen drei Fällen inelastisch ist und ein Teil der Energie durch Reibung
verloren geht. Hier können wir nur den Impulssatz anwenden.
a) Hier ist wegen Impulserhaltung
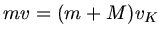 , wobei also
, wobei also 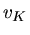 die Geschwindigkeit des Pendelkörpers am Anfang seiner
Bewegung ist. Damit wird die kinetische Energie
die Geschwindigkeit des Pendelkörpers am Anfang seiner
Bewegung ist. Damit wird die kinetische Energie
mit der Geschwindigkeit 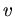 der Kugel vor dem Stoß. In die Formel für die potentielle Energie müssen wir
der Kugel vor dem Stoß. In die Formel für die potentielle Energie müssen wir
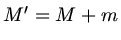 einsetzen, daher
einsetzen, daher
Augelöst nach 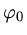 folgt:
folgt:
oder
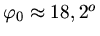 .
.
b) In diesem Fall fordert die Impulserhaltung
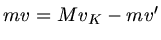 , da die Kugel nach dem Stoss mit der kleineren
Geschwindigkeit
, da die Kugel nach dem Stoss mit der kleineren
Geschwindigkeit 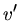 zurückfliegt. Die kinetische Energie des Pendelkörpers direkt nach dem Aufprall ist also
zurückfliegt. Die kinetische Energie des Pendelkörpers direkt nach dem Aufprall ist also
In die Formel für die potentielle Energie ist diesmal 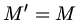 zu setzen, daher
zu setzen, daher
Daraus folgt
oder
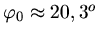 .
.
c) Dieses ist natürlich ein Spezialfall von Teil b) mit 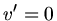 . Daher
. Daher
oder
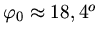 .
.
Aufgabe 3:
Da sich das Seil elastisch ausdehnt, wirkt es wie eine Feder. Die Federkonstante berechnen wir aus
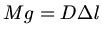 ,
wobei also
,
wobei also 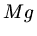 die Kraft und
die Kraft und 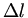 die Auslenkung ist:
die Auslenkung ist:
Die Kreisfrequenz der Schwingung ist
und die Frequenz ist
Harm Fesefeldt
2005-12-03
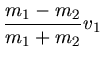
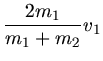
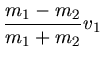
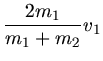
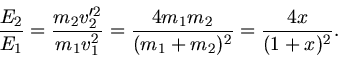
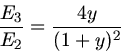
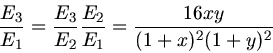
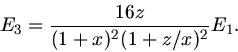
![\begin{displaymath}
\frac{dN}{dx} = \frac{d}{dx} \left[ (1 + x)^{2} (1 + \frac{z}{x})^{2} \right] = 0
\end{displaymath}](img18.gif)