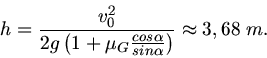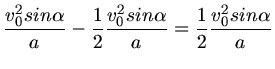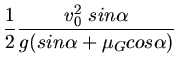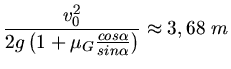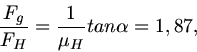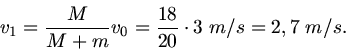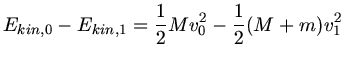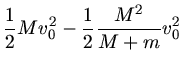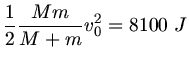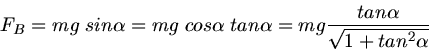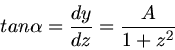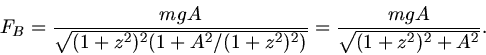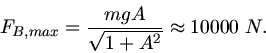Lösungen zur Übung Nr.5
Besprechung: Donnerstag, d. 24. November 2005
Aufgabe 1:
Der erste Teil der Aufgabe kann auf zwei verschiedenen Lösungswegen bearbeitet werden
a) 1. Lösungsweg.
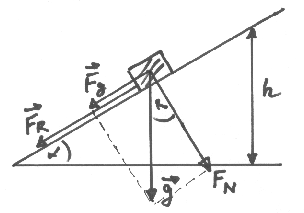
Die Auflagekraft ist
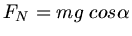 , die Gleitreibungskraft daher
, die Gleitreibungskraft daher
Auf dem Weg
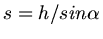 wird daher die Arbeit
wird daher die Arbeit
verbraten. Der Energiesatz lautet hiermit
Aufgelöst nach 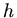 ergibt:
ergibt:
Abbildung 1:
Klotz auf der schiefen Ebene
 |
2. Lösungsweg:
Der zweite Lösungsweg ist etwas komplizierter und geht von der Bewegungsgleichung auf der schiefen Ebene aus:
Mit
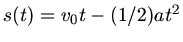 und
und
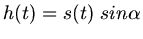 folgt
folgt
Die maximale Höhe wird erreicht, wenn 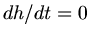 wird.
wird.
Die maximale Höhe wird also nach der Zeit
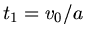 erreicht. Einsetzen in die Formel für
erreicht. Einsetzen in die Formel für 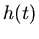 ergibt
ergibt
b) Das Verhältnis der rücktreibenden Schwerkraft
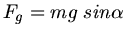 zur Haftreibungskraft
zur Haftreibungskraft
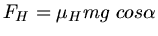 ist
ist
und damit größer 1. Daher gleitet der Klotz die Ebene wieder herunter.
Aufgabe 2:
a) Dieses ist ein inelastischer Vorgang, d.h. man kann nur den Impulssatz, nicht jedoch den Energiesatz
anwenden:
wobei
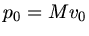 der Impuls des Wagens ohne Sand und
der Impuls des Wagens ohne Sand und
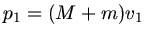 der Impuls des Wagens mit Sand ist.
Ausserdem ist
der Impuls des Wagens mit Sand ist.
Ausserdem ist 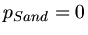 . Also gilt
. Also gilt 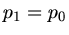 oder
oder
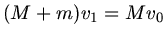 . Aufgelöst nach
. Aufgelöst nach 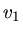 folgt:
folgt:
b) Die Energiedifferenz ist
Diese Energie geht in Reibungswärme verloren, wenn der Sand sich auf dem Boden des Wagens reibt. Der Sand muß ja in
Fahrtrichtung berschleunigt werden.
c) Nach Ausschütten des Sandes ändert sich die Geschwindigkeit des Wagens nicht. Der Sand nimmt seinen Impuls mit.
oder
Die Geschwindigkeit des Wagens bleibt
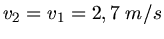 .
.
Aufgabe 3:
a) Die beschleunigende Kraft ist immer längs der Bahn gerichtet. Mit den Bezeichnungen der Skizze gilt
Abbildung 2:
Skizze der Strassenprofiels
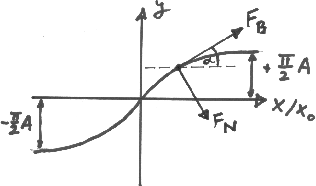 |
In unsrerem Fall ist 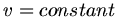 , daher
, daher  . Um
. Um 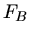 als Funktion von
als Funktion von 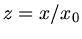 darzustellen, sind einige
mathematische Manipulationen notwendig. Zunächst schreiben wir
darzustellen, sind einige
mathematische Manipulationen notwendig. Zunächst schreiben wir
Hiermit haben wir die Steigung
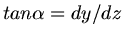 der Bahnkurve ins Spiel gebracht. Mit
der Bahnkurve ins Spiel gebracht. Mit
folgt dann
Um die maximale Kraft zu bestimmen, könnte man aus der Ableitung eine Extremalbedingung herleiten. Das ist in diesem
Fall aber nicht nötig. Man sieht sofort, daß 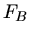 maximal wird, wenn der Nenner minimal wird, also für
maximal wird, wenn der Nenner minimal wird, also für 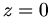 .
Die Kraft in diesem Punkt ist
.
Die Kraft in diesem Punkt ist
b) Auch die Arbeit könnte man umständlicherweise über ein Integral bestimmen,
Einfacher geht es natürlich, wenn man die Hubarbeit bestimmt:
Harm Fesefeldt
2005-11-25